hash

视频

今天的讲解主要分为两部分：

1. 模拟散列表
2. 字符串哈希

1、模拟散列表

散，在英文中的意思是unordered，散列表，就是离散化过的列表（其实是hash）。
个人觉得hash的思路和离散化的思路很像。

hash的思路

就是将一个数字或一个字符串hash成一个比较小的数。

hash造成的问题

我们一般会通过把一个数字取模对这个数字进行hash，取模值一般为200003。
但是，我们就算开再大的数进行hash，也有可能两个数产生冲突——它们的hash值一样。
那这个咱们怎么处理呢？

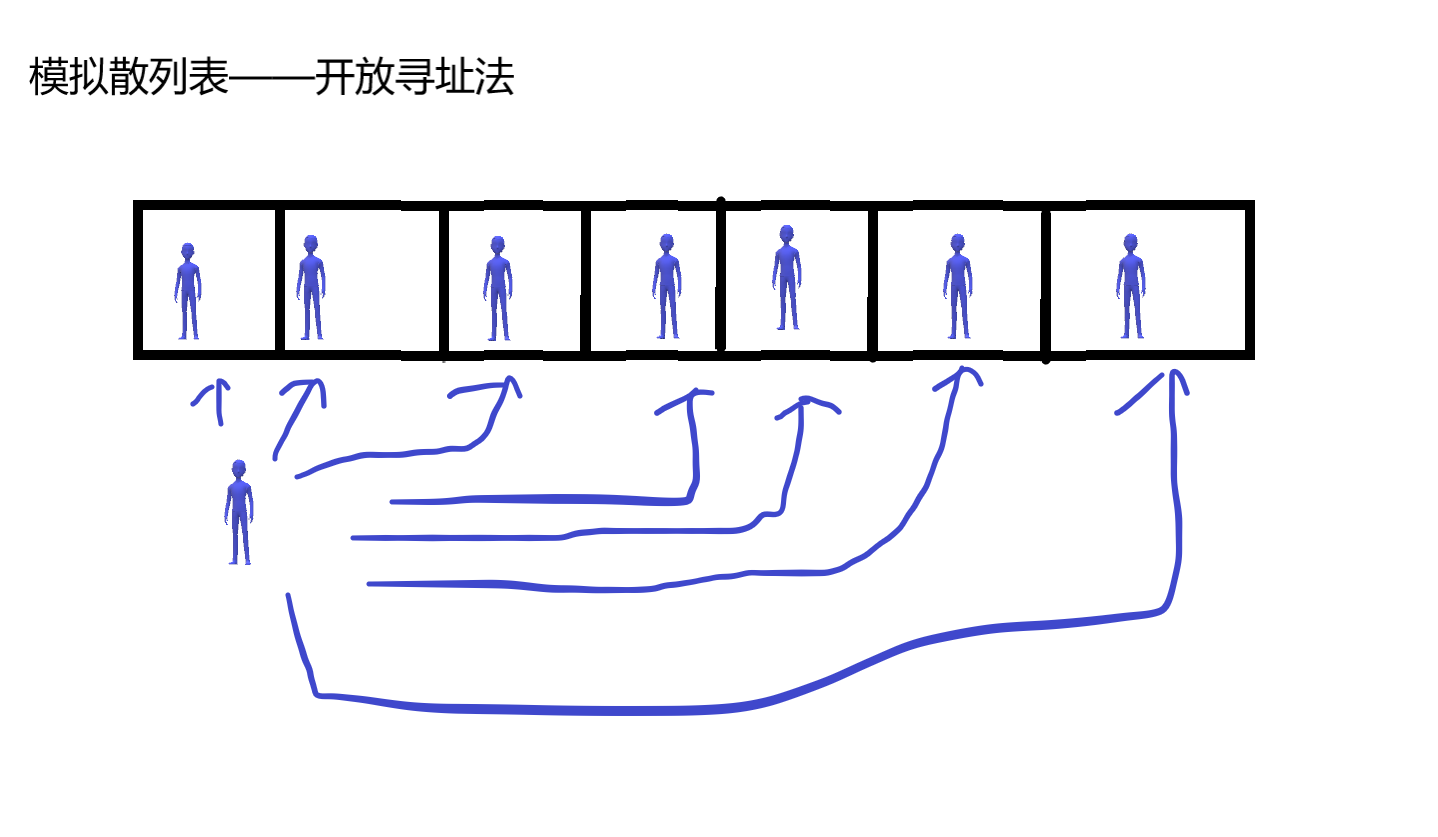
处理冲突——开发寻址法

我们可以把整个hash数组想成一个公共厕所（wc）。
每次我们从当前数的hash值开死开始，有人就继续康。
走到结尾就从头康，反正肯定有位子。。。。。。。。
那我们就可以实现了。
前提是我们需要给每个数赋值为0x3f，这样就可以康康这个位子有没有人了，其次这个位子上海不能是x。
那代码就应该很简单了。

hash开放寻址法代码

int find(int x)
{
    int t = (x % N + N) % N;
    while(h[t] != INF && h[t] != x)
    {
        t ++;
        if(t == N) t = 0;
    }
    return t;
}

这里简单讲解一下为什么hash值要进行膜N加N再膜N。
我们是为了处理负数。

1、如果这个数是正数。
比如17，去膜19，首先先膜一下19，答案是17。
再加上19,17 + 19 = 36（好像没算错），再膜上19还是17。
2、如果不是正数。
····2-1、是0
····0 % 19 = 0， 0 + 19 = 19，19 % 19 = 0。
····无语。。。。
····2-2、是负数
····-7 % 19 = -7（c++特性，真无语）
····-7 + 19 = 12
····12 % 19 = 12

大家都明白了吗？

处理冲突——拉链法

既然我们会有冲突，那我们就可以在每个数值上写一个单链表，然后每次插入这个数就行了。
太弱了。。。。
看下图吧。

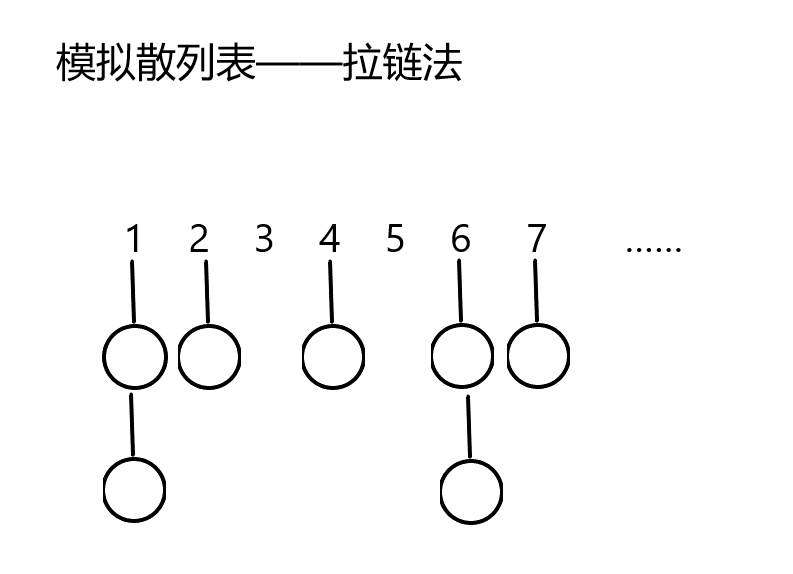
这大家就明白了，这不就是个单链表吗！
来接下来看看题就知道这玩意有多弱了。
拉链法trl
好这题中有这么几个操作。
1. 插入。
2. 判断是否存在于集合中。

我们之前已经学过了图论，今天可以应用一下这些知识。
比如图论中插入操作和遍历操作。
插入：

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

遍历：

for(int i = h[start]; i != -1; i = ne[i])
{
    int j = e[i];
    //blahblahblah
}

那我们就可以把这些知识应用到拉链法上。
废话少说上代码。
hash的方式也是取模，跟开放寻址法一样，这里不多说。
首先是把这个数插进散列表。

void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

接着是判断在不在，挨个枚举。

bool find(int x)
{
    int k = (x % N + N) % N;
    for(int i = h[k]; i != -1; i = ne[i])
    {
        if(e[i] == x)
        {
            return true;
        }
    }
    return false;
}

弱爆了对吧。
然后是这道题的两种不同代码：
1、开放寻址法

#include<bits/stdc++.h>
using namespace std;
const int N = 200003, INF = 0x3f3f3f3f;
int h[N];
int find(int x)
{
    int t = (x % N + N) % N;
    while(h[t] != INF && h[t] != x)
    {
        t ++;
        if(t == N) t = 0;
    }
    return t;
}
int main()
{
    int n;
    cin >> n;
    memset(h, 0x3f, sizeof h);
    while(n --)
    {
        char op;
        cin >> op;
        int x;
        cin >> x;
        int k = find(x);
        if(op == 'I') h[k] = x;
        else 
        {
            if(h[k] == INF) puts("No");
            else puts("Yes");
        }
    }
}

2、拉链法

#include <cstring>
#include <iostream>

using namespace std;

const int N = 100003;

int h[N], e[N], ne[N], idx;

void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

bool find(int x)
{
    int k = (x % N + N) % N;
    for(int i = h[k]; i != -1; i = ne[i])
    {
        if(e[i] == x)
        {
            return true;
        }
    }
    return false;
}

int main()
{
    int n;
    scanf("%d", &n);

    memset(h, -1, sizeof h);

    while (n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        if (*op == 'I') insert(x);
        else
        {
            if (find(x)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

字符串哈希

字符串哈希就是哈希一个字符串。
原理很简单，过程很复杂。
我们先预处理出每个前缀的哈希值。
就像前缀和那样。
最后再拼凑成一个子串的哈希值。
最后对比两个哈希值就行了。
那我们如何hash呢？
我们可以把这个字符串看成一个P进制的数。
然后我们定义一个P数组来存每一位的幂即可。
这应该就很简单了吧。

for(int i = 1; i <= n; i ++)
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;
}

然后还有一个公式，叫做如何求出一个子串的哈希值。
证明大家去看基础课视频吧……反正很好背我这个xxs就直接背下来了，数学底子不行啊！
具体自求子串公式：

unsigned long long int f(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

好了那完整代码就应该一目了然了。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, P = 131;
#define u unsigned long long 
u n, m, h[N], p[N];
char str[N];
u f(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}
int main()
{
    cin >> n >> m >> str + 1;p[0] = 1;
    for(int i = 1; i <= n; i ++)
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
    while(m --)
    {
        u a, b,c, d;
        cin >> a >> b >> c >> d;
        if(f(a, b) == f(c, d)) puts("Yes");
        else puts("No");
    }
    return 0;
}

数太大了所以要用这个

unsigned long long

有人可能问我怎么背……
我：自己死背，我这个蒟蒻就是这么背的………………
好了今天的分享就到这里了。
没有制作幻灯片并且没有备课这两件事对大家说一声：

对不起！

那我还是老规矩留一个作业：

兔子与兔子

提示一下要用前缀和哦

好了今天的分享就到这里了。

这里是我的全部分享！

hhh好久没更新了，现在不叫30天计划了，叫cht讲算法了。

现在不按自己的学习顺序讲了，而是赶紧讲完基础课去搞提高课hhh

这里愿所有Oler都能早日学完所有算法！AKIOI！（当然我这辈子也别想了，我这么弱）

好了那就

bye~

附：小公告一枚

以前讲过两期Windows系统编程（DEVC++）
1
2
现在觉得抽时间给大家更新进阶课。
学完前两个基础课的同学可以学习了。
看完进阶课基本就可以编一个小型的工程了。
现在正在编一个小游戏。
以及最近编程时间比较少，
一是开学了，
二是蓝桥杯省赛要开始了。
所以更分享的时间比较少。
大家谅解一下。
感谢大家这么久对我的支持
谢谢了。
好了那就真的再见了。
bye~
（hhh凑个整，300行）