自存！！！可看，勿喷QWQ

平衡树 Treap -> tree + heap
BST(二叉搜索树) + 堆
在BST中，数可能会退化成链，在平衡树中，用堆的思想判断，旋转来调整

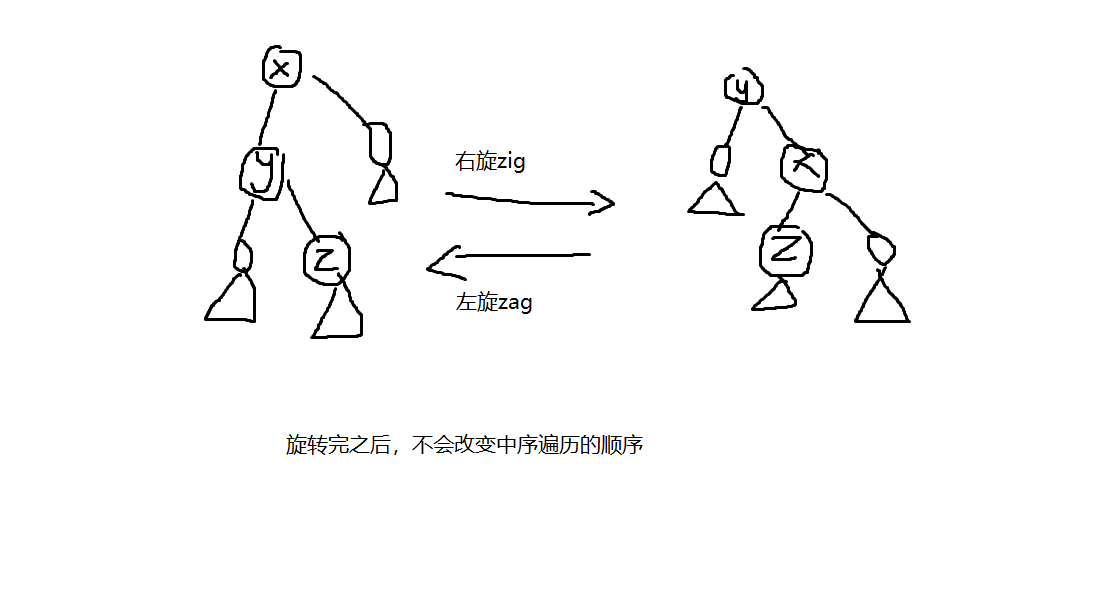
代码：

void zig(int &p)
{
    int q = tr[p].l;
    tr[p].l = tr[q].r;
    tr[q].r = p;
    p = q;
    pushup(tr[p].r);
    pushup(p);
}

void zag(int &p)
{
    int q = tr[p].r;
    tr[p].r = tr[q].l;
    tr[q].l = p;
    p = q;
    pushup(tr[p].l);
    pushup(p);
}

Treap定义：

Struct Treap
{
    int l, r;
    int key, val;
    int cnt,size;
}tree[N];
其中key是点权
val是一个随机的数，满足一个节点的val值大于等于左儿子和右儿子的val
cnt表示这个数有多少
size表示子树有多少个数（有算重复）

构建（会有两个哨兵，以防越界）：

void pushup(int p)
{
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}

int get_node(int key) //创建节点,返回编号
{
    tr[ ++ idx ].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].size = 1;
    return idx;
}

void build() //建树
{
    get_node(-INF);
    get_node(INF);
    root = 1;
    tr[1].r = 2;
    pushup(root);
    if (tr[1].val < tr[2].val) zag(root);
}

操作（BST的操作）：

①插入一个数：

void insert(int &p, int key)
{
    if (!p) p = get_node(key);
    else if (tr[p].key == key) tr[p].cnt ++ ;
    else if (tr[p].key > key)
    {
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);
    }
    else
    {
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);
    }
    pushup(p);
}

②删除一个数：

void remove(int &p, int key)
{
    if (!p) return;
    if (tr[p].key == key)
    {
        if (tr[p].cnt > 1) tr[p].cnt -- ;
        else if (tr[p].l || tr[p].r)
        {
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)
            {
                zig(p);
                remove(tr[p].r, key);
            }
            else
            {
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0;
    }
    else if (tr[p].key > key) remove(tr[p].l, key);
    else remove(tr[p].r, key);
    pushup(p);
}

③找小于x最大的数/大于x最小的数

int get_prev(int &p, int key)//前驱
{
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}

int get_next(int &p, int key)//后继
{
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

④求某个数的排名/求排名是x的数

注意：因为有哨兵，所以求排名后要减1，给排名求数时排名要加1

int get_rank_by_key(int &p, int key)//求排名
{
    if (!p) return 0;
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}

int get_key_by_rank(int &p, int rank)//求排名对应的数
{
    if (!p) return INF;
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}

模板题

1. 插入数值 x
2. 删除数值 x (若有多个相同的数，应只删除一个)。
3. 查询数值 x 的排名(若有多个相同的数，应输出最小的排名)。
4. 查询排名为 x 的数值。
5. 求数值 x 的前驱(前驱定义为小于 x 的最大的数)。
6. 求数值 x 的后继(后继定义为大于 x 的最小的数)。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdio>

using namespace std;

const int N = 100010, INF = 1e8;

int n;
struct Treap
{
    int l, r;
    int key, val;
    int cnt; // 这个数有多少（重复的数在一个节点上）
    int size; // 子树有多少（有算重复数）
}tr[N];

int root, idx;

void pushup(int p)
{
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}

int get_node(int key) //创建节点,返回编号
{
    tr[ ++ idx ].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].size = 1;
    return idx;
}

void zig(int &p)//右旋
{
    int q = tr[p].l;
    tr[p].l = tr[q].r;
    tr[q].r = p;
    p = q;
    pushup(tr[p].r);
    pushup(p);
}

void zag(int &p)//左旋
{
    int q = tr[p].r;
    tr[p].r = tr[q].l;
    tr[q].l = p;
    p = q;
    pushup(tr[p].l);
    pushup(p);
}


void build() //建树
{
    get_node(-INF);
    get_node(INF);
    root = 1;
    tr[1].r = 2;
    pushup(root);
    if (tr[1].val < tr[2].val) zag(root);
}

void insert(int &p, int key)
{
    if (!p) p = get_node(key);
    else if (tr[p].key == key) tr[p].cnt ++ ;
    else if (tr[p].key > key)
    {
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);
    }
    else
    {
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);
    }
    pushup(p);
}

void remove(int &p, int key)
{
    if (!p) return;
    if (tr[p].key == key)
    {
        if (tr[p].cnt > 1) tr[p].cnt -- ;
        else if (tr[p].l || tr[p].r)
        {
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)
            {
                zig(p);
                remove(tr[p].r, key);
            }
            else
            {
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0;
    }
    else if (tr[p].key > key) remove(tr[p].l, key);
    else remove(tr[p].r, key);
    pushup(p);
}

int get_rank_by_key(int &p, int key)
{
    if (!p) return 0;
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}

int get_key_by_rank(int &p, int rank)
{
    if (!p) return INF;
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}

int get_prev(int &p, int key)
{
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}

int get_next(int &p, int key)
{
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main()
{
    build();
    int T;
    cin >> T;
    while (T -- )
    {
        int op, x;
        cin >> op >> x;
        if (op == 1) insert(root, x);
        else if (op == 2) remove(root, x);
        else if (op == 3) cout << get_rank_by_key(root, x) - 1 << endl;
        else if (op == 4) cout << get_key_by_rank(root, x + 1) << endl;
        else if (op == 5) cout << get_prev(root, x) << endl;
        else cout << get_next(root, x) << endl;
    }
    return 0;
}