1.二叉树的性质
性质:
左孩子、右孩子、左子树、右子树;
二叉树第i层(i>=1)最多2i−1个节点;
一个n层满二叉树,共2n−1个节点;
完全二叉树:只在最后一层的最后有缺失编号的满二叉树;
根到节点u的距离为节点u的深度;节点u到到它的叶子节点的距离为节点u的高度;根的高度最大,称为树的高。
二叉树的优势:
(1)访问效率高。一棵有N个节点的平衡二叉树,从根到叶子节点只需log2N步;但不平衡的二叉树,极端情况下会退化成“链”,访问效率会降低。维护二叉树的平衡是高级数据结构的主要任务之一。
(2)很适合整体到局部、局部到整体的操作。如求区间最值、区间和、区间翻转、区间合并、区间分裂等。
(3)基于二叉树的算法容易设计与实现。如DFS、BFS。
2.二叉树的存储结构
(1)动态二叉树。
每次new一个节点,使用完delete。不浪费空间,但需要管理,容易出错。
(2)静态数组存储二叉树。
编码简单,速度快。
用数组实现完全二叉树,左右子节点都不用定义:
总节点个数为k的完全二叉树,编号i>1的节点,父节点i/2;
若2i>k,则节点i没有子节点,若2i+1>k,则节点i没有右子节点;
如果节点i有子节点,那么左子节点是2i,右子节点是2i+1。
(3)多叉树转化为二叉树
3.二叉树的遍历
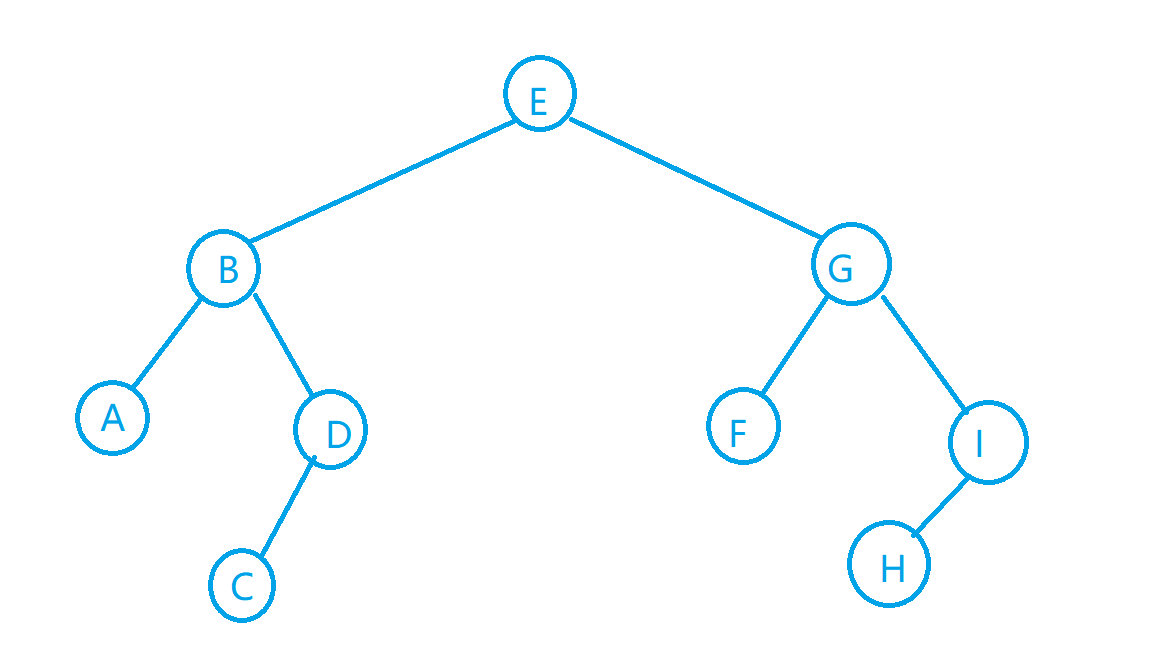
1.BFS 按层遍历
如图,按E−BG−ADFI−CH顺序搜索。
2.DFS
(1)先序遍历。父-左-右
如图,按EBADCGFIH顺序遍历。
(2)中序遍历。左-父-右
如图,按ABCDEFGHI顺序遍历。
二叉搜索树中排序是中序遍历,特征:
若已知根节点,则根节点左边的数都在左子树上,右边的数都在右子树上,对其子树也是如此。
(3)后序遍历。左-右-父
如图,按ACDBFHIGE顺序遍历。

