历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

浅谈 FFT (1)

作者：

垫底抽风 , 2020-08-06 13:35:25 , 所有人可见 , 阅读 4035

70

82

我本来是想一次把 FFT 各种优化和 NTT 都写完的，结果刚写完递归实现的 FFT，就已经 $1000$ 多行了

再加上可能用的 $\LaTeX$ 比较多，导致在编辑的时候巨卡无比，所以将整个分享拆成几部分来写

这篇是第一部分 ~~至于第二部分与后面的我可能会咕咕咕很久~~

$\text{update:}$ 浅谈 FFT (2){:target=”_blank”}

一、从系数表示法到点值表示法

先写一下暴力的解法

#include <cstdio>

const int N = 1005;

int n, m;
int a[N], b[N], c[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i <= n; i ++ )
        scanf("%d", a + i);
    for (int i = 0; i <= m; i ++ )
        scanf("%d", b + i);

    for (int i = 0; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ )
            c[i + j] += a[i] * b[j];

    for (int i = 0; i <= n + m; i ++ )
        printf("%d ", c[i]);

    return 0;
}

这个做法是通过定义直接求 $A$ 和 $B$ 的乘积的，

让多项式 $A$ 的每一项系数乘上 $B$ 的每一项系数，

总的时间复杂度为 $O(nm)$。

在这种做法上，我们很难再对其进行优化，

既然这样，我们就直接换一种表示多项式的方式，

这就是快速多项式乘法和暴力乘的本质区别。

$$ $$

1.1 系数表示法

一个 $n - 1$ 次多项式 $A(x)$ 可以表示为如下形式
$A(x) = a _ 0 + a _ 1 x + \cdots + a _ {n - 1} x ^ {n - 1} = \sum _ {i = 0} ^ {n - 1} a _ i x ^ i$

例如当 $n = 3, a = \{5, 2, 1\}$ 时，
$A(x) = 5 + 2x + x ^ 2$

那么对于 $n - 1$ 次多项式 $A(x)$ 和 $m - 1$ 次多项式 $B(x)$
$ A(x) = a _ 0 + a _ 1 x + \cdots + a _ {n - 1} x ^ {n - 1} \\\ B(x) = b _ 0 + b _ 1 x + \cdots + b _ {m - 1} x ^ {m - 1} $

有
$ A(x) B(x) = \sum _ {i = 0} ^ {n - 1} \sum _ {j = 0} ^ {m - 1} a _ i b _ j x ^ {i + j} = \\\ a _ 0 b _ 0 + a _ 0 b _ 1 x + \cdots + a _ 0 b _ {m - 1} x ^ {m - 1} \\\ a _ 1 b _ 0 x + a _ 1 b _ 1 x ^ 2 + \cdots + a _ 1 b _ {m - 1} x ^ m \\\ \qquad \qquad \qquad \qquad \vdots \\\ a _ {n - 1} b _ 0 x ^ {n - 1} + a _ {n - 1} b _ 1 x ^ n + \cdots + a _ {n - 1} b _ {m - 1} x ^ {n + m - 2} \\\ $

通过这种表示方式来计算多项式乘积，时间复杂度为 $O(nm)$

$$ $$

1.2 点值表示法

将 $n$ 组互不相同的 $x$ 代入多项式 $A$，得到 $n$ 个对应的 $y$ 值

注意，这里有可能得到两个相同的 $y$ 值，网上有很多有关 $FFT$ 的博客里写的是 得到n个不同的y

则该多项式被这 $n$ 组 $(x, y)$ 唯一确定，先感性的理解下，这里不严谨证明了。

把 $n$ 组 $(x, y)$ 代入一个 $n - 1$ 多项式，可以得到一个 $n$ 元一次方程组，

由于 $n$ 组 $(x, y)$ 互不相同（$y$ 有可能相同，但 $x$ 互不相同），所以这个 $n$ 元一次方程组有唯一解，

解出的 $n$ 个值即为原函数中 $n$ 个系数，原函数便被唯一确定了。

那么对于 $n - 1$ 次多项式 $A(x)$，可以被表示为如下形式

$ A(x) = \{(x _ 0, y _ 0), (x _ 1, y _ 1), \cdots, (x _ {n - 1}, y _ {n - 1})\} \\\ \qquad = \{(x _ 0, A(x _ 0)), (x _ 1, A(x _ 1)), \cdots (x _ {n - 1}, A(x _ {n - 1})\} \\\ $

这么光列式子有点抽象哈，举个栗子

对于 $2$ 次多项式 $A(x) = 5 + 2x + x ^ 2$

令 $x = -2, -1, 0$ 分别代入，得到对应的 $y = 5, 4, 5$

那么 $A(x)$ 就可以表示成如下形式

$A(x) = \{(-2, 5), (-1, 4), (0, 5)\}$

$$ $$

1.3 点值表示法的优势

那么这么做有什么好处呢？
将两个点值表示的多项式相乘，可以在 $O(n + m)$ 的时间复杂度之内完成！

观察点值表示的 $n - 1$ 次多项式 $A(x)$、$m - 1$ 次多项式 $B(x)$ 和它们的乘积 $A(x) B(x)$

（这里是将 $n + m$ 组 $x$ 代入两个多项式求点值表示）

$ A(x) = \{(x _ 0, A(x _ 0)), (x _ 1, A(x _ 1)), \cdots, (x _ {n + m - 1}, A(x _ {n + m - 1}))\} \\\ B(x) = \{(x _ 0, B(x _ 0)), (x _ 1, B(x _ 1)), \cdots, (x _ {n + m - 1}, B(x _ {n + m - 1}))\} \\\ A(x) B(x) = \{(x _ 0, A(x _ 0) B(x _ 0)), (x _ 1, A(x _ 1) B(x _ 1)), \cdots, (x _ {n + m - 1}, A(x _ {n + m - 1}) B(x _ {n + m - 1}))\} \\\ $

我们发现，计算出所有的 $A(x _ i)$ 之后，直接和 $B(x _ i)$ 相乘，即可得到 $A(x) B(x)$ 的点值表示的第 $i$ 项！

$$ $$

1.4 点值表示法的劣势

是不是突然感觉自己可以 $O(n)$ 虐爆所有高精度乘法题？

别忘了这是点值表示的情况，我们还要算上把系数表示的多项式转成点值表示的时间！

我们可以直接将 $n$ 个 $x$ 值带入，这样的确是能求出这个多项式的点值表示，

但是这么做每次求值要用 $O(n)$ 的时间求值，总的时间复杂度就还是 $O(n^2)$ 的呀！

$$ $$

二、一些前置知识

你应该已经意识到了，现在我们进行多项式乘法，时间复杂度瓶颈在于将系数表示法与点值表示法互相转换

而FFT/NTT，就是快速地将这两种表示法下的多项式互相转换

当然这么牛逼的东西可不是让你随随便便就能学会的，需要一些前置知识

哎先别走QAQ，我保证，如果你全神贯注地看，看一遍就能看懂

相信自己一定可以明白的，不要觉得它很难，不要因为文字太多而放弃

$$ $$

2.1 向量{:target=”_blank”}

2.1.1 向量定义与特点

向量，指具有大小和方向的量

它可以形象化地表示为带箭头的线段。

箭头所指：代表向量的方向；
线段长度：代表向量的大小。

2.1.2 向量的表示

在空间直角坐标系中，通常把向量以数对形式表示

例如 $xOy$ 平面中，如下箭头可以用数对 $(2, 3)$ 表示

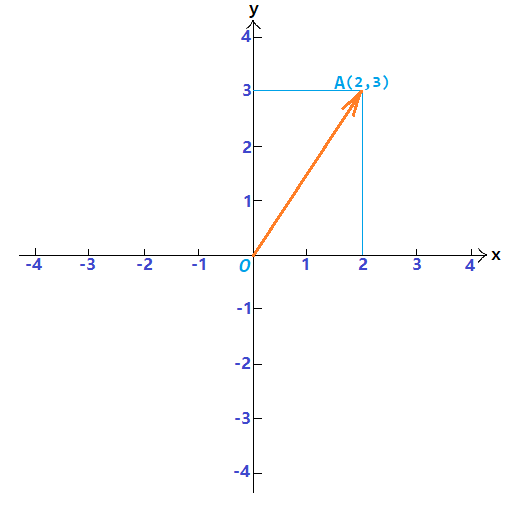
30334_18d02e38d6-无标题.png

也可以用 $\vec{OA}$ 表示

在二维中，每个向量可以用数对 $(x, y)$ 表示

三维中，向量可以用数对 $(x, y, z)$ 表示

在 $n$ 维中，向量可以表示为 $\vec{a} = (a _ 1, a _ 2, \ldots, a _ n)$

$$ $$

2.2 复数{:target=”_blank”}

2.2.1 复数定义

设 $a, b$ 为实数，$i ^ 2 = -1$，形如 $z = a + bi$ 的数叫复数

其中 $a$ 称为实部，$b$ 称为虚部，$i$ 称为虚数单位

当 $z$ 的虚部等于零时，常称 $z$ 为实数；

当 $z$ 的虚部不等于零，且实部等于零时，常称 $z$ 为纯虚数。

复数域是实数域的代数闭包{:target=”_blank”}，即任何复系数多项式在复数域中总有根。

2.2.2 复平面

复平面是一个平面，其中的每个点都表示一个复数

复数 $z = a + bi$ 在复平面中对应的坐标为 $(a, b)$

例如 $z = 2 + 3i$ 是一复数，在复平面中的坐标为 $(2, 3)$

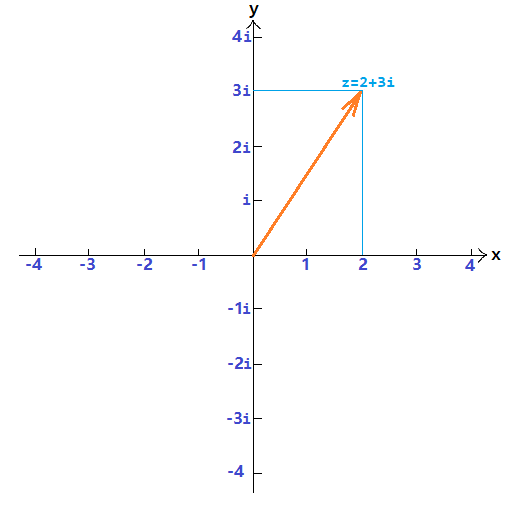
无标题.png

在复平面中

表示实数的点都在 $x$ 轴上，所以 $x$ 轴又称为实轴

表示纯虚数的点都在 $y$ 轴上，所以 $y$ 轴又称为虚轴

$y$ 轴上有且仅有一个实点即为原点 $(0, 0)$。

复平面内的每一个点，有唯一的一个复数和它对应

反过来，每一个复数，有复平面内有唯一的一个点和它对应

所以复数集 $C$ 和复平面内所有点所构成的集合是一一对应的。

2.2.3 复数的模

复数的实部与虚部的平方和的算术平方根称为该复数的模，记作 $|z|$

即对于复数 $z = a + bi$，它的模 $|z| = \sqrt {a ^ 2 + b ^ 2}$

这个符号和绝对值符号很像哈，其实可以直观的将其理解为复数的绝对值

绝对值的定义是实数轴上某个点到原点的距离

那么扩展到复平面上，也就是复数所对应的点到原点 $(0, 0)$ 的距离

复数 $z = a + bi$ 在复平面中的坐标为 $(a, b)$，到原点的距离正好是 $\sqrt{a ^ 2 + b ^ 2}$

所以 $|z| = \sqrt {a ^ 2 + b ^ 2}$ 也就不难理解啦~

2.2.4 复数的幅角

（这里用的是弧度制）

这个知识点不是很容易懂哈，看不懂也没关系，可以先跳过~

任意一个复数 $z$，都可以写成 $z = r \times (\cos \theta + i \sin \theta)$ 的形式

其中 $r$ 为 $z$ 的模，即 $r = |z|$，$\theta$ 为 $z$ 的幅角，记做 $Arg(z)$

任意一个不为 $0$ 的复数的幅角有无限多个取值，且这些值相差 $2 \pi$ 的整数倍。

我们把满足 $-\pi \leq \theta < \pi$ 的辐角 $θ$ 的值，叫做辐角的主值，记作 $arg(z)$（首字母小写），辐角的主值是唯一的。

比较抽象哈，举个例子

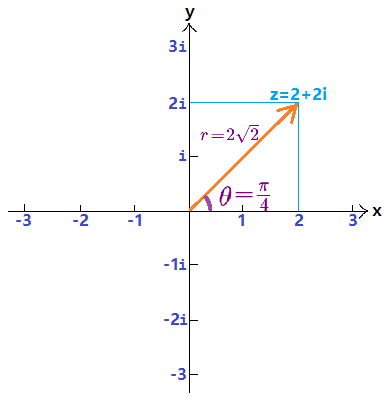
无标题.png

上图中 $z = 2 + 2i$，有 $r = |z| = \sqrt {2 ^ 2 + 2 ^ 2} = 2 \sqrt 2$

我们可以将 $z$ 写成 $z = 2 \sqrt 2 \times (\cos \frac \pi 4 + i \sin \frac \pi 4)$ 的形式

所以 $\frac \pi 4$ 是 $Arg(2 + 2i)$ 的一个取值

我们还可以将其写成 $z = 2 \sqrt 2 \times (\cos \frac {9 \pi} 4 + i \sin \frac {9 \pi} 4)$

所以 $\frac {9 \pi} 4$ 也是 $Arg(2 + 2i)$ 的一个取值

其中，该复数幅角的主值 $arg(2 + 2i) = \frac \pi 4$

直观的看，复数的幅角即为从 $x$ 轴正半轴到复数的转角

2.2.5 复数的运算法则

加法法则：

设复数 $z _ 1 = a _ 1 + b _ 1 i, z _ 2 = a _ 2 + b _ 2 i$

则
$\begin{aligned} z _ 1 + z _ 2 = &\ a _ 1 + b _ 1 i + a _ 2 + b _ 2 i \\\ = &\ (a _ 1 + a _ 2) + (b _ 1 + b _ 2) i \\\ \end{aligned} $

复数的加法和向量的加法都满足平行四边形定则{:target=”blank”}

乘法法则

几何定义：

（这个需要一点三角函数的知识哈，看不太懂可以先记下来）

复数相乘，模长相乘，幅角相加

即若复数 $z _ 1 = r _ 1 (\cos \theta _ 1 + i \sin \theta _ 1), z _ 2 = r _ 2 (\cos \theta _ 2 + i \sin \theta _ 2)$

其中 $r _ 1$ 和 $r _ 2$ 分别为 $z _ 1$、$z _ 2$ 的模

则 $z _ 1 z _ 2 = r _ 1 r _ 2 (\cos(\theta _ 1 + \theta _ 2) + i \sin (\theta _ 1 + \theta _ 2))$

代数定义

设复数 $z _ 1 = a _ 1 + b _ 1 i, z _ 2 = a _ 2 + b _ 2 i$

则
$\begin{aligned} z _ 1 z _ 2 = &\ (a _ 1 + b _ 1 i) (a _ 2 + b _ 2 i) \\\ \\\ = &\ a _ 1 a _ 2 + a _ 1 b _ 2 i + a _ 2 b _ 1 i - b _ 1 b _ 2 \\\ \\\ = &\ (a _ 1 a _ 2 - b _ 1 b _ 2) + (a _ 1 b _ 2 + a _ 2 b _ 1) i \end{aligned} $

2.3 单位根{:target=”_blank”}（这个很重要！！）

从这里开始，默认 $n$ 为 $2$ 的正整数次幂

2.3.1 单位根的定义

在复平面中，以原点 $(0, 0)$ 为圆心，$1$ 为半径作圆，将所作的圆称为单位圆

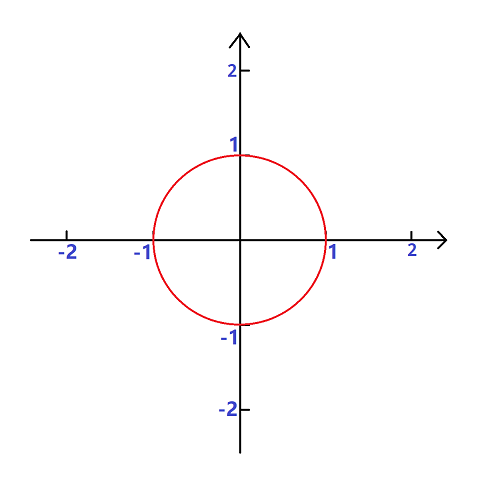
30334_18d02e38d6-无标题.png

我们将圆 $n$ 等分，并将每个等分点标号

（这里仅给出 $n = 4$ 和 $n = 8$ 时的情况。图中蓝色数字为坐标，绿色数字为每个点的编号。）

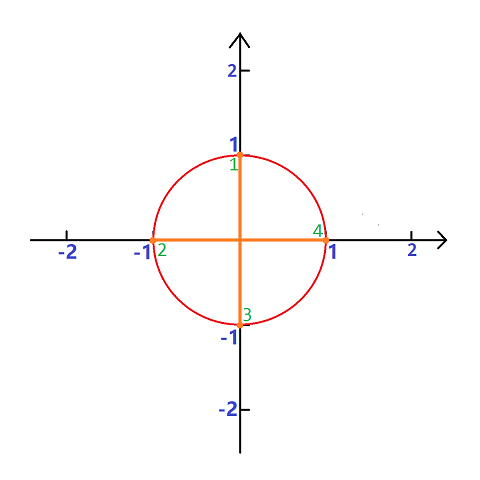
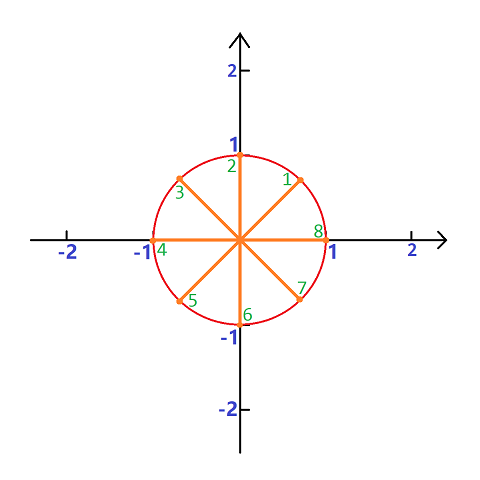
30334_18d02e38d6-无标题.png

我们将 $n$ 等分后的 $1$ 号点记做 $\omega _ n$，称为 $n$ 次单位根

2.3.2 单位根的性质

性质 $1: $

设 $n$ 等分后的 $j$ 号点的值为 $z _ j$，则有 $z _ j = z _ 1 ^ j = \omega _ n ^ j$

（这里为什么用 $j$ 呢？因为 $i$ 已经被用过了。。。）

证明：

根据上图，等分后，$j$ 号点模长为 $1$，幅角为 $\frac {2 j \pi} n$

那就可以将其表示为 $z _ j = \cos \frac {2 j \pi} n + i \sin \frac {2 j \pi} n$

根据模长相乘，幅角相加，可得

$ \begin{aligned} z _ 1 z _ j = &\ \cos \frac {2 \pi + 2 j \pi} n + i \sin \frac {2 \pi + 2 j \pi} n \\\ = &\ \cos \frac {2 (j + 1) \pi} n + i \sin \frac {2 (j + 1) \pi} n \\\ = & z _ {j + 1} \\\ \end{aligned} $

故 $z _ j = z _ 1 ^ j$

（这里看不懂的话，感性理解下就好啦~）

根据这个性质，等分后的 $n$ 个点都可以被 $1$ 号点表示出来

性质 $2 :\omega _ {2 n} ^ {2 j} = \omega _ n ^ j$

证明：

~~emm这个看图就能看出来~~
$ \begin{aligned} \omega _ {2 n} ^ {2 j} = &\ \cos \frac {4 j \pi} {2 n} + i \sin \frac {4 j \pi} {2 n} \\\ = &\ \frac {2 j \pi} n + i \sin \frac {2 j \pi} n \\\ = &\ \omega _ n ^ j \end{aligned} $

性质 $3 :\omega _ {2 n} ^ n = -1$

证明：
$ \begin{aligned} \omega _ {2 n} ^ n = &\ \cos \frac {2 n \pi} {2 n} + i \sin \frac {2 j \pi} {2 n} \\\ = &\ \cos \pi + i \sin \pi \\\ = &\ -1 + i \times 0 \\\ = &\ -1 \end{aligned} $

性质 $4 :\omega _ {2 n} ^ {k + n} = - \omega _ {2 n} ^ k$

证明：
$ \begin{aligned} \omega _ {2 n} ^ {k + n} = &\ \omega _ {2 n} ^ k \times \omega _ {2 n} ^ n \\\ = &\ \omega _ {2 n} ^ k \times -1 \\\ = &\ - \omega _ {2 n} ^ k \\\ \end{aligned} $

性质 $5 :\omega _ n ^ {k + n} = \omega _ n ^ k$

证明：
$ \begin{aligned} \omega _ n ^ {k + n} = &\ \omega _ n ^ {k + \frac n 2} \times \omega _ n ^ \frac n 2 \\\ = &\ -\omega _ n ^ k \times -1 \\\ = &\ \omega _ n ^ k \\\ \end{aligned} $

根据性质 $5$，可得 $\omega _ n ^ 0 = \omega _ n ^ n$

$$ $$

三、傅里叶变换

接下来，进入正题

3.1 FFT 快速傅里叶变换

3.1.1 理论知识

回归最开始讨论的内容，多项式

同上，默认 $n$ 为 $2$ 的正整数次幂，不足则在多项式后面补 $0$

设一个 $n$ 次多项式 $A(x) = a _ 0 + a _ 1 x + a _ 2 x ^ 2 \cdots + a _ {n - 2} x ^ {n - 2} + a _ {n - 1} x ^ {n - 1}$

将其每项按所在位置的奇偶性分成两部分，得

$A(x) = (a _ 0 + a _ 2 x ^ 2 + \cdots + a _ {n - 2} x ^ {n - 2}) + (a _ 1 x + a _ 3 x ^ 3 + \cdots + a _ {n - 1} x ^ {n - 1}) $

设

$A _ 1(x) = a _ 0 + a _ 2 x + \cdots + a _ {n - 2} x ^ {\frac n 2 - 1}$

$A _ 2(x) = a _ 1 + a _ 3 x + \cdots + a _ {n - 1} x ^ {\frac n 2 - 1}$

那么有

$ \begin{aligned} A (x) = A _ 1(x ^ 2) + x A _ 2(x ^ 2) \\\ \end{aligned} $

假设 $0 \leq k < \frac n 2$，将 $x = \omega _ n ^ k$ 代入，得

$A(\omega _ n ^ k) = A _ 1(\omega _ n ^ {2 k}) + \omega _ n ^ k A _ 2(\omega _ n ^ {2 k})$

将 $x = \omega _ n ^ {k + \frac n 2}$ 代入，得

$ \begin{aligned} A(\omega _ n ^ {k + \frac n 2}) = &\ A _ 1(\omega _ n ^ {2 k + n}) + \omega _ n ^ {k + \frac n 2} A _ 2(\omega _ n ^ {2 k + n}) \\\ \\\ = &\ A _ 1(\omega _ n ^ {2 k}) + \omega _ n ^ {k + \frac n 2} A _ 2(\omega _ n ^ {2 k}) \quad (根据性质 5) \\\ \\\ = &\ A _ 1(\omega _ n ^ {2 k}) - \omega _ n ^ k A _ 2(\omega _ n ^ {2 k}) \quad (根据性质 4) \\\ \\\ \end{aligned} $

发现了吗？
没发现的话，对比一下再看看？

$ \begin{aligned} A(\omega _ n ^ k) = &\ A _ 1(\omega _ n ^ {2 k}) + \omega _ n ^ k A _ 2(\omega _ n ^ {2 k}) \\\ A(\omega _ n ^ {k + \frac n 2}) = &\ A _ 1(\omega _ n ^ {2 k}) - \omega _ n ^ {k} A _ 2(\omega _ n ^ {2 k}) \\\ \end{aligned} $

没错！这两个式子只有一个符号不同！

那也就是说，我们在求 $A(\omega _ n ^ k)$ 的时候，可以 $O(1)$ 得到第二个式子的值！

而第一个式子，在 $k$ 取遍 $[0 \sim \frac n 2 - 1]$ 时，第二个式子正好取遍 $[\frac n 2 \sim n - 1]$！

那么我们就只需要将 $[0 \sim \frac n 2 - 1]$ 的所有值代入 $A$ 求值即可，

原问题缩小了一半！！

不仅如此，子问题还是满足原问题的性质的，所以我们就可以递归分治去做！！

递归边界：整个式子只剩一项，直接返回即可

3.1.2 时间复杂度分析

在每层递归中，将原函数的奇数项和偶数项分别处理，

所以最多只会递归 $\log n$ 层

每层递归中

要将原函数的奇数项和偶数项分离开，时间复杂度为 $O(n)$
用得到的值，求出 $A(\omega _ n ^ k)$ 和 $A(\omega _ n ^ {k + \frac n 2})$ 的值 $(0 \leq k < \frac n 2)$，时间复杂度 $O(n)$

所以总的时间复杂度为 $\log n \times O(n) = O(n \log n)$

3.1.3 C ++ 代码实现

代码中要用到虚数，可以直接使用 STL 的 complex

但不开 O2 可能会被卡

这里先给出手写 complex 的板子

由于在 $FFT$ 中暂时不需要除法，所以就先不写除法了

typedef struct complex
{
    // a 为实部，b 为虚部
    double a, b;

    complex(double x = 0, double y = 0)
    {
        a = x, b = y;
    }

    // 重载加法
    complex operator + (const complex &t) const
    {
        return complex(a + t.a, b + t.b);
    }

    // 重载减法
    complex operator - (const complex &t) const
    {
        return complex(a - t.a, b - t.b);
    }

    // 重载乘法，上面 2.2.5 的乘法法则中有推导过程
    complex operator * (const complex &t) const
    {
        return complex(a * t.a - b * t.b, a * t.b + b * t.a);
    }
} cp;

下面是用递归FFT将系数表示法转换成点值表示法的代码

这段代码跑完后，a[i] 存的是 $A(\omega _ n ^ i)$ 的值

// 将 n 次多项式 a 从系数表示转为点值表示
void FFT(cp a[], int n)
{
    // 如果 a 中只剩一项，直接返回
    if (n == 1) return;
    cp t[N];        // 临时数组

    int m = n >> 1; // 分成相等长度的两个多项式处理
    for (int i = 0; i < m; i ++ )
        t[i] = a[i << 1],         // t[0 ~ m) 存偶数项
        t[i + m] = a[i << 1 | 1]; // t[m ~ n) 存奇数项

    FFT(t, m);     // 分治处理偶数项
    FFT(t + m, m); // 分治处理奇数项
    // 这两个递归做完后，
    // t[0 ~ m) 中，t[i] 存的是 A_1(omega_n ^ 2i) 的值 (0 <= k < m = n / 2)
    // t[m ~ n) 中，t[i] 存的是 A_2(omega_n ^ 2i) 的值 (0 <= k < m = n / 2)

    // 合并到 a 中
    for (int i = 0, j = m; i < m; i ++ , j ++ )
    {
        // 计算 omega_n ^ i 的值，存入 x 中
        cp x(cos(2 * pi * i / n), sin(2 * pi * i / n));
        // 根据上面两个式子，分别求出 k 取 1 ~ n/2 时，
        // A(omega_n ^ k) 和 A(omega_n ^ (k + n/2)) 的值
        a[i] = t[i] + x * t[j];
        a[j] = t[i] - x * t[j];
    }
}

3.2 IFFT 快速傅里叶逆变换

别忘了，我们现在只解决了将系数表示法转换成点值表示法的问题

我们将两个多项式转换到点痣表示法后，再做乘积，得到的是点值表示法下的乘积

但我们平时用系数表示的多项式，对我们而言，点值表示的多项式没有意义

现在我们要考虑如何快速地将点值表示法转换成系数表示法，这个过程叫做傅里叶逆变换

这里先给出结论，再给出推导过程。因为这个结论的确很难想出来

3.2.1 理论知识

结论：

设函数

$ \begin{aligned} A(x) = a _ 0 + a _ 1 x + a _ 2 x ^ 2 + \cdots + a _ {n - 2} x ^ {n - 2} + a _ {n - 1} x ^ {n - 1} \end{aligned} $

那么有

$ a _ i = \displaystyle \frac { \begin{aligned} \sum _ {j = 0} ^ {n - 1} A(\omega _ n ^ j) \omega _ n ^ {- i j} \end{aligned} } n $

证明：

这个证明比较高能，请做好心理准备

推式子，先将分子那项提出来

$ \begin{aligned} & \sum _ {j = 0} ^ {n - 1} A(\omega _ n ^ j) \omega _ n ^ {- i j} \\\ \\\ & = \sum _ {j = 0} ^ {n - 1} \omega _ n ^ {- i j} \sum _ {k = 0} ^ {n - 1} a _ k (\omega _ n ^ j) ^ k \qquad (将 A(\omega _ n ^ j) 拆开) \\\ \\\ & = \sum _ {j = 0} ^ {n - 1} \sum _ {k = 0} ^ {n - 1} a _ k \omega _ n ^ {j k} \omega _ n ^ {- i j} \qquad (将 \omega _ n ^ {- i j} 乘到里面去，(\omega _ n ^ j) ^ k 指数展开) \\\ \\\ & = \sum _ {j = 0} ^ {n - 1} \sum _ {k = 0} ^ {n - 1} a _ k (\omega _ n ^ {k - i}) ^ j \qquad (将 \omega _ n ^ {j k} \omega _ n ^ {- i j} 合并) \\\ \\\ & = \sum _ {k = 0} ^ {n - 1} a _ k \sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j \qquad (交换求和顺序) \\\ \end{aligned} $

观察 $ \begin{aligned} \sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j \\\ \end{aligned} $ 这项，

设 $\begin{aligned} S = \sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j = 1 + \omega _ n ^ {k - i} + (\omega _ n ^ {k - i}) ^ 2 + \cdots + (\omega _ n ^ {k - i}) ^ {n - 2} + (\omega _ n ^ {k - i}) ^ {n - 1} \\\ \end{aligned} $

那么有 $\begin{aligned} \omega _ n ^ {k - i} S = &\ \omega _ n ^ {k - i} + (\omega _ n ^ {k - i}) ^ 2 + (\omega _ n ^ {k - i}) ^ 3 \cdots + \cdots (\omega _ n ^ {k - i}) ^ {n - 1} + (\omega _ n ^ {k - i}) ^ n \\\ = &\ S - 1 + (\omega _ n ^ {k - i}) ^ n \\\ \end{aligned}$

得 $\omega _ n ^ {k - i} S = S + (\omega _ n ^ {k - i}) ^ n - 1$

$(\omega _ n ^ {k - i} - 1) S = (\omega _ n ^ {k - i}) ^ n - 1$

当 $\omega _ n ^ {k - i} = 1$ 时，即 $k \equiv i \ (\text{mod}\ n)$ 时，

$S = 1 + 1 + 1 + \cdots + 1 = n$

当 $\omega _ n ^ {k - i} \neq 1$ 时，即 $k \not \equiv i \ (\text{mod}\ n)$ 时，可以将两边同时 $\div (\omega _ n ^ {k - i} - 1)$，得

$ \begin{aligned} S = &\ \frac {(\omega _ n ^ {k - i}) ^ n - 1} {\omega _ n ^ {k - i} - 1} \\\ \\\ = &\ \frac {(\omega _ n ^ n) ^ {k - i} - 1} {\omega _ n ^ {k - i} - 1} \\\ \\\ = &\ \frac {1 ^ {k - i} - 1} {\omega _ n ^ {k - i} - 1} \\\ \end{aligned} $

注意到此时分子为零，且分母不为零，故 $S = 0$

所以有 $\begin{aligned} \sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j = \left\{ \begin{aligned} & n & \text{if}\ k \equiv i\ (\text{mod}\ n) \\\ & 0 & \text{if}\ k \not \equiv i\ (\text{mod}\ n) \\\ \end{aligned} \right. \end{aligned} $

那么在 $\begin{aligned} \sum _ {k = 0} ^ {n - 1} a _ k (\sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j) \end{aligned}$ 中，对于后面求和那项的值

当 $k = i$ 时，值为 $n$

当 $k \neq i$ 时，值为 $0$
所以原式 $ \begin{aligned} \\\ \displaystyle \frac { \begin{aligned} \sum _ {j = 0} ^ {n - 1} A(\omega _ n ^ j) \omega _ n ^ {- i j} \end{aligned} } n = &\ \frac { \begin{aligned} \sum _ {k = 0} ^ {n - 1} a _ k (\sum _ {j = 0} ^ {n - 1} (\omega _ n ^ {k - i}) ^ j) \end{aligned} } n \\\ = &\ \frac {n \times a _ i} n \\\ = &\ a _ i \\\ \end{aligned} $

证毕

3.2.2 时间复杂度分析

由于我们是已经知道了所有 $A(\omega _ n ^ j)$ 的值的，

所以我们在求解 $\begin{aligned} \sum _ {j = 0} ^ {n - 1} A(\omega _ n ^ j) \omega _ n ^ {- i j} \end{aligned}$ 的时候呢，

那么我们就可以将这个式子中的 $A(\omega _ n ^ j)$ 看做是整个多项式的系数，

而将 $\omega _ n ^ {-i}$ 看做是整个多项式的自变量，

那么我们就可以通过快速傅里叶变换，做这个快速傅里叶逆变换

时间复杂度为 $O(n \log n)$

3.2.3 C ++ 代码实现

void FFT(cp a[], int n)
{
    if (n == 1) return;
    cp t[N];

    int m = n >> 1;
    for (int i = 0; i < m; i ++ )
        t[i] = a[i << 1],
        t[i + m] = a[i << 1 | 1];

    FFT(t, m);
    FFT(t + m, m);
    for (int i = 0, j = m; i < m; i ++ , j ++ )
    {
        // 这里只需要将后面的 sin(2 pi i / n) 改为 -sin(2 * pi * i / n) 即可
        // 这么改的原因，是因为我们在该函数中，代入的变量变成了 omega_n ^ -i
        // 而 omega_n ^ -i = cos(2 * pi * -i / n) + sin(2 * pi * -i / n)
        // = cos(2 * pi * i / n) - sin(2 * pi * i / n) （诱导公式三）
        cp x(cos(2 * pi * i / n), -sin(2 * pi * i / n));
        a[i] = t[i] + x * t[j];
        a[j] = t[i] - x * t[j];
    }
}

3.3 多项式乘法的递归实现

loj上的板子题{:target=”_blank”}

刚才我们已经学过 $\text{FFT}$ 和 $\text{IFFT}$ 了

由于两个 FFT 中，只有一个符号不同

所以可以只写一个 FFT 函数，并传一个额外参数

即可完成快速傅里叶变换与快速傅里叶逆变换

C ++ 代码

#include <cmath>
#include <cstdio>

// 手写 complex 的板子
// emmm话说我为什么手写还要 typedef
typedef struct complex
{
    double a, b;

    complex(double x = 0, double y = 0)
    {
        a = x, b = y;
    }

    complex operator + (const complex &t) const
    {
        return complex(a + t.a, b + t.b);
    }

    complex operator - (const complex &t) const
    {
        return complex(a - t.a, b - t.b);
    }

    complex operator * (const complex &t) const
    {
        return complex(a * t.a - b * t.b, a * t.b + b * t.a);
    }
} cp;
// 此题中两个多项式最多都是 1e5 次的
// 那么两个多项式的乘积最多就是 2e5 次的
// 由于如果两个多项式乘积的次数不为 2 的整次幂，要在前面补项
// 所以这里为了保险，开到 4e5
const int N = 400005;
const double pi = 2 * acos(-1); // 由于后面用到的都是 2pi，这里直接让 pi 存 2pi 的值

int n, m;      // 分别存两个多项式的次数
cp a[N], b[N]; // 存两个多项式

// 参数中多了一个 f，用于存类型
// 当 f 为 1 时，是将系数表示转点值表示
// 当 f 为 -1 时，是将点痣表示转系数表示
void FFT(cp a[], int n, int f)
{
    if (n == 1) return;
    cp t[N];

    int m = n >> 1;
    for (int i = 0; i < m; i ++ )
        t[i] = a[i << 1],
        t[i + m] = a[i << 1 | 1];

    FFT(t, m, f);
    FFT(t + m, m, f);

    for (int i = 0, j = m; i < m; i ++ , j ++ )
    {
        cp x(cos(pi * i / n), f * sin(pi * i / n));
        a[i] = t[i] + x * t[j];
        a[j] = t[i] - x * t[j];
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    // 将 A 的每项系数存入数组 a 中
    for (int i = 0; i <= n; i ++ )
    {
        double x;
        scanf("%lf", &x);
        a[i] = {x, 0};
    }
    // 将 B 的每项系数存入数组 b 中
    for (int i = 0; i <= m; i ++ )
    {
        double x;
        scanf("%lf", &x);
        b[i] = {x, 0};
    }

    // 由于我们要求多项式长度为 2 的整次幂
    // 如果乘积多项式不足 2 的整次幂，要补项
    // 这里用 k 存补后的多项式的次数
    int k = 1;
    while(k <= n + m) k *= 2;

    // 将 A 和 B 转成点值表示
    FFT(a, k, 1);
    FFT(b, k, 1);

    // 转成点值表示后 O(n + m) 做多项式乘法
    // 将结果储存到 a 中
    for (int i = 0; i < k; i ++ ) a[i] = a[i] * b[i];

    // 将乘积转成系数表示
    FFT(a, k, -1);

    // 输出转成系数表示后的多项式
    for (int i = 0; i <= n + m; i ++ )
        // 注意，我们最后所求得的，是上述分子中的那个和式
        // 我们要将其 / k 之后再输出
        // 由于浮点数运算有精度问题，这里需要四舍五入再输出
        printf("%d ", (int)(a[i].a / k + 0.5));

    return 0;
}

写完了，交上去一看

诶，怎么还 TLE 了。。

分析原因：

我们在每层递归中，要开一个成都为 $4 \times 10 ^ 5$ 的临时数组

每次开一个数组就要超过 $10ms$ 的时间，导致的 TLE

（话说栈空间的限制放开啦？？不应该 MLE 的嘛？？）

我们可以开一个静态数组

每次将 a 复制到静态数组后，再从静态数组复制回来，再对 a 做后面的操作

C ++ 代码

#include <cmath>
#include <cstdio>
#include <cstring>

typedef struct complex
{
    double a, b;

    complex(double x = 0, double y = 0)
    {
        a = x, b = y;
    }

    complex operator + (const complex &t) const
    {
        return complex(a + t.a, b + t.b);
    }

    complex operator - (const complex &t) const
    {
        return complex(a - t.a, b - t.b);
    }

    complex operator * (const complex &t) const
    {
        return complex(a * t.a - b * t.b, a * t.b + b * t.a);
    }
} cp;
const int N = 400005;
const double pi = 2 * acos(-1);

int n, m;
cp a[N], b[N];

void FFT(cp a[], int n, int f)
{
    if (n == 1) return;
    static cp t[N];

    int m = n >> 1;
    for (int i = 0; i < m; i ++ )
        t[i] = a[i << 1],
        t[i + m] = a[i << 1 | 1];

    // 将 t 复制到 a 中
    // 这里偷个懒，就直接用 memcpy 了
    // 一个 double 占 8 个字节
    // complex 有两个 double，占了 16 个字节
    // 所以这里要将 n 乘 16
    memcpy(a, t, n << 4);

    // 然后对 a 做剩下的 FFT
    FFT(a, m, f);
    FFT(a + m, m, f);

    for (int i = 0, j = m; i < m; i ++ , j ++ )
    {
        cp x(cos(pi * i / n), f * sin(pi * i / n));
        t[i] = a[i] + x * a[j]; // 这里要改成从 a 到 t 做
        t[j] = a[i] - x * a[j];
    }

    // 然后再将 t 复制回 a
    memcpy(a, t, n << 4);
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 0; i <= n; i ++ )
    {
        double x;
        scanf("%lf", &x);
        a[i] = {x, 0};
    }
    for (int i = 0; i <= m; i ++ )
    {
        double x;
        scanf("%lf", &x);
        b[i] = {x, 0};
    }

    int k = 1;
    while(k <= n + m) k *= 2;

    FFT(a, k, 1);
    FFT(b, k, 1);

    for (int i = 0; i < k; i ++ ) a[i] = a[i] * b[i];

    FFT(a, k, -1);

    for (int i = 0; i <= n + m; i ++ )
        printf("%d ", (int)(a[i].a / k + 0.5));

    return 0;
}

下一章：浅谈 FFT (2){:target=”_blank”}

$$ $$