引子
- 冒泡排序,选择排序,插入排序,快速排序,堆排序,归并排序,希尔排序,桶排序,基数排序新年帮您排忧解难。
有向图,无向图,有环图,无环图,完全图,稠密图,稀疏图,拓扑图祝您新年宏图大展。最长路,最短路,单源路径,所有节点对路径祝您新年路路通畅。二叉树,红黑树,van Emode Boas树,最小生成树祝您新年好运枝繁叶茂。- 最大流,网络流,标准输入流,标准输出流,文件输入流,文件输出流祝您新年顺顺流流。
- 线性动归,区间动归,坐标动归,背包动归,树形动归为您的新年规划精彩。
- 散列表,哈希表,
邻接表,双向链表,循环链表帮您在新年表达喜悦。 - O(1),O(log n),O(n),
O(nlog n),O(n^2),O(n^3),O(2^n),O(n!)祝您新年渐进步步高。
图
- 图论[Graph Theory]是数学的一个分支。
它以图为研究对象,研究顶点和边组成的图形的数学理论和方法。 - 如你所见,图由点(我们放大为圆圈)和线组成(或者带箭头的线段)。
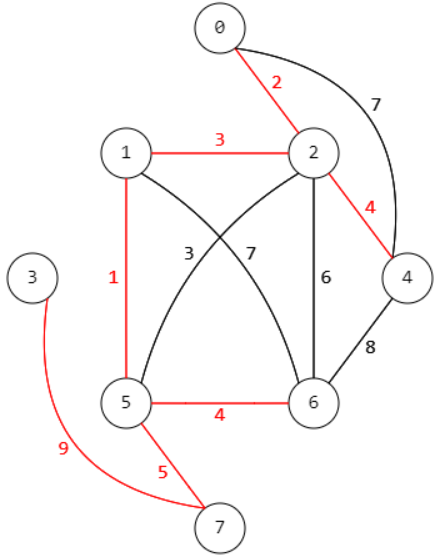
什么是图?
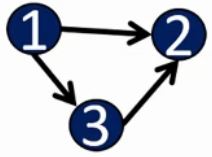
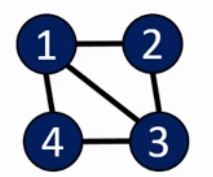
- 图由点和边组成。根据边是否有方向,可分为有向图、无向图。树是特殊的无向图。
有向图:
无向图:
- 每条边可以有一个长度,当然也可以没有(默认为1)。
- 图论题面中顶点的个数通常用$n$表示,边的数量通常用$m$表示,数据范围一般不对$n$,$m$进行解释。
- 一般图论题$n$,$m$数量级为$1e5$。
稀疏图与稠密图
- 边数 $e$ 和 $v(v-1)/2$ 相比非常少($e$、$v$同数量级)的称为稀疏图
- 时间复杂度为 $O(e\log e$ 的算法和 $O(v^2)$ 的算法对于稀疏图来说前者好,而对于稠密图来说后者好
欧拉路径与欧拉回路
- 遍历图 $G(V, E)$,只通过每条边一次的路径叫做欧拉路径;如果这条路径的起点和终点是同一点,称做欧拉回路。
- 对于无向图来说,图 $G$ 有一条欧拉路径,当且仅当 $G$ 是连通的,且有 $0$ 个或 $2$ 个 奇数度结点。当所有点是偶数度时欧拉回路起点可以是任意点;当有两个奇数度点时起点/终点必须是奇数度点。
- 对于有向图,存在欧拉路径的条件:图连通,所有点入度=出度,或者有 $1$ 个终点的入度-出度=$1$,有 $1$ 个起点的出度-入度=$1$。当所有点出度=入度时任意点可作为起点,而后者必须以出度-入度=$1$ 的点做起点,入度-出度=$1$ 的点做终点。
图的存储-邻接矩阵
- 我们选择用“邻接矩阵”表格的方式存储一个图。
- 存储规则:若$a$能直接到达$b$,则此表格第$a$行第$b$列的值就是$a$到$b$的直接距离(或$1$),无法访问为$-1$或正无穷。
- 特别的,自己到自己的距离为$0$。
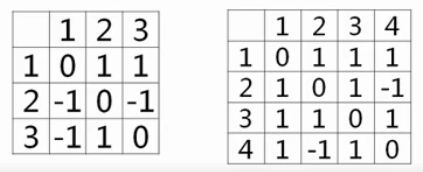
图的存储-邻接表
- 邻接表(链式前向星)存储图比邻接矩阵更加高效。
- 邻接表由点表(由点构成的表)(上)和边表(由边构成的表)(下)组成。
head数组存储的是以该点为起点(按照加入时间顺序)最后加入的一条边。- 边表
from数组实际操作没有用处,不过在查错环节还是有用的。 next数组是以该边为起点的上一条边(按照加入时间顺序)。
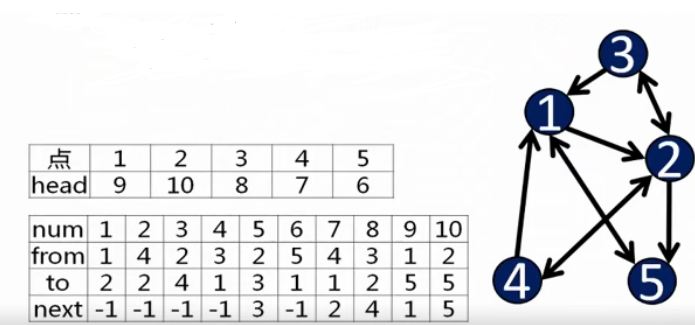
邻接表输入
读入边的列表($M$ 条边$\{u,v,w\}$),建立邻接表
struct Edge { // 建立邻接表
int v, w; // 边的终点v和边权w
Edge(int v, int w) : v(v), w(w) {} // 构造函数
};
vector<Edge> adj[N + 5]; // N为点数
for (int i = 1; i <= M; ++i) {
int u, v, w; // 边<u, v>的权为w
cin >> u >> v >> w;
adj[u].push_back(Edge(v, w));
adj[v].push_back(Edge(u, w)); // 若为无向图,建2条边
}
树
- 什么是树啊?
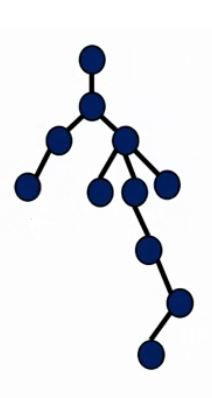
- 树是一个特殊的图罢了,没啥了不起的。
- 特殊在这个$n$节点的图里,有$n-1$条连接图的边,把这些点连接起来,恰好这些点可以联通。
- 连通无向无环图
- $G$ 有 $v - 1$ 条边,无环
- $G$ 有 $v - 1$ 条边,连通
- $G$ 连通,但任意删除一条边后不连通
- $G$ 无环,但任意添加一条边后包含环
- 任意两点只有唯一的简单路径
- 树的一些相关操作
(1) 树的重心和直径
(2) 倍增LCA
树的存储方式
- 父亲节点表示法
- 儿子节点表示法
- 无向图表示法
- 左儿子右兄弟-树转
二叉树
图的遍历
- 深度优先搜索
- 广度优先搜索
宽度优先遍历
- 从图上一个点开始,先访问距离它为 $1$ 的所有点,再访问距离它为 $2$ 的所有点
- 图上有可能有环,如果遇到一次访问回到一个遇到过的点,就不要再重复走了
- 可以用一个 $vis$ 数组标记走过的点
- 或者用 $dis$ 数组标记到达每个点的最短距离,当从 $u$ 到达 $v$ 的时候了,$dis[v] = dis[u] + 1$。当走之前发现 $dis[v]$ 已经比 $dis[u]$ 小,就不要走了。
例题1: 无权最短路
算法分析
- 定义一个 $dis$ 数组,用来表示从 $s$ 出发到每个点的最短路径的距离。初始都赋值为无穷大,然后把 $dis[s]$ 赋值为 $0$。
- 定义一个队列来做 $bfs$,初始把起点 $s$ 入队。
- 每次从队头拿出来一个点 $u$,在邻接矩阵里面,找当前点能到达的所有点 $v$,如果 $dis[v]$ 大于 $dis[u] + 1$,那么把 $dis[v]$ 改成 $dis[u] + 1$,然后 $v$ 点入队。因为是无权图,往前走一步,认为距离加一。
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::queue;
const int MAXN = 5005;
int adj[MAXN][MAXN];
int dis[MAXN];
int32_t main() {
int n, m, s, t;
cin >> n >> m >> s >> t;
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
adj[u][v] = adj[v][u] = 1;
}
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int u = q.front();
q.pop();
if (u == t) break;
for (int i = 1; i <= n; ++i) {
if (adj[u][i] && dis[i] > dis[u] + 1) {
dis[i] = dis[u] + 1;
q.push(i);
}
}
}
if (dis[t] == 0x3f3f3f3f) cout << "No path\n";
else cout << dis[t] << '\n';
return 0;
}
例题2:树的直径(简单版)
一颗树 $T$ 的“直径”定义为结点两两间距离的最大值。给定无权树 $T$,求 $T$ 的直径长度
输入格式
第一行包含 $1$ 个整数 $N$,表示图中共有 $N$个结点。 $(N \leqslant 5000)$
接下来 $N-1$ 行,每行包含 $3$ 个整数 $\{u, v, 1\}$,表示有一条无向边连接结点
* 输入保证是无环图
输出格式
一个整数,代表直径长度
算法分析
在树上随便找一个点 $u$,从 $u$ 出发,找到距离它最远的点 $v$。再从 $v$ 出发,找到距离它最远的点 $w$($w$有可能还是 $u$),则 $v$ 和 $w$ 之间的路径就是树的直径。
证明:1. 如果 $u$ 是直径的一个端点,那么因为 $v$ 是距离 $u$ 最远的点,$w$ 和 $u$ 也重合。这种情况下,$uv$ 就是直径。
2. 如果 $u$ 不是直径的端点,此时 $v$ 一定是端点。
因为假设 $v$ 也不是端点,此时直径的端点设为 $ab$,这时候有两种情况:
2.1 $a$ 不在 $uv$ 上,那么 $ua$ 比 $uv$ 更长,与前面假设 $v$ 到 $u$ 最远矛盾。
2.2 $a$ 在 $uv$ 上,这时候 $ub$ 比 $ab$ 长,与 $ab$ 是直径矛盾。
所以 $v$ 一定是直径端点,从 $v$ 出发到达的最远的点 $w$ ,则 $vw$ 是直径
所以求直径可以在树上做两遍最短路径。
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::memset;
using std::vector;
using std::queue;
int n;
vector<int> adj[5005];
int dis[5005];
int bfs(int u) {
int r = u;
memset(dis, 0x3f, sizeof(dis));
dis[u] = 0;
queue<int> q;
q.push(u);
while (!q.empty()) {
u = q.front();
q.pop();
for (int i = 0; i < adj[u].size(); ++i) {
int v = adj[u][i];
if (dis[v] > dis[u] + 1) {
dis[v] = dis[u] + 1;
q.push(v);
}
}
}
for (int i = 1; i <= n; ++i) {
if (dis[i] > dis[r]) {
r = i;
}
}
return r;
}
int main() {
cin >> n;
for (int i = 0; i < n - 1; ++i) {
int u, v, t;
cin >> u >> v >> t;
adj[u].push_back(v);
adj[v].push_back(u);
}
int r = bfs(1);
r = bfs(r);
cout << dis[r] << '\n';
return 0;
}
二分图判定
- 二分图,就是一张图的所有的点,可以分成两部分。所有的边都只有两部分中间相连,同一部分内部没有边。
- 如何判断一个图是二分图呢?可以用黑白染色的方法,任选一个没有颜色的点,染成 $1$,然后 $bfs$。每次从 $u$ 走到 $v$ 的时候,看看 $v$ 点的颜色,如果 $v$ 没有颜色,就染成和 $u$ 相反的颜色。如果 $v$ 点颜色和 $u$ 点颜色一致,就判断不是二分图。
- 重复以上过程,直到图中所有点都有颜色。或者已经判断出不是二分图。
例题:象棋比赛
一年一度的初中象棋比赛开始了,初一、初二年级都派出了很多选手(参赛选手共 $n$ 人),每一场对战只在来自两个不同年级的同学间进行,现在拿到了一张对阵表,不过表中只有每一场对战的选手的姓名,却没有标注他们的年级。
现在请你检查一下表中的对阵安排是否有错误,即是否把同一个年级的选手安排了对战。
输入格式
第 $1$ 行:$1$ 个正整数 $T(1 \leqslant T \leqslant 10)$
接下来 $T$ 组数据,每组数据按照以下格式给出:
第 $1$ 行:$2$ 个正整数 $n,m(1 \leqslant n \leqslant 10000, 1 \leqslant m \leqslant 40000)$
接下来 $m$ 行:每行三个整数 $u, v, w$,表示 $u$ 和 $v$ 之间有一条边,权重为 $w$ (恒为 $1$)
为方便处理,我们用 $1$ 至 $n$ 的编号表示不同的选手。
输出格式
$T$行:每行表示第 $i$ 组数据是否有误。如果是正确的数据输出 $”Correct”$,否则输出 $”Wrong”$
C++ 代码
bool bfs() {
// 初始化成0,然后每个位置用1和-1表示属于哪个阵营
memset(color, 0, sizeof(color));
for (int i = 1; i <= n; ++i) {
if (color[i] == 0) {
color[i] = 1;
queue<int> q;
q.push(i);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < adj[u].size(); ++i) {
int v = adj[u][i];
if (color[v] == 0) {
color[v] = -color[u];
q.push(v);
}
else if (color[v] == color[u]) {
// 发现一条边走到了一个跟自己一样的阵营,找到矛盾
return false;
}
}
}
}
}
return true;
}
深度优先遍历
- 只要可能,就在图中尽量“深入”
- 对最近才发现的节点 $v$ 的出发边进行搜索,直到该节点的所有出发边都被发现完为止
- 一旦节点 $v$ 的所有出发边都被发现,搜索则回溯到 $v$ 的前驱节点,来搜索前驱节点的出发边
- 该算法一直持续到从源节点到可以达到的所有节点都被发现为止
- 如果还存在尚未发现的节点,则从这些点中选取新的源点
简单路径数目
分析:从 $s$ 开始 $dfs$,走到一个点就在 $vis$ 数组里标记走过,避免走重复的点形成环。一旦走到 $t$,就统计个数加一。
C++ 代码:
// 本代码超时,可以用链式前向星存图来通过本题
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::vector;
using ll = long long;
const int N = 5010;
int n, m, s, t, vis[N];
ll cnt;
vector<int> adj[N]; // 邻接表
void dfs(int u) {
if (u == t) {
cnt++;
return;
}
for (int i = 0; i < adj[u].size(); ++i) {
int v = adj[u][i];
if (!vis[v]) {
vis[v] = 1;
dfs(v);
vis[v] = 0;
}
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
cin >> n >> m >> s >> t;
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
}
vis[s] = 1;
dfs(s);
if (cnt == 0) cout << "No Path!\n";
else cout << cnt << '\n';
return 0;
}
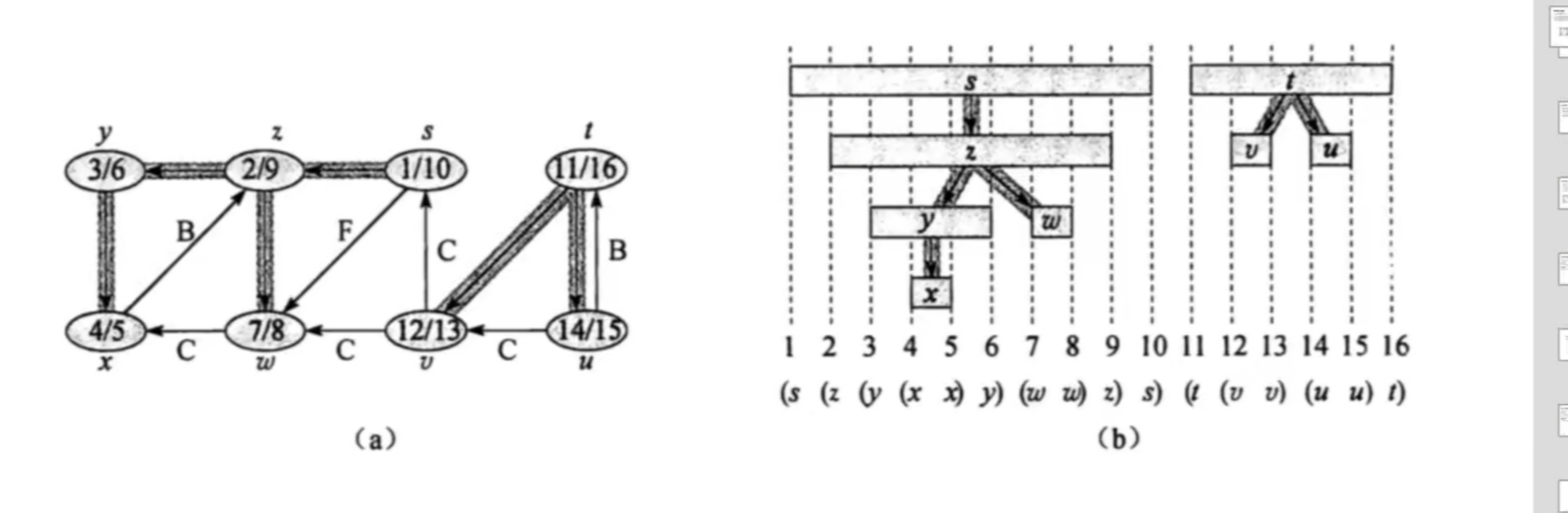
染色与时间戳
- 每个点初始颜色都是白色,在结点被发现后变成灰色,在其邻接链表扫描后变成黑色
- 引入时间戳概念,对于结点 $v$,变灰时间记录在 $pre[v]$ 中,变黑时间记录在 $post[v]$ 数组中
- 则对于每个结点有 $1 \leqslant pre[v] < post[v] \leqslant 2V$
- 对于 $pre$ 和 $post$ 数组,都初始化成 $0$,则可以用这两个数组来区分结点颜色
- 白色:$pre[v] = post[v] = 0$
- 灰色:$post[v] = 0$
- 黑色:$pre[v]$ 和 $post[v]$ 都不是 $0$
DFS 框架
void dfs(u) {
pre[u] = ++dfsTime;
for each (u, v) in E // 遍历u的所有出边
if (pre[v] == 0) { // 说明是白色的点,还没到过
dfs(v);
}
post[u] = ++dfsTime;
}
void dfsVisit() {
for each u int V
if (pre[u] == 0) {
dfs(u);
}
}
DFS 的性质
- 时间复杂度 $O(V + E)$
- 结点 $v$ 是深度优先森林里结点 $u$ 的后代,当且仅当结点 $v$ 在结点 $u$ 为灰色的时间段内被发现。
- 结点的发现时间和完成时间具有括号化结构,以 “(u” 来表示结点 $u$ 的发现,以 “u)” 来表示结点 $u$ 的完成,则所有结点访问的历史记载形成一个括号合法的表达式。



真不错