一、排序算法目录

---

1. 直接插入排序
2. 折半插入排序
3. 希尔排序
4. 冒泡排序
5. 快速排序
6. 选择排序
7. 归并排序
8. 堆排序
9. 计数排序
10. 桶排序

二、排序对比一览表

---

1. inference1
2. inference2

---

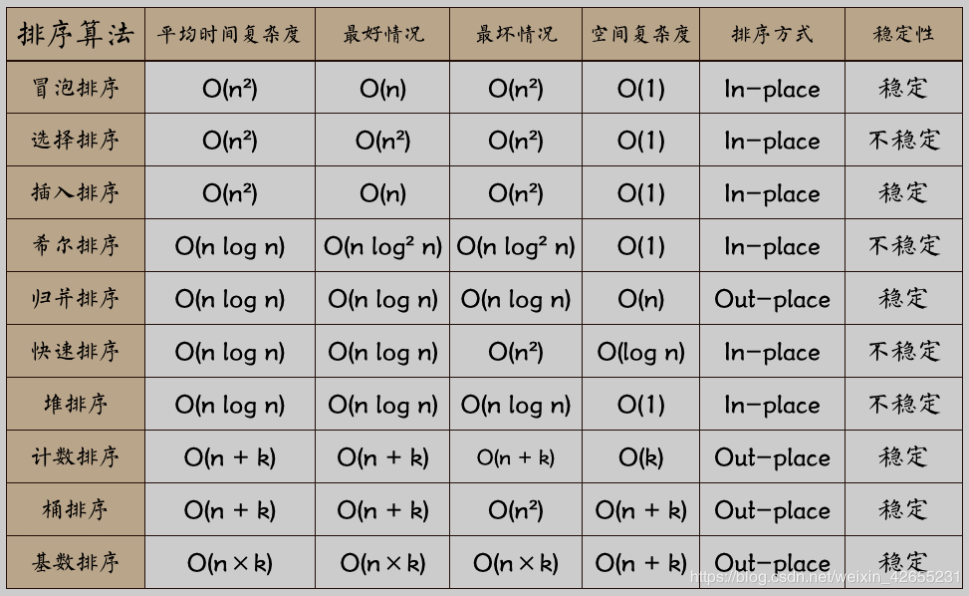
到文章末尾

---

三、插入类排序

1. 直接插入排序

算法思想

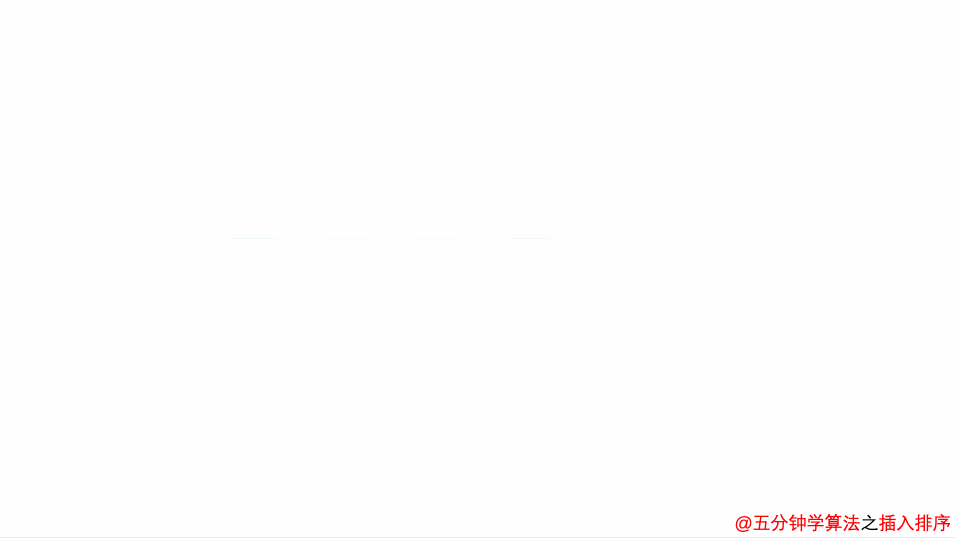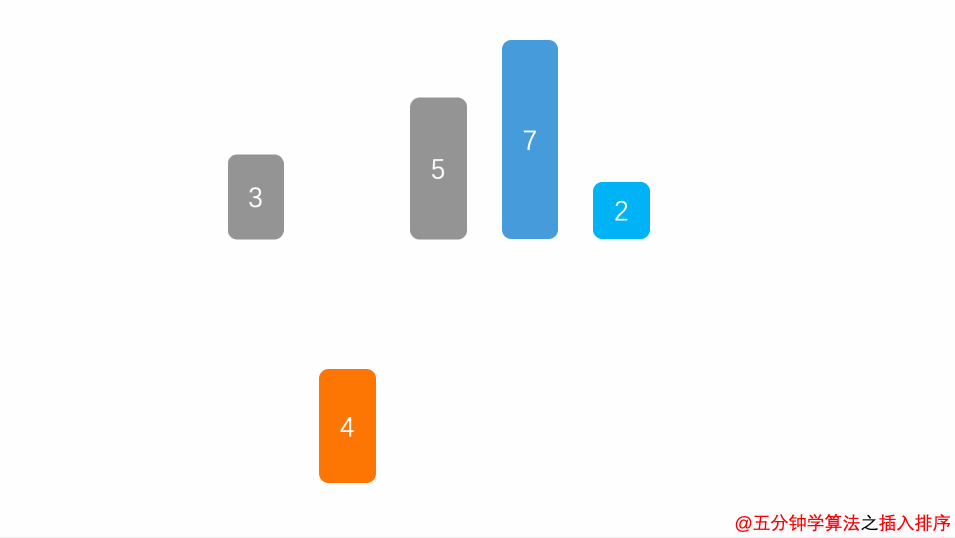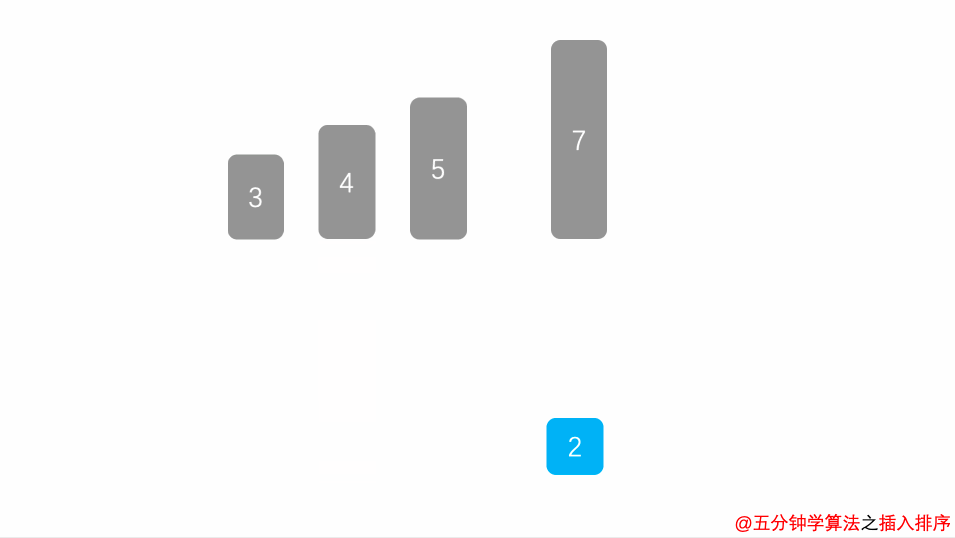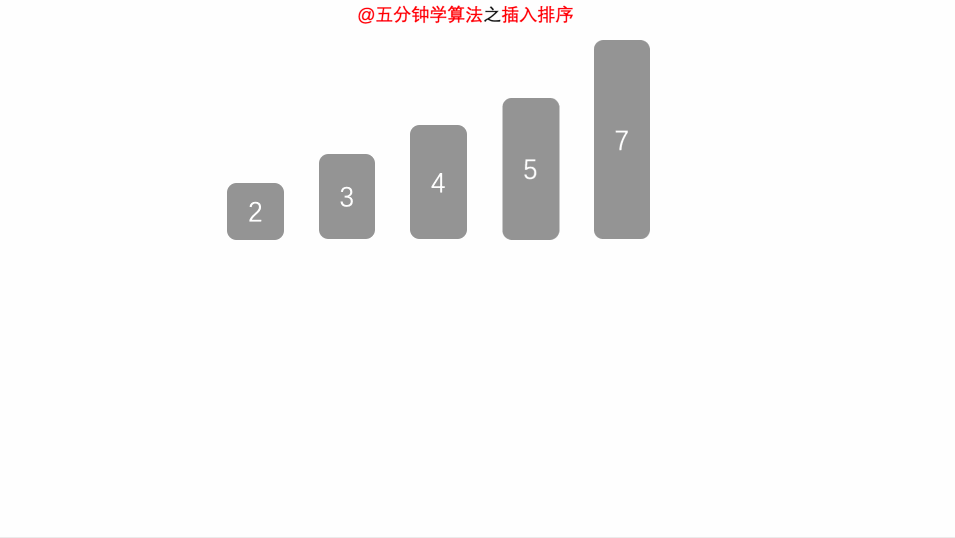
将序列分为有序部分和无序部分，从无序部分中依次选择元素，与有序部分进行比较，找到合适的位置，将原来的元素后移，将元素插入到相应的位置，直到全部记录插入完成。

动画演示

时间复杂度

1. 最好 — $O(n)$ 序列有序
2. 最坏 — $O(n^2)$ 序列逆序
3. 平均 — $O(n^2)$

空间复杂度 O（1）

1. 不带哨兵用临时变量temp
2. 带哨兵用a[0]

稳定性

稳定

适用性

1. 顺序表
2. 链表

算法特点

1. 稳定排序
2. 算法简易，易实现
3. 顺序表、链表均可实现
4. 更适用于初始记录基本有序的情况，当n较大时，时间复杂度高不宜采用。

核心代码

//直接插入排序（无哨兵） 
void InsertSort(int a[], int n){
    int i, j , temp;
    for(i = 1; i < n; i ++){
        if(a[i] < a[i - 1]){
            temp = a[i];
            for(j = i - 1; j >= 0 && temp < a[j]; j --){
                a[j + 1] = a[j];
            }
            a[j + 1] = temp;
        }
    }
}

//直接插入排序（有哨兵） 
void InsertSort2(int a[], int n){
    int i , j;
    for(i = 2; i <= n; i ++){
        if(a[i] < a[i - 1]){
            a[0] = a[i];
            for(j = i - 1; a[0] < a[j]; j --){
                a[j + 1] = a[j];
            }
            a[j + 1] = a[0];
        }
    }
} 

完整代码（无哨兵）

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <fstream>

using namespace std;
const int N = 10;
int data[N], idex;

//直接插入排序（无哨兵） 
void InsertSort(int a[], int n){
    int i, j , temp;
    for(i = 1; i < n; i ++){
        if(a[i] < a[i - 1]){
            temp = a[i];
            for(j = i - 1; j >= 0 && temp < a[j]; j --){
                a[j + 1] = a[j];
            }
            a[j + 1] = temp;
        }
    }
}

int main(){
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt",ios::in);
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt",ios::out);
    if (!infile.is_open()) { 
        cout << "Open file failure" << endl; 
    }
    while(!infile.eof()){
        infile >> data[idex ++];
    }

    //原数组元素 
    for(int i = 0; i < N; i ++) cout << data[i] << ' '; cout << endl;

    //不带哨兵的插入排序后 
    InsertSort(data,idex);
    for(int i = 0; i < N; i ++) cout << data[i] << ' '; cout << endl;

    for(int i = 0; i < N; i ++) outfile << data[i] << ' '; outfile << endl;

    infile.close();
    outfile.close();
    return 0;
} 

输入案例（in.txt）

13 69 86 99 59 23 64 32 86 72

输出结果(out.txt)

13 23 32 59 64 69 72 86 86 99

完整代码（有哨兵）

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <fstream>

using namespace std;
const int N = 20;
int data[N], idex,num = 10;

//直接插入排序（有哨兵） 
void InsertSort2(int a[], int n){
    int i , j;
    for(i = 2; i <= n; i ++){
        if(a[i] < a[i - 1]){
            a[0] = a[i];
            for(j = i - 1; a[0] < a[j]; j --){
                a[j + 1] = a[j];
            }
            a[j + 1] = a[0];
        }
    }
} 

int main(){
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt",ios::in);
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt",ios::out);
    if (!infile.is_open()) { 
        cout << "Open file failure" << endl; 
    }

    idex = 1;
    while(!infile.eof()){
        infile >> data[idex ++];
    }

    //原数组元素 
    for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;

    //不带哨兵的插入排序后 
    InsertSort2(data,num);
    //sort(data + 1 ,data + num + 1);
    for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;

    //输出排序后文件数据 
    for(int i = 1; i <= num; i ++)  outfile << data[i] << ' '; outfile << endl;

    infile.close();
    outfile.close();
    return 0;
} //直接插入排序（有哨兵）

输入案例（in.txt）

13 69 86 99 59 23 64 32 86 72

输出结果(out.txt)

13 23 32 59 64 69 72 86 86 99

返回排序算法目录

---

2. 折半插入排序

算法思想

设置三个变量 $low,high,mid，$令$mid = (low + high) / 2$,若 $a[mid] > key$, 则令$high = mid - 1$,否则令 $low = mid + 1$,直到 $low > hig$时停止循环。对序列中的每个元素做以上处理，找到合适位置将其他元素后移，进行插入。

时间复杂度

1. 最好 — $O(nlogn)$
2. 最坏 — $O(n^2)$
3. 平均 — $O(n^2)$

注：比较次数与待排序列的初始装态无关，仅取决于表中的元素个数

空间复杂度 O（1）

1. 不带哨兵用临时变量temp
2. 带哨兵用a[0]

稳定性

稳定

适用性

仅适用于顺序表

算法特点

1. 稳定排序
2. 因为要进行折半查找，所以只能用于顺序表，不能用于链表
3. 适合初始记录无序，n较大的情况。
4. 先比于直接插入排序，比较次数大大减少。

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;
int num, idx;//num存放元素个数 

int data[N]; 

//折半插入排序 (带哨兵) 
void BinaryInsertSort(int a[], int n){
    int i, j, low, high, mid;
    for(i = 2; i <= n; i ++){
        a[0] = a[i];//将带插入元素赋给哨兵
        low = 1, high = i - 1;//在1~i-1之间进行二分查找 
        while(low <= high){//high > low循环结束
         mid = low + high >> 1;
         if(a[0] < a[mid]) high = mid - 1;
         else low = mid + 1;//即便元素相等也插入其后，保持排序稳定性
        }
        for(j = i - 1; j >= high + 1; j --){// 待插元素应位于high+1处
         a[j + 1] = a[j];//将有序元素后移 
        }
        a[high + 1] = a[0];//将待插元素插入到正确位置
    }
}

int main(){
    //读文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt",ios::in);

    //写文件
    ofstream outfile; 
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt",ios::out);

    if(!infile.is_open()){//判断文件是否打开成功 
        cout << "file open failure !" << endl;
    }

    infile >> num;
    while(num != 0){
        infile >> data[++ idx];
        num --;
    }

    num = idx;
    for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;

    BinaryInsertSort(data, idx);
    //sort(data,data + num);
    for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl; 

    idx = 1;
    outfile << num; outfile << endl;
    while(num != 0){
        outfile << data[idx ++] << ' ';
        num --;
    }
    outfile << endl;

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
} 

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

返回排序算法目录

---

3. 希尔排序

算法思想

先将序列分为若干个子序列，然后对各个子序列进行直接插入排序，等到序列基本有序时，再对整个序列进行一次直接插入排序。即先追求表中的元素部分有序，再逐渐逼近全局有序。

优点：

让关键字值小的元素能能够很快移动到前面,且序列基本有序时进行直接插入排序时间效率会提升很多。

时间复杂度

1. 最好 — $无$
2. 最坏 — $O(n^2)$
3. 平均 — $O(n^{1.3})$

演示动画

空间复杂度 O（1）

使用数组头号元素a[0]

稳定性

不稳定

适用性

仅适用于顺序表

算法特点

1. 记录跳跃式地移动导致排序方法是不稳定的
2. 只能用于顺序结构，不能用于链式结构
3. 增量序列可以有各种取法，但应该使增量序列中的值没有除以以外的公因子，并且最后一个增量值必须为1
4. 记录总的比较次数和移动次数都比直接插入排序要少,n月大时，效果越明显。适合初始记录无序,n较大时的情况。

核心代码

//希尔排序 
void ShellSort(int a[], int n){
    int d, i, j;
    for(d = n / 2; d >= 1; d /= 2){//d为增量,增量序列依次折半(算法原创作者本人推荐) 
        for(i = d + 1; i <= n; i ++){//处理局部序列 
            if(a[i] < a[i - d]){
                a[0] = a[i];//暂存当前待处理元素 
                for(j = i - d; j > 0 && a[0] < a[j]; j -= d){
                    a[j + d] = a[j];//局部元素后移 
                }
                a[j + d] = a[0];//在合适位置处插入当前元素 
            }
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//希尔排序 
void ShellSort(int a[], int n){
    int d, i, j;
    for(d = n / 2; d >= 1; d /= 2){//d为增量,增量序列依次折半(算法原创作者本人推荐) 
        for(i = d + 1; i <= n; i ++){//处理局部序列 
            if(a[i] < a[i - d]){
                a[0] = a[i];//暂存当前待处理元素 
                for(j = i - d; j > 0 && a[0] < a[j]; j -= d){
                    a[j + d] = a[j];//局部元素后移 
                }
                a[j + d] = a[0];//在合适位置处插入当前元素 
            }
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[++ idx];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data + 1, data + 1 + idx); 
    for(int i = 1; i <= idx;  i++) cout << data[i] << ' '; cout << endl;

    ShellSort(data, idx);
    cout << "使用希尔排序后序列为：" << endl;
    for(int i = 1; i <= idx;  i++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 


    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

返回排序算法目录

---

四、 交换类排序

1. 冒泡排序

算法思想

从前往后（或从后往前）两两比较相邻元素的值,若为逆序则交换它们，直到序列比较完为止，称这样的过程为一趟冒泡排序，进行n-1趟冒泡排序即可完成排序。

注：

1. 每一趟排序都可以使一个元素移动到最终位置，已确定最终位置的元素在之后的处理中无需再对比
2. 如果某一趟排序过程中未发生交换，则算法可提前结束

时间复杂度

1. 最好 — $O(n)$ 有序序列
2. 最坏 — $O(n^2)$ 逆序序列
3. 平均 — $O(n^ {1.3})$

演示动画

空间复杂度

使用临时变量 ---- $O(1)$

稳定性

稳定

适用性

1. 顺序表
2. 链表

算法特点

1. 稳定排序
2. 可用于链式存储和顺序存储
3. 移动记录的次数比较多，算法平均时间性能比直接插入排序差。当初始序列无序，n 较大时，此算法不宜采用

核心代码

//冒泡排序 
void BubbleSort(int a[], int n){
    for(int i = 0; i < n - 1; i ++){// 控制趟数, n-1趟 
        bool flag = false;//标记每一趟是否有元素发生交换 
        for(int j = n - 1; j > i; j --){//从后往前依次枚举 
            if(a[j] < a[j - 1]){
            swap(a[j], a[j - 1]);
            flag = true;//发生交换 
            } 
        }
        if(flag == false) return;//本趟未发生交换,即所有元素都已经有序 
    }
}

优化历程

1.朴素写法

//升序排序
void bubble_sort(int a[], int len){//枚举趟, len为数组长度
    for(int i = 0; i < len; i ++){//枚举比较元素
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){//逆序,交换
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
            }
        }
    }
}

2.一次优化

设置一个标志位, 用来表示当前第 i 趟是否有交换, 如果有则要进行 i+1 趟, 如果没有, 则说明当前数组
已经完成排序, 一旦发现已经排好序, 立即跳出循环, 减少无谓的比较次数.

//升序排序
void bubble_sort(int a[], int len){
    for(int i = 0; i < len; i ++){
        bool flag = true;//记录是否发生交换
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){
                cnt ++;
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
                flag = false;//发生交换
            }
        }
        if(flag) break;//某一趟已经完全排好序,直接退出.
    }
}

3.二次优化

利用一个标志位, 记录一下当前第 i 趟所交换的最后一个位置的下标，在进行第 i+1趟的时候, 只需要内循
环到标记位置就可以了, 因为后面位置上的元素在上一趟中没有换位, 这一次也不可能会换位置了.

//升序排序
void bubble_sort(int a[], int len){
    int pos;
    for(int i = 0; i < len; i ++){
        bool flag = true;
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){
                cnt ++;
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
                pos = j;//记录交换的位置
                flag = false;//发生交换
            }
        }
        len = pos;//记录上一次已比较好的位置,用来更新 len
        if(flag) break;
    }
}

总结：

一次优化主要是针对在中间的某一次已经完全排好序,无需再进行后续比较的情况,增加一个标记,根据标记判断当
前数组是否已经完全排好序,一旦排好序,循环立即退出,减少了后续不必要的比较.

二次优化代码主要是在之前的基础上增加一个pos变量,用于记录上一趟发生交换元素最后一个位置,目的是略过之
前已经排好序的元素,枚举到未排好序的元素为止.

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//冒泡排序 
void BubbleSort(int a[], int n){
    for(int i = 0; i < n - 1; i ++){// 控制趟数, n-1趟 
        bool flag = false;//标记每一趟是否有元素发生交换 
        for(int j = n - 1; j > i; j --){//从后往前依次枚举 
            if(a[j] < a[j - 1]){
            swap(a[j], a[j - 1]);
            flag = true;//发生交换 
            } 
        }
        if(flag == false) return;//本趟未发生交换,即所有元素都已经有序 
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data, data + idx); 
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    BubbleSort(data, idx);
    cout << "使用冒泡排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

返回排序算法目录

---

2. 快速排序

算法思想

在待排序表 a[0...n-1]中任取一个元素pivot作为枢轴（或基准，通常取首元素）,通过一趟排序将待排序表划分为独立的两个部分a[0...k-1]和a[k + 1 ...n-1]，使得a[0...k-1]中的所有元素均小于pivot,a[k + 1...n - 1]中所有元素均大于等于pivot,则pivot放在其最终的位置a[k]上,这一过程成为一次“划分”，然后分别递归地对两个子表重复上述过程，直到每一部分内只有一个元素或空为止，即所有元素放在了其最终的位置上。

时间复杂度

1. 最好 — $O(nlogn)$ 序列均匀分割
2. 最坏 — $O(n^2)$ 序列有序
3. 平均 — $O(nlogn)$

演示动画

空间复杂度

1. 最好 — $O(nlogn)$ 序列均匀分割
2. 最坏 — $O(n)$ 序列有序

稳定性

不稳定

适用性

仅适用于顺序表

算法特点

1. 当n较大时，在平均情况下快速排序是所有内部排序方法中速度最快的一种，所以其适合初始记录无序、n较大时的情况
2. 记录非顺次的移动导致排序方法是不稳定的
3. 排序过程中需要定位表的上界和下界，所以仅适合于顺序结构，很难适用于链式结构

核心代码

//划分函数,选取枢轴元素,且定位数轴元素下标 
int Partion(int a[], int low, int high){
    int pivot = a[low];//选取第一个元素作为枢轴,当然也可以选最后一个元素作为枢轴
    while(low < high){//在low和high之间搜索枢轴位置 
        while(low < high && pivot <= a[high]) high --;
        a[low] = a[high];//比枢轴小的移动到左端 
        while(low < high && a[low] <= pivot) low ++;
        a[high] = a[low];//比枢轴大的移动到右端 
    }
    a[low] = pivot;//将枢轴存放到最终位置 
    return low;//返回存放枢轴的最终的位置 
} 

//快速排序 
void QuickSort(int a[], int low, int high){
    if(low < high){//递归跳出条件 
        int pivotpos = Partion(a, low, high);//划分 
        QuickSort(a, low, pivotpos - 1);//划分左子表 
        QuickSort(a, pivotpos + 1, high);//划分右子表 
    }
}

精简代码

void quick_sort(int q[], int l, int r)
{
    if(l >= r)   return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j)   swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

注：

此乃 y 总毕生锤炼之精华，全网最简，没有之一，哈哈....

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//划分函数,选取枢轴元素,且定位数轴元素下标 
int Partion(int a[], int low, int high){
    int pivot = a[low];//选取第一个元素作为枢轴 
    while(low < high){//在low和high之间搜索枢轴位置 
        while(low < high && pivot <= a[high]) high --;
        a[low] = a[high];//比枢轴小的移动到左端 
        while(low < high && a[low] <= pivot) low ++;
        a[high] = a[low];//比枢轴大的移动到右端 
    }
    a[low] = pivot;//将枢轴存放到最终位置 
    return low;//返回存放枢轴的最终的位置 
} 

//快速排序 
void QuickSort(int a[], int low, int high){
    if(low < high){//递归跳出条件 
        int pivotpos = Partion(a, low, high);//划分 
        QuickSort(a, low, pivotpos - 1);//划分左子表 
        QuickSort(a, pivotpos + 1, high);//划分右子表 
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data, data + idx); 
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    QuickSort(data, 0, idx - 1);
    cout << "使用快速排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

经典例题

快速排序

返回排序算法目录

---

五、 归并类排序

1. 归并排序

算法思想

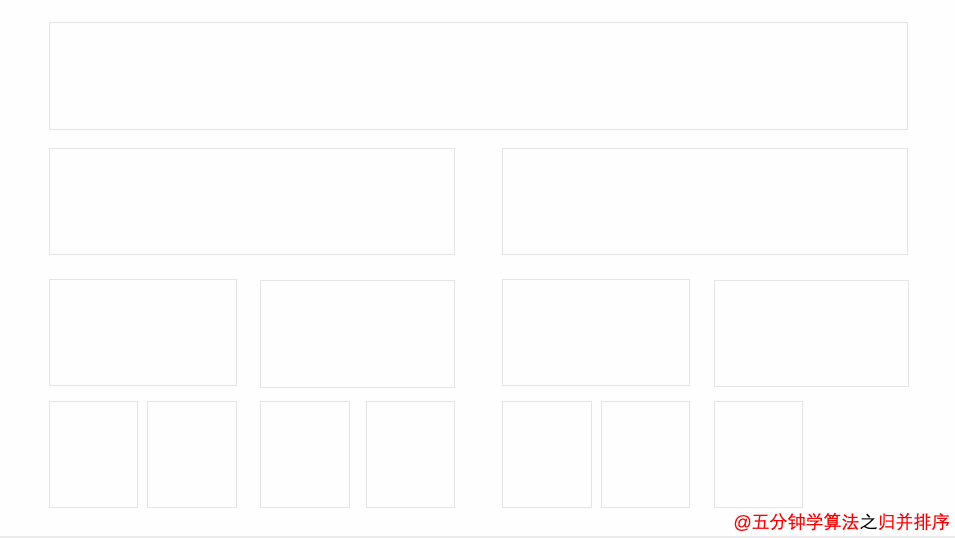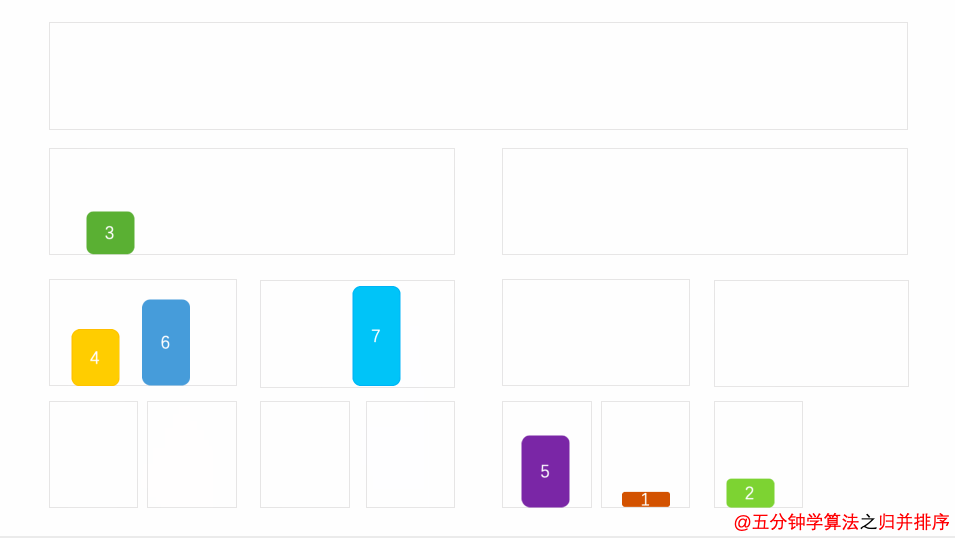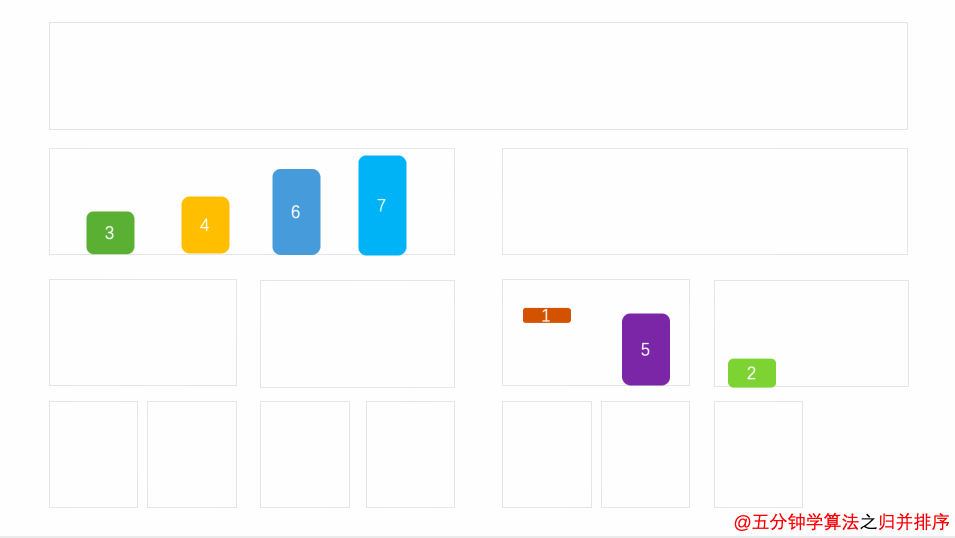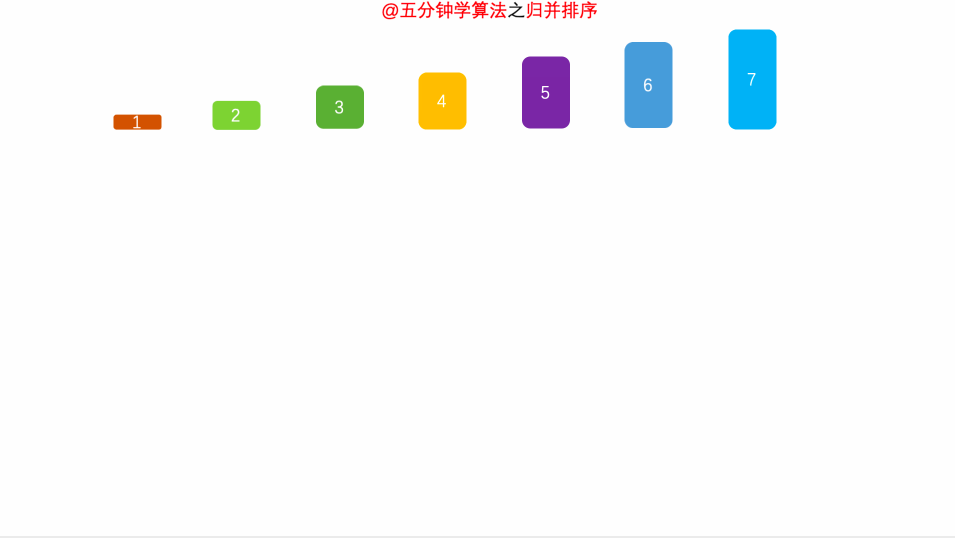
将两个或多个有序序列合并为一个有序序列

注：

1. 二叉树的第 h 层最多有 2^h-1^ 个结点，若树高为 h ，则应该满足 n <= 2^h-1^ , 即 $h - 1 = \lceil log{_2}n\rceil$, 即趟数 = $\lceil log{_2}n\rceil$
2. 每趟归并时间复杂度为 $O(n)$ ,则算法时间复杂度为 $O(nlogn)$
3. 空间复杂度为 $O(n)$ ,来自于辅助数组

时间复杂度

1. 最好 — $O（nlogn）$
2. 最坏 — $O(nlogn)$
3. 平均 — $O（nlogn）$

注：

归并排序分割子序列与初始序列无关，因此它的最好、最坏、平均时间复杂度均为 $O（nlogn）$

演示动画

空间复杂度

需要一个辅助数组 ---- $O（n）$

稳定性

稳定

适用性

1. 顺序表
2. 链表

算法特点

1. 稳定排序
2. 可用于顺序结构，也可用于链式结构。使用链式结构不需要附加的存储空间，但递归实现时仍需要开辟相应的递归工作栈。
3. 一般而言，对于 $n$ 个元素进行 $k$ 路归并排序时，排序的趟数 $m$ 满足 $k^m = n$, 从而 $m = log{_k}n$ ，又考虑到 $m$为整数，所以$m = \lceil log{_k}n\rceil$

核心代码

//a[low ... mid] 和 a[mid + 1 ...high]各自有序,将二者归并 
void Merge(int a[], int low, int mid, int high){
    int k = low;
    int i = low, j = mid + 1;//左、右部分首元素 

    //将 a数组数据复制到 b数组 
    for(int i = low; i <= high; i ++) b[i] = a[i];

    //将 a[low ... mid] 和 a[mid + 1 ...high]归并
    while(i <= mid && j <= high){ 
        if(b[i] < b[j]) a[k ++] = b[i ++];
        else a[k ++] = b[j ++];
    }

    while(i <= mid) a[k ++] = b[i ++];//a数组已经枚举完 
    while(j <= high) a[k ++] = b[j ++];//b数组已经枚举完
}  

// 归并排序 
void MergeSort(int a[], int low, int high){//a[low ...high]
    if(low < high){
        int mid = low + high >> 1;//从中间划分 
        MergeSort(a, low, mid);//对左半部分进行归并排序 
        MergeSort(a, mid + 1, high);//对左半部分进行归并排序 
        Merge(a, low, mid, high);//归并 
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx, b[N];

//a[low ... mid] 和 a[mid + 1 ...high]各自有序,将二者归并 
void Merge(int a[], int low, int mid, int high){
    int k = low;
    int i = low, j = mid + 1;//左、右部分首元素 

    //将 a数组数据复制到 b数组 
    for(int i = low; i <= high; i ++) b[i] = a[i];

    //将 a[low ... mid] 和 a[mid + 1 ...high]归并
    while(i <= mid && j <= high){ 
        if(b[i] < b[j]) a[k ++] = b[i ++];
        else a[k ++] = b[j ++];
    }

    while(i <= mid) a[k ++] = b[i ++];//a数组已经枚举完 
    while(j <= high) a[k ++] = b[j ++];//b数组已经枚举完
}  

// 归并排序 
void MergeSort(int a[], int low, int high){//a[low ...high]
    if(low < high){
        int mid = low + high >> 1;//从中间划分 
        MergeSort(a, low, mid);//对左半部分进行归并排序 
        MergeSort(a, mid + 1, high);//对左半部分进行归并排序 
        Merge(a, low, mid, high);//归并 
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data, data + idx ); //sort排序区间左闭右开 
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    MergeSort(data, 0, idx - 1);
    cout << "使用堆排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

返回排序算法目录

---

六、选择类排序

1. 简单选择排序

算法思想

每一趟在待排元素中选取关键字最小的元素加入到有序序列

注：

简单选择排序与序列的初始状态无关，仅与序列的元素个数有关

时间复杂度

1. 最好 — $O（n^2）$
2. 最坏 — $O(n^2)$
3. 平均 — $O（n^2）$

演示动画

空间复杂度

仅用一个临时变量 min — $O（1）$

稳定性

不稳定

适用性

1. 顺序表
2. 链表

算法特点

1. 不稳定，但改变策略可以写出不产生“不稳定现象”的选择排序算法
2. 可用于链式存储结构
3. 移动次数较少，当每一记录占用的空间较多时，此方法比直接插入排序快
4. 选择排序的主要操作是关键字的比较，因此，改进此算法应从减少“比较次数”出发考虑

核心代码

//交换两个元素 
void swap(int &a, int &b){
    int temp = a;
    a = b;
    b = temp;
}

//选择排序 
void SelectSort(int a[], int n){
    for(int i = 0; i < n; i ++){
        int min = i;//min记录最下元素的下标 
        for(int j = i; j < n; j ++){
            if(a[j] < a[min]) min = j;
        }
        if(min != i) swap(a[i], a[min]);//交换两个值 
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//交换两个元素 
void swap(int &a, int &b){
    int temp = a;
    a = b;
    b = temp;
}

//选择排序 
void SelectSort(int a[], int n){
    for(int i = 0; i < n; i ++){
        int min = i;//min记录最下元素的下标 
        for(int j = i; j < n; j ++){
            if(a[j] < a[min]) min = j;
        }
        if(min != i) swap(a[i], a[min]);//交换两个值 
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data, data + idx); 
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    SelectSort(data, idx);
    cout << "使用选择排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

返回排序算法目录

---

2. 堆排序

算法思想

每一趟将堆顶元素加入到有序子序列（与待排元序列中的最后一个元素交换），并将待排序列再次调整为大根堆（即将小元素 “下坠” ）。

注：

1. 基于 “大根堆” 的堆排序得到的是递增序列
2. 一个结点每“下坠”一层，最多只需要比对关键字两次
3. 若树高为h，某结点在第i层，将这个结点向下调整最多只需要“下坠”h - i层，关键字的比对次数不超过2(h - i)
4. n个结点的完全二叉树，树高 $h = \lfloor log{_2}n \rfloor + 1$

时间复杂度

1. 最好 — $O（nlogn）$
2. 最坏 — $O(nlogn)$
3. 平均 — $O（nlogn）$

注：时间复杂度 = O(n) + O(nlog_2n) = O(nlogn)

演示动画

空间复杂度

$O（1）$

稳定性

不稳定

适用性

仅适用于顺序表

算法特点

1. 不稳定排序
2. 只能用于顺序结构，不能用于链式结构
3. 初始建堆所需要的比较次数比较多。因此，当记录数较少时，不宜采用。当记录较多时，较为高效。

核心代码

1. 建大根堆思路

把所有非终端结点都检查一遍，是否满足大根堆的要求，如果不满足，则进行调整：
1. 检查当前结点是否满足根 >= 左、右，如果不满足，则将当前结点与更大的一个孩子交换
2. 若元素互换破坏了下一级的堆，则采用相同的方式继续往下调整（小元素不断“下坠”）

//将以k为根结点的树调整为大根堆 
void HeadAdjust(int a[], int k, int len){//注：除k结点外其他已经有序 
    a[0] = a[k];//a[0]暂存子树根节点 
    for(int i = 2 * k; i <= len; i *= 2){//沿较大子结点筛选 
        if(i < len && a[i] < a[i + 1]) i ++;//i为较大子结点下标 （i<len表示k有右孩子） 
        if(a[0] >= a[i]) break;//筛选结束 
        else{
            a[k] = a[i];//递归处理子结点 
            k = i;
        }
    }
    a[k] = a[0];
}

//建大根堆 时间复杂度---O(n)  
void BuildHeap(int a[], int len){//从下往上建堆,从最后一个叶子结点的根节点开始 
    for(int i = len / 2; i > 0; i --){//处理所有非终端结点 
        HeadAdjust(a, i , len);
    }
}//建堆过程关键字的比较次数不超过4n(定理) 

2. 堆排序思路

每一趟将堆顶元素加入到有序子序列(与待排列中的最后一个元素交换)，并将待排序列再次调整为大根堆(小元素不断“下坠”)

//堆排序的完整逻辑 
void HeapSort(int a[], int len){
    BuildHeap(a, len);//建堆 O(n) 
    for(int i = len; i > 1; i --){//从后往前处理 ,共n-1趟交换和调整 
        swap(a[i], a[1]);//将堆顶元素(最大元素)与堆底元素交换 
        HeadAdjust(a, 1, i - 1);//把剩余待排元素调整为堆 
    }
}//每趟时间复杂度不超过o(h) =  O(logn),共 n-1趟 

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//将以k为根结点的树调整为大根堆 
void HeadAdjust(int a[], int k, int len){//注：除k结点外其他已经有序 
    a[0] = a[k];//a[0]暂存子树根节点 
    for(int i = 2 * k; i <= len; i *= 2){//沿较大子结点筛选 
        if(i < len && a[i] < a[i + 1]) i ++;//i为较大子结点下标 （i<len表示k有右孩子） 
        if(a[0] >= a[i]) break;//筛选结束 
        else{
            a[k] = a[i];//递归处理子结点 
            k = i;
        }
    }
    a[k] = a[0];
}

//建大根堆 时间复杂度---O(n)  
void BuildHeap(int a[], int len){//从下往上建堆,从最后一个叶子结点的根节点开始 
    for(int i = len / 2; i > 0; i --){//处理所有非终端结点 
        HeadAdjust(a, i , len);
    }
}//建堆过程关键字的比较次数不超过4n(定理) 

//堆排序的完整逻辑 
void HeapSort(int a[], int len){
    BuildHeap(a, len);//建堆 O(n) 
    for(int i = len; i > 1; i --){//从后往前处理 ,共n-1趟交换和调整 
        swap(a[i], a[1]);//将堆顶元素(最大元素)与堆底元素交换 
        HeadAdjust(a, 1, i - 1);//把剩余待排元素调整为堆 
    }
}//每趟时间复杂度不超过o(h) =  O(logn),共 n-1趟 

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[++ idx];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data + 1, data + 1 + idx); 
    for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;

    HeapSort(data, idx);
    cout << "使用堆排序后序列为：" << endl;
    for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

9. 计数排序

算法思想

首先,扫描一下整个原始序列 $a$，获取最小值 $min$ 和最大值 $max$，其次开辟一块新的存储空间 $b [ d ]$,该数组长度为 $d = max - min + 1$，$b[d]$中存储的是在min ~ max之间的相应数值出现的次数，如：$b[5] = 2$,表示 $5$ 出现 $2$ 次，最后根据 $b$ 数组的统计的元素次数,依次输出各元素。

inference

时间复杂度

1. 最好 — $O(n + m)$
2. 最坏 — $O(n + m)$
3. 平均 — $O(n + m)$

演示动画

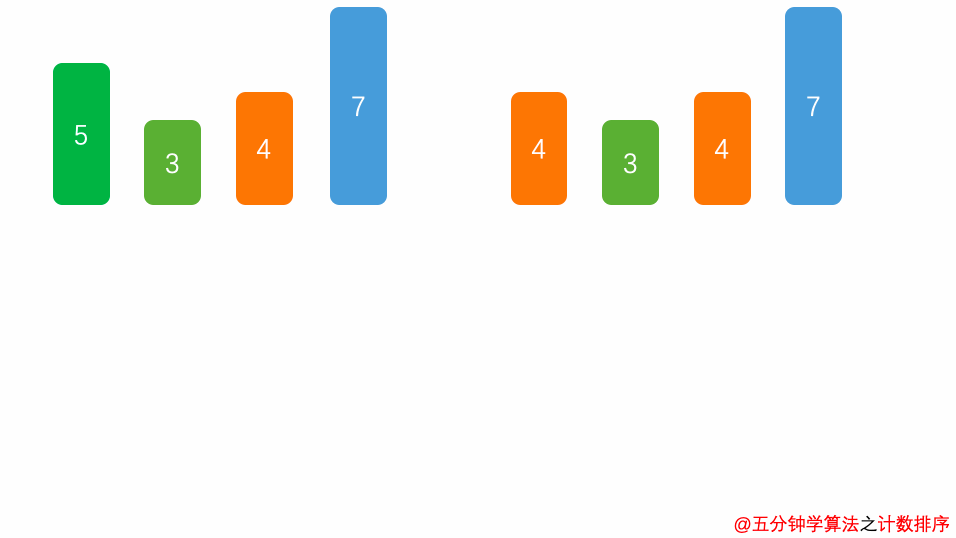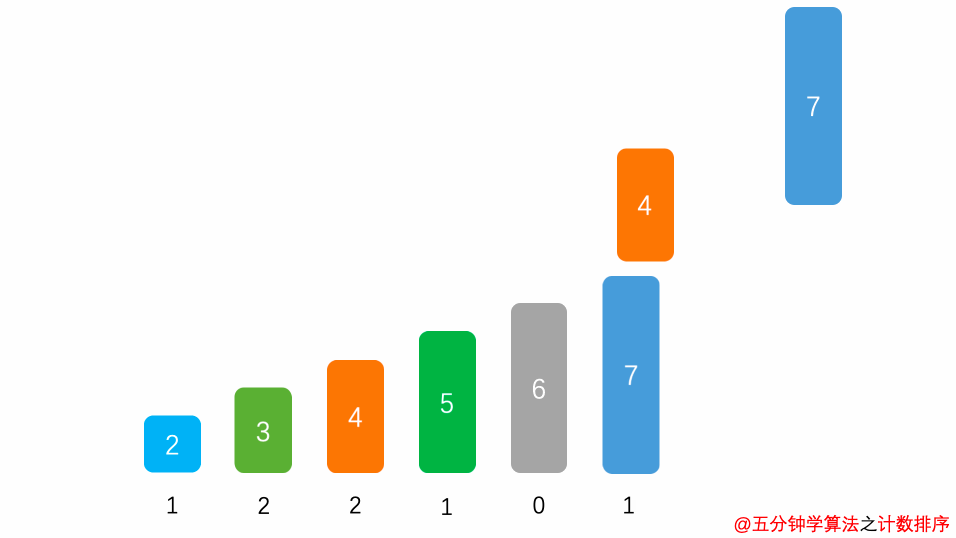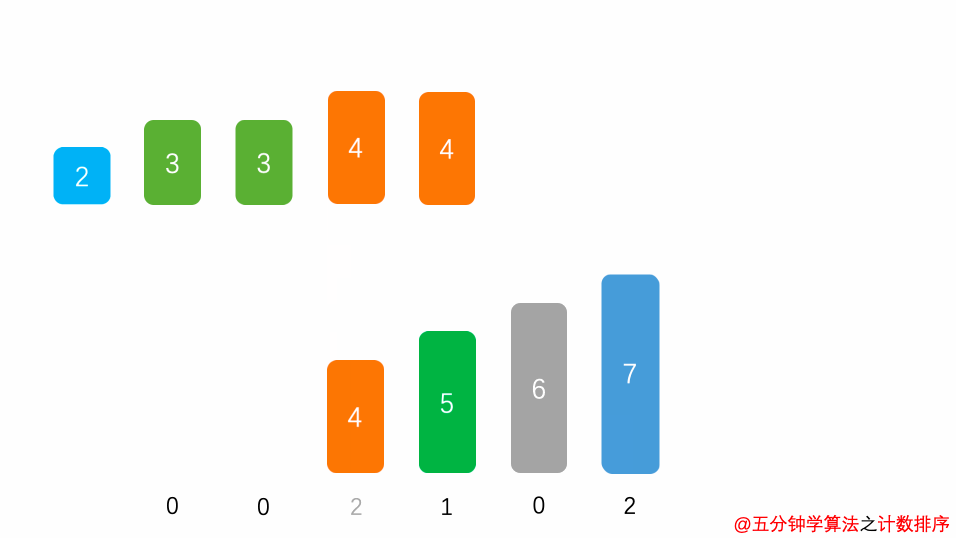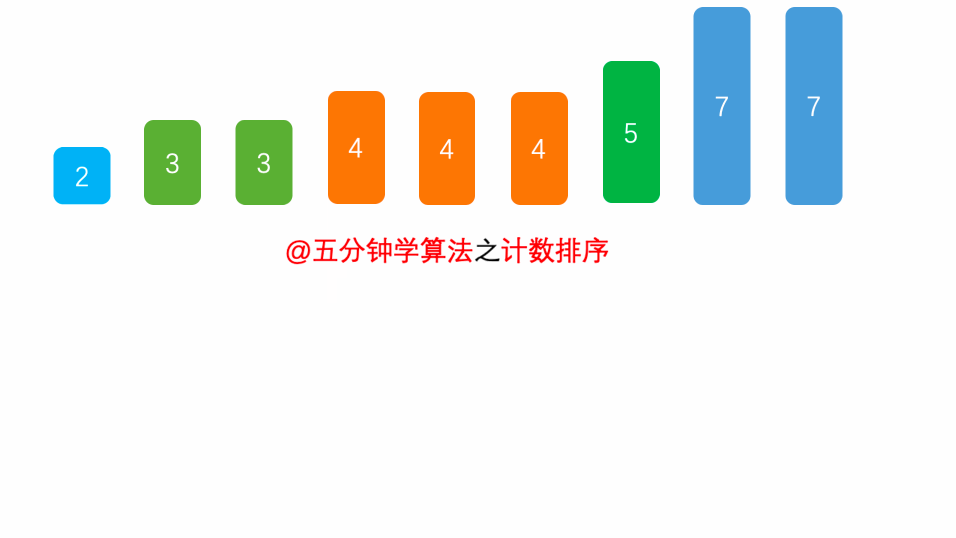
空间复杂度

$O(m)$

稳定性

稳定、不稳定均可设定

算法特点

1.当数列最大最小值差距过大时，并不适用计数排序。

比如给定20个随机整数，范围在0到1亿之间，这时候如果使用计数排序，需要创建长度1亿的数组。不但严重浪费空间，而且时间复杂度也随之升高。

2.当数列元素不是整数，并不适用计数排序。

如果数列中的元素都是小数，比如25.213，或是0.00000001这样，则无法创建对应的统计数组。这样显然无法进行计数排序。

算法适用性

1. 顺序表
2. 链表

朴素版特点

1. 代码简洁、易实现
2. 由于根据最大值开辟存储空间,可能造成空间的浪费,因此耗费存储空间大
3. 无法保证元素的稳定性

核心代码

//朴素版 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int cnt[maxval + 1] = {0};//根据最大值开辟新数组空间 

    for(int i = 0; i < n; i ++) cnt[a[i]] ++;//统计原数组中元素出现的次数 

    for(int i = minval, k = 0; i <= maxval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//朴素版 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int cnt[maxval + 1] = {0};//根据最大值开辟新数组空间 

    for(int i = 0; i < n; i ++) cnt[a[i]] ++;//统计原数组中元素出现的次数 

    for(int i = minval, k = 0; i <= maxval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

---

一次优化特点

1. 相比于朴素版, 空间复杂度大大降低
2. 不能保证稳定性

核心代码

//一次优化 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    for(int i = 0, k = 0; i <= maxval - minval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i + minval;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//一次优化 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    for(int i = 0, k = 0; i <= maxval - minval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i + minval;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

---

二次优化特点

1. 相比于朴素版, 空间复杂度大大降低
2. 可以保证稳定性，该排序稳定

核心代码

//二次优化 
void CountSort(int a[], int n){
    //遍历数组求得最大值和最小值
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){ 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    int sum = 0;
    for(int i = 0; i < d; i ++){//本质为前缀和数组,用于求位次 
        sum += cnt[i];//此处的cnt既为元素又为之前的元素和,即cnt[i] = cnt[i] + cnt[i - 1] 
        cnt[i] = sum;// 比如, cnt[5] = 3,表示分数95, 排名第 3 
    } 

    int sortArray[d];//sortArray[]存元素真实序列 
    for(int i = n - 1; i >= 0; i --){//将原数组元素从后往前遍历 
        sortArray[cnt[a[i] - minval] - 1] = a[i];
        cnt[a[i] - minval] --;
    }

    //将排序后的序列赋给原数组
    for(int i = 0, k = 0; i < d; i ++){
        data[k ++] = sortArray[i];
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//二次优化 
void CountSort(int a[], int n){
    //遍历数组求得最大值和最小值
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){ 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    int sum = 0;
    for(int i = 0; i < d; i ++){//本质为前缀和数组,用于求位次 
        sum += cnt[i];//此处的cnt既为元素又为之前的元素和,即cnt[i] = cnt[i] + cnt[i - 1] 
        cnt[i] = sum;// 比如, cnt[5] = 3,表示分数95, 排名第 3 
    } 

    int sortArray[d];//sortArray[]存元素真实序列 
    for(int i = n - 1; i >= 0; i --){//将原数组元素从后往前遍历 
        sortArray[cnt[a[i] - minval] - 1] = a[i];
        cnt[a[i] - minval] --;
    }

    //将排序后的序列赋给原数组
    for(int i = 0, k = 0; i < d; i ++){
        data[k ++] = sortArray[i];
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

10.桶排序

---

算法思想

首先, 遍历原始序列确定最大值 $maxval$ 和最小值 $minval$，并确定桶的个数 $n$; 然后，将待排序集合中处于同一个值域的元素存入同一个桶中,在桶内使用各种现有的算法进行排序; 最后按照从小到大的顺序依次收集桶中的每一个元素, 即为最终结果。

inference
inference

时间复杂度

1. 最好 — $O(n + k)$
2. 最坏 — $O(n^2)$
3. 平均 — $O(n + k)$

注： $其中 k = nlog(n / m)$

演示动画

空间复杂度

$O(n + k)$

注： $其中 k = nlog(n / m)$

稳定性

稳定

算法特点

1. 桶排序是一种用空间换取时间的排序
2. 桶排序并非像常规排序那样没有限制，桶排序有相当的限制。因为桶的个数和大小都是我们人为设置的。而每个桶又要避免空桶的情况。所以我们在使用桶排序的时候即需要对待排序数列要求偏均匀，又要要求桶的设计兼顾效率和空间。
3. 数要相对均匀分布，桶的个数也要合理设计。在设计桶排序时，需要知道输入数据的上界和下界，根据数据的分布情况考虑是否用桶排序，当然如果能用好桶排序，效率还是很高的！

算法适用性

顺序表

核心代码

//桶排序 
void BucketSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//寻找原序列数组元素的最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int bnum = 10;//桶中元素个数 
    int m = (maxval - minval) / bnum + 1;//桶的个数 
    vector< vector<int> > bucket(m);

    //收集,将元素入相应的桶中. 减偏移量是为了将元素映射到更小的区间内,省内存 
    for(int i = 0; i < n; i ++) bucket[(a[i] - minval) / bnum].push_back(a[i]);

    //将桶内元素排序 
    for(int i = 0; i < m; i ++) sort(bucket.begin(), bucket.end());

    //收集, 将各个桶中的元素收集到一起 
    for(int i = 0, k = 0; i < m; i ++){
        for(int j = 0; j < bucket[i].size(); j ++){
            data[k ++] = bucket[i][j];
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>
#include <vector>

using namespace std;
const int N = 200;

int data[N], num, idx; 

//桶排序 
void BucketSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//寻找原序列数组元素的最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int bnum = 10;//桶中元素个数 
    int m = (maxval - minval) / bnum + 1;//桶的个数 
    vector< vector<int> > bucket(m);

    //收集,将元素入相应的桶中. 减偏移量是为了将元素映射到更小的区间内,省内存 
    for(int i = 0; i < n; i ++) bucket[(a[i] - minval) / bnum].push_back(a[i]);

    //将桶内元素排序 
    for(int i = 0; i < m; i ++) sort(bucket.begin(), bucket.end());

    //收集, 将各个桶中的元素收集到一起 
    for(int i = 0, k = 0; i < m; i ++){
        for(int j = 0; j < bucket[i].size(); j ++){
            data[k ++] = bucket[i][j];
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    BucketSort(data, idx);
    cout << "使用桶排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

---

谢谢观看, 多多点赞, 您的支持就是我持续的动力！

---

返回排序算法目录

---