单调栈

例题题意：求出每个元素的左边离它最近且比它小的元素。
Code:

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10; 
int a[N], l[N], stk[N], top; //stk中存储的是下标 
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
    }

    for(int i = 1; i <= n; i ++)
    {
        while(top && a[stk[top]] >= a[i]) top --;

        if(top) l[i] = a[stk[top]];
        else l[i] = -1;

        stk[++ top] = i;
    }
    for(int i = 1; i <= n; i ++) cout << l[i] << " ";
    return 0;   
}

单调队列

例题题意：求出滑动窗口中的最大元素和最小元素。
Code

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10; 
int n, k;
int q[N], a[N], tt = 0, hh = 1; // 数组模拟队列，tt为队尾，hh为队头，当hh>=tt时队列为非空，q中存储的是下标 
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> k;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
    }

    //求最大
    for(int i = 1; i <= n; i ++)
    {
      //以i为右端点，大小为k的区间[i - k + 1, k]
      //判断队头的合法性
      while(hh <= tt && q[hh] < i - k + 1) hh ++;

      //判断队尾优越性
      while(hh <= tt && a[q[tt]]<= a[i]) tt --;

      //入队
      q[++ tt] = i;

      if(i >= k) cout << a[q[hh]] << " ";   
    } 
    cout << endl;
    tt = 1, hh = 0;
    //求最小
    for(int i = 1; i <= n; i ++)
    {
        while(hh <= tt && q[hh] < i - k + 1) hh ++;
        while(hh <= tt && a[q[tt]] >= a[i]) tt --;
        q[++ tt] = i;
        if(i >= k) cout << a[q[hh]] << " ";
    } 
    return 0;   
}

求组合数1

Code:

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
typedef long long int LL;
const int N = 2010, mod = 1e9+7;
int n;
int c[N][N];
void init(){
    for(int i = 0; i < N; i ++ )
      for(int j = 0; j <= i; j++ )
        if(!j) c[i][j] = 1; //如果j为0就只有一种方案数，初始化为1
        else c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod; //组合数递推式
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);//可以提高cin读入的速度，但是写了后cin不能和scanf一起用
  cin>>n;
  init();
  while(n--){
      int a, b;
      cin >> a >> b;
      cout<< c[a][b] << endl;
  }
}

求组合数2

Code：

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e7 + 10, p = 1e9 + 7; 
LL fac[N]; //阶乘数组 

LL qmi(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1)
        {
            res = res * a % p;
        }
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

LL inv(LL x) //求逆元函数 
{
    return qmi(x, p - 2);
}

LL C(LL n, LL m) //求组合数 
{
    if(n < 0 || m < 0 || m > n) return 0;
    return fac[n] * inv(fac[m]) % p * inv(fac[n - m]) % p;
}

void init() //初始化阶乘数组 
{
    fac[0] = 1;
    for(int i = 1; i <= 1e7; i ++)
    {
        fac[i] = fac[i - 1] * i % p;
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    init(); 
    int q;
    cin >> q;
    while(q --)
    {
        int a, b;
        cin >> a >> b;
        cout << C(a, b) << endl; 
    }

    return 0;   
}

离散化

例题题意，在一个下标很大的范围对相应下标的位置的数进行加，再询问区间和
Code

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5 + 10, p = 1e9 + 7; 
struct Q{
    int a, b;
}add[N], que[N];
vector<int> X; //离散化数组 
int a[N * 3]; //存储离散化之后的数组 
int n, q;

int getidx(int x) //返回映射之后的下标 
{
    //下标映射范围是[1, X.size()] 
    return lower_bound(X.begin(), X.end(), x) - X.begin() + 1; 
} 
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++)
    {
        int x, w;
        cin >> x >> w;
        add[i] = {x, w};
        X.push_back(x); 
    }

    for(int i = 1; i <= q; i ++)
    {
        int l, r;
        cin >> l >> r;
        que[i] = {l, r};
        X.push_back(l);
        X.push_back(r);
    }
    //对离散化数组排序去重 
    sort(X.begin(), X.end());
    X.erase(unique(X.begin(), X.end()), X.end());

    for(int i = 1; i <= n; i ++)
    {
       int ux = add[i].a;
       int w = add[i].b;
       a[getidx(ux)] += w;  
    } 

    for(int i = 1; i <= X.size(); i ++) a[i] += a[i - 1]; //求前缀和
    for(int i = 1; i <= q; i ++)
    {
       int tl = getidx(que[i].a);
       int tr = getidx(que[i].b);
       cout << a[tr] - a[tl - 1] << endl;   
    } 
    return 0;    
 }

树状数组

单点修改，区间查询 Code：

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, p = 1e9 + 7; 
int n, q; 
LL a[N], t[N];
//树状数组模板 
int lowbit(int x)
{
    return x & -x;
}
void add(int k, int x)  //对树状数组进行单点修改 
{
    for(int i = k; i <= n; i += lowbit(i)) t[i] += x;
}

LL getsum(int x)
{
    LL res = 0;
    for(int i = x; i > 0; i -= lowbit(i)) res += t[i];
    return res;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    for(int i = 1; i <= n; i ++)
    {
        add(i, a[i]);
    }

    while(q --)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int k, x;
            cin >> k >> x;
            add(k, x);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << getsum(r) - getsum(l - 1) << endl;
        }
    }
    return 0;    
 }

区间修改，区间查询

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, p = 1e9 + 7; 
int n, q; 
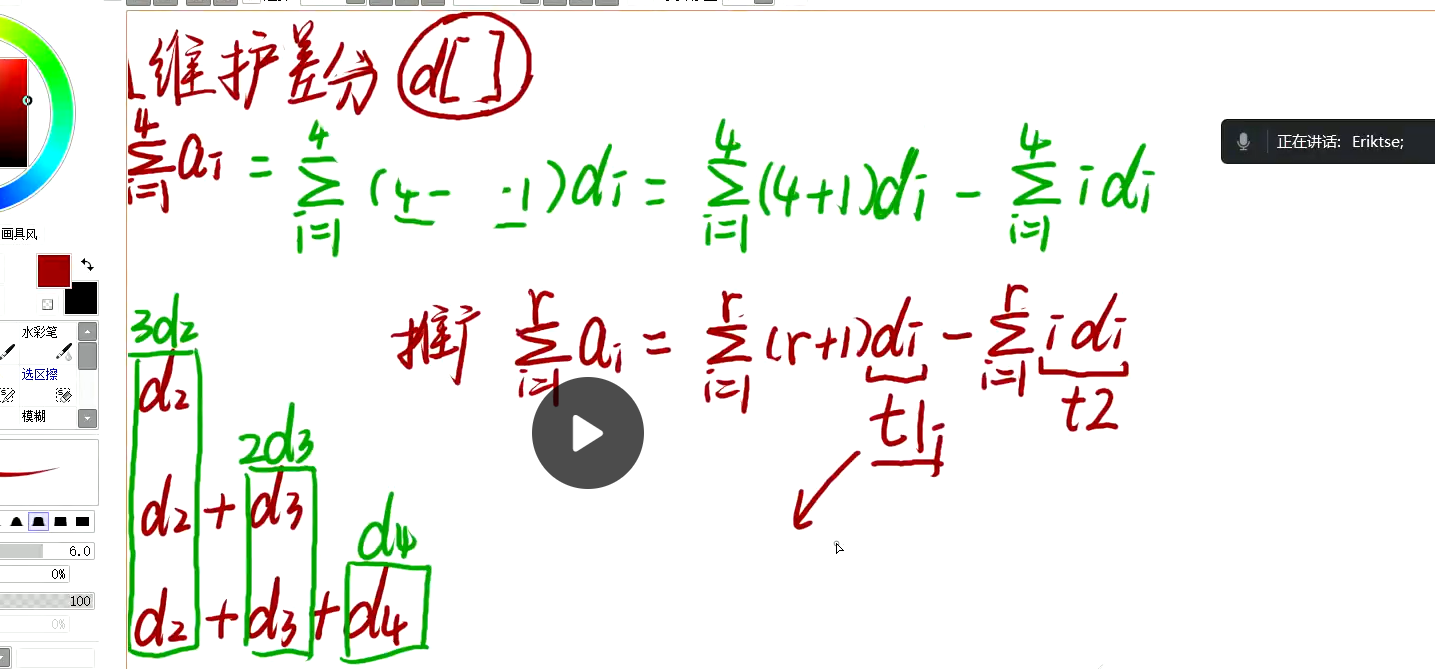
LL a[N], td[N], tdi[N]; //td维护差分数组d的树状数组，tdi则维护i*d的树状数组，两个树状数组跟据公式维护区间和 
//树状数组模板 
int lowbit(int x)
{
    return x & -x;
}
void add(LL k, LL x)  //对树状数组进行单点修改 
{
    for(int i = k; i <= n; i += lowbit(i)) td[i] += x, tdi[i] += x * k;
}

LL getsum(LL x)
{
    LL res = 0;
    for(int i = x; i > 0; i -= lowbit(i)) res += (x + 1) * td[i] - tdi[i];
    return res;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    for(int i = 1; i <= n; i ++)
    {
        add(i, a[i]),  add(i + 1, -a[i]);
    }

    while(q --)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            LL l, r, v;
            cin >> l >> r >> v;
            add(l, v), add(r + 1, -v);
        }
        else
        {
            LL l, r;
            cin >> l >> r;
            cout << getsum(r) - getsum(l - 1) << endl;
        }
    }
    return 0;    
 }

树状数组求逆序对

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, p = 1e9 + 7; 
//离散化 + 树状数组求逆序对  
int a[N], t[N], n;
vector<int> X;

int getidx(int x)
{
    return lower_bound(X.begin(), X.end(), x) - X.begin() + 1;
}

int lowbit(int x)
{
    return x & -x;
}

void add(int k, int x)
{
    for(int i = k; i <= X.size(); i += lowbit(i)) 
    {
        t[i] += x;
    }
}

int getsum(int r)
{
    int res = 0;
    for(int i = r; i > 0; i -= lowbit(i)) res += t[i];
    return res;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
        X.push_back(a[i]);
    }

    sort(X.begin(), X.end());
    X.erase(unique(X.begin(), X.end()), X.end());
    LL ans = 0;
    for(int i = 1; i <= n; i ++)
    {
        //求下标比当前数的下标小，并且数值比当前数大的数字的数量
        ans += getsum(X.size()) - getsum(getidx(a[i]));
        add(getidx(a[i]), 1); //把当前数的映射加入树状数组 
    }

    cout << ans << endl;
    return 0;    
 }

带懒标记的加法线段树

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, M = N * 3; 
//t为线段树数组，lz为懒标记数组 
LL a[N], t[N << 2], lz[N << 2]; //开4倍空间，t[x]表示结点x所表示的区间的元素之和
//lz[o]表示：结点o还有lazy[o]这么大的一个数字，还没加给左右儿子
int n, q;

//pushup就是用儿子的信息来更新自己的信息
void pushup(int o)
{
    t[o] = t[o << 1] + t[o << 1 | 1];
}


void pushdown(int s, int e, int o)
{
    if(!lz[o]) return; //如果lz[o] == 0，无需下放

    int mid = (s + e) >> 1;
    //ls表示左儿子编号，rs表示右儿子编号
    int ls = o << 1, rs = o << 1 | 1;
    //注意此处的lazy传递是重点！
    //lz[o]表示区间每个点都要加上lz[o]
    //于是对于t（区间和）来说要乘上一个区间长度

    t[ls] += (mid - s + 1) * lz[o];
    t[rs] += (e - mid) * lz[o];

    //标记也要下放
    lz[ls] += lz[o];
    lz[rs] += lz[o];
    //lazytag下放完毕
    lz[o] = 0;
}
void buildtree(int s = 1, int e = n, int o = 1)
{
    if(s == e)
    {
        t[o] = a[s];
        return;
    } 

    //递归建左右子树
    int mid = (s + e) >> 1;
    buildtree(s, mid, o << 1);
    buildtree(mid + 1, e, o << 1 | 1);
    pushup(o);
}

void add(int l, int r, LL x, int s = 1, int e = n, int o = 1) //初始化参数时候要记得将后面的参数赋为一个默认参数值 
{

    if(s >= l && e <= r)
    {
    //当前操作区间已经完全进入目标区间
    //当前节点信息应当直接被修改并打上lz标记，不再往下走
       t[o] += (e - s + 1) * x;
    //到当前节点时，t[o]为正确的值，lz[o]不一定为0
    //所以lz[o]不能直接赋值，而应该加上x
       lz[o] += x;  
       return;
    } 

     //向下走之前，一定要pushdown
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    //判断是否需要向左走，如果左儿子区间[s, mid]和[l, r]有交集，就要走
    //注意这里无需判断s <= r，因为这是必然的
    //如果s > r，那么当前节点都进不来
    if(mid >= l) add(l, r, x, s, mid, o << 1);
    //判断是否需要向右走，如果右儿子区间[mid+1,e]和[l, r]有交集，就要走
    if(mid + 1 <= r) add(l, r, x, mid + 1, e, o << 1 | 1); 

    //递归回来的时候，记得pushup
    pushup(o);
}
LL query(int l, int r, int s = 1, int e = n, int o = 1)
{
    if(l <= s && e <= r)
    {
        //当前操作区间已经完全进入目标区间
        //到当前节点时，t[o]为正确的值
        return t[o];
    }
    //向下走之前，一定要pushdown
    pushdown(s, e, o);
    LL res = 0;
    int mid = (s + e) >> 1;
    //判断是否需要向左走，如果左儿子区间[s, mid]和[l, r]有交集，就要走
    if(mid >= l) res += query(l, r, s, mid, o << 1);
     //判断是否需要向右走，如果右儿子区间[mid+1,e]和[l, r]有交集，就要走
    if(mid + 1 <= r) res += query(l, r, mid + 1, e, o << 1 | 1); 
    //query没有进行修改，所以可以不pushup，当然写上也不影响
    pushup(o);
    return res;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
    }

    buildtree();

    while(q --)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int l, r;
            LL x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << query(l, r) << endl;
        }
    }
    return 0;
 }

异或线段树

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, M = N * 3; 
//t为线段树数组，lz为懒标记数组 
LL a[N], t[N << 2], lz[N << 2]; //开4倍空间，t[x]表示结点x所表示的区间的元素之和
//lz[o]表示：结点o还有lazy[o]这么大的一个数字，还没加给左右儿子
int n, q;
//异或线段树


void update(int s, int e, int o, LL x)
{
    if((e - s + 1) % 2)
    {
        t[o] ^= x;
    }
    lz[o] ^= x;
}

void pushup(int o)
{
    t[o] = t[o << 1] ^ t[o << 1 | 1];
}

void pushdown(int s, int e, int o)
{
    if(!lz[o]) return;

    int mid = (s + e) >> 1;

    update(s, mid, o << 1, lz[o]);
    update(mid + 1, e, o << 1 | 1, lz[o]);

    lz[o] = 0;

}

void add(int l, int r, LL x, int s = 1, int e = n, int o = 1)
{
    if(s >= l && e <= r)
    {
       update(s, e, o, x);
       return;  
    }

    pushdown(s, e, o);
    int mid = (s + e) >> 1;
    if(mid >= l) add(l, r, x, s, mid, o << 1);
    if(mid + 1 <= r) add(l, r, x, mid + 1, e, o << 1 | 1);
    pushup(o);

}
LL query(int l, int r, int s = 1, int e = n, int o = 1)
{
    if(s >= l && e <= r)
    {
       return t[o]; 
    }

    pushdown(s, e, o);
    LL res = 0;
    int mid = (s + e) >> 1;
    if(mid >= l) res ^= query(l, r, s, mid, o << 1);
    if(mid + 1 <= r) res ^= query(l, r, mid + 1, e, o << 1 | 1);
    pushup(o);
    return res;
}
void buildtree(int s = 1, int e = n, int o = 1)
{
    if(s == e)
    {
      t[o] = a[s];
      return;   
    }

    int mid = (s + e) >> 1;
    buildtree(s, mid, o << 1);
    buildtree(mid + 1, e, o << 1 | 1);
    pushup(o);
} 

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
    }

    buildtree();

    while(q --)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int l, r;
            LL x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << query(l, r) << endl;
        }
    }
    return 0;
 }

最值线段树

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10, M = N * 3; 
LL inf = 2e18;
//t为线段树数组，lz为懒标记数组 
LL a[N], tMax[N << 2], tMin[N << 2], lz[N << 2]; //开4倍空间，t[x]表示结点x所表示的区间的元素之和
//lz[o]表示：结点o还有lazy[o]这么大的一个数字，还没加给左右儿子
int n, q;
//最值线段树

//将区间[s, e]节点o加上x 
void update(int s, int e, int o, LL x)
{
   tMax[o] += x;
   tMin[o] += x;
   lz[o] += x;
}

void pushup(int o)
{
    tMax[o] = max(tMax[o << 1], tMax[o << 1 | 1]);
    tMin[o] = min(tMin[o << 1], tMin[o << 1 | 1]);
}

void pushdown(int s, int e, int o)
{
    if(!lz[o]) return;

    int mid = (s + e) >> 1;

    update(s, mid, o << 1, lz[o]);
    update(mid + 1, e, o << 1 | 1, lz[o]);

    lz[o] = 0;

}

void add(int l, int r, LL x, int s = 1, int e = n, int o = 1)
{
    if(s >= l && e <= r)
    {
       update(s, e, o, x);
       return;  
    }

    pushdown(s, e, o);
    int mid = (s + e) >> 1;
    if(mid >= l) add(l, r, x, s, mid, o << 1);
    if(mid + 1 <= r) add(l, r, x, mid + 1, e, o << 1 | 1);
    pushup(o);

}
LL queryMax(int l, int r, int s = 1, int e = n, int o = 1)
{
    if(s >= l && e <= r)
    {
       return tMax[o];  
    }

    pushdown(s, e, o);
    LL res = - inf;
    int mid = (s + e) >> 1;
    if(mid >= l) res = max(res, queryMax(l, r, s, mid, o << 1));
    if(mid + 1 <= r) res = max(res, queryMax(l, r, mid + 1, e, o << 1 | 1));
    return res;
}

LL queryMin(int l, int r, int s = 1, int e = n, int o = 1)
{
    if(s >= l && e <= r)
    {
       return tMin[o];  
    }

    pushdown(s, e, o);
    LL res = inf;
    int mid = (s + e) >> 1;
    if(mid >= l) res = min(res, queryMin(l, r, s, mid, o << 1));
    if(mid + 1 <= r) res = min(res, queryMin(l, r, mid + 1, e, o << 1 | 1));
    return res;
}
void buildtree(int s = 1, int e = n, int o = 1)
{
    if(s == e)
    {
      tMax[o] = tMin[o] = a[s];
      return;   
    }

    int mid = (s + e) >> 1;
    buildtree(s, mid, o << 1);
    buildtree(mid + 1, e, o << 1 | 1);
    pushup(o);
} 

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);  
    cin >> n >> q;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
    }

    buildtree();

    while(q --)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int l, r;
            LL x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << queryMax(l, r) << " " << queryMin(l, r) << endl;
        }
    }
    return 0;
 }

维护同时包含乘法，加法，复制操作的线段树
需要维护一种新运算：f = val * k + x
修改操作为乘法时候，即将x置为0，k为传入的参数
修改操作为加法时候， 将k置为1，x为传入的参数
修改操作为赋值时候， 将k置为0，x为传入的参数

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 9;
const ll p = 998244353;
int n, q;
ll t[N << 2], add[N << 2], mul[N << 2], a[N];

ll mo(ll x){return (x % p + p) % p;}

void update(int s, int e, int o, ll k, ll x)
{
    t[o] = mo( mo(t[o] * k) + mo(x * (e - s + 1)) );
    mul[o] = mo(mul[o] * k % p);
    add[o] = mo(mo(add[o] * k) + x);
}

void pushup(int o)
{
    t[o] = mo(t[o << 1] + t[o << 1 | 1]);
}

void pushdown(int s, int e, int o)
{
    int mid = (s + e) >> 1, ls = o << 1, rs = o << 1 | 1;

    update(s, mid, o << 1, mul[o], add[o]);
    update(mid + 1, e, o << 1 | 1, mul[o], add[o]);

    mul[o] = 1, add[o] = 0;
}

void buildTree(int s = 1, int e = n, int o = 1)
{
    mul[o] = 1;
    if(s == e)return t[o] = a[s], void();

    int mid = (s + e) >> 1;
    buildTree(s, mid, o << 1), buildTree(mid + 1, e, o << 1 | 1);
    pushup(o);
}

void modify(int l, int r, ll k, ll x, int s = 1, int e = n, int o = 1)
{
    //终端节点
    if(l <= s && e <= r)return update(s, e, o, k, x), void();

    pushdown(s, e, o);
    int mid = (s + e) >> 1;
    if(mid >= l)modify(l, r, k, x, s, mid, o << 1);
    if(mid + 1 <= r)modify(l, r, k, x, mid + 1, e, o << 1 | 1);
    pushup(o);
}

ll query(int l, int r, int s = 1, int e = n, int o = 1)
{
    //终端节点
    if(l <= s && e <= r)return t[o];

    pushdown(s, e, o);
    int mid = (s + e) >> 1;
    ll res = 0;
    if(mid >= l)res = mo(res + query(l, r, s, mid, o << 1));
    if(mid + 1 <= r)res = mo(res + query(l, r, mid + 1, e, o << 1 | 1));
    return res;
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    cin >> n >> q;
    for(int i = 1;i <= n; ++ i)cin >> a[i];
    buildTree();

    while(q --)
    {
        int op;cin >> op;
        if(op == 1)
        {
            ll l, r, x;cin >> l >> r >> x;
            modify(l, r, 1, x);
        }else if(op == 2)
        {
            ll l, r, x;cin >> l >> r >> x;
            modify(l, r, x, 0);
        }else if(op == 3)
        {
            ll l, r, x;cin >> l >> r >> x;
            modify(l, r, 0, x);
        }else if(op == 4)
        {
            ll l, r;cin >> l >> r;
            cout << query(l, r) << '\n';
        }
    }

    return 0;
}

康托展开
求解问题：康托展开属于组合数学中的一个知识点。用于求出一个排列在全排列中的排名。
详解参考链接： 康托展开详解

暴力代码 O(n^2)

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10, MOD = 998244353;

LL fac[N];
LL a[N];
void init()
{
    fac[0] = 1;
    for(int i = 1; i < N; i ++)
     {
        fac[i] = (fac[i - 1] * i) % MOD;
     }
}
int n;
LL cantor(LL a[])
{
    LL res = 0;

    for(int i = 1; i <= n; i ++)
    {
        int s = 0;
        for(int j = i; j <= n; j ++)
        {
            if(a[j] < a[i]) s ++;
        }

        res = (res + (fac[n - i] * s) % MOD) % MOD;
    }
    return res + 1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    init();
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    cout << cantor(a) << endl;  

    return 0;

}

树状数组优化代码 O(nlogn)

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10, MOD = 998244353;

LL fac[N];
LL a[N];
LL t[N];
int n;
int lowbit(int x)
{
    return x & -x;
}

void add(int x, LL w)
{
    for(int i = x; i <= n; i += lowbit(i)) t[i] += w;
}

LL query(int x)
{
    LL s = 0;
    for(int i = x; i > 0; i -= lowbit(i))
    s += t[i];

    return s; 
}
void init()
{
    fac[0] = 1;
    for(int i = 1; i < N; i ++)
     {
        fac[i] = (fac[i - 1] * i) % MOD;
     }
}

LL cantor(LL a[])
{
    LL res = 0;

    for(int i = 1; i <= n; i ++)
    {
        LL s = 0;
        s = query(a[i]) - 1;
        add(a[i], -1);
        res = (res + (fac[n - i] * s) % MOD) % MOD;
    }
    return res + 1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    init();
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    for(int i = 1; i <= n; i ++) add(i, 1);

    cout << cantor(a) << endl;  

    return 0;

}