链表专题
转发的朋友请带上原博地址: 我的博客
首先我们都知道,链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。
一般用结构体来表示。
struct ListNode {
int val;
struct ListNode *next;
};
其中 $val$ 是存储这个节点的值, $*next$ 是存储下一个节点的位置。这样每一个节点都知道下一个节点的位置,就可以以非连续、非顺序的存储结构,把一段数据连续起来。
链表本身是个不难理解的东西,重要的是学会如何在问题中使用它。
例题
于是我们接下来就在实战中学习。
注:下面的例题讲解是学习完 Week2 链表专题 - bilibili 后的产物,若是对本博客不感兴趣的可以直接去看原视频。
- LeetCode 19. 删除链表的倒数第N个节点
- LeetCode 237. 删除链表中的节点
- LeetCode 83. 删除排序链表中的重复元素
- LeetCode 61. 旋转链表
- LeetCode 24. 两两交换链表中的节点
- LeetCode 206. 反转链表
- LeetCode 92. 反转链表 II
- LeetCode 160. 相交链表
- LeetCode 142. 环形链表 II
- LeetCode148. 排序链表
No.1 LeetCode 19. 删除链表的倒数第N个节点
原题地址:LeetCode 19. 删除链表的倒数第N个节点
题目描述
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
- 给定的 n 保证是有效的。
进阶:
- 你能尝试使用一趟扫描实现吗?
解题思路:
由于题目中使用的是单向链表,只能从头开始走到尾,而不能逆着走。
看到这道题的时候,我第一想法是,先把链表跑一遍,这时我们可以知道它的长度 $m$。
再然后,计算得出倒数的第 $n$ 个节点是正数的第 $m - n + 1$ 个,这个时候我们再跑一遍就可以知道我们要删除的是哪一个节点了。
但题目的进阶要求我们只能使用一趟扫描来实现,上面的想法自然是不满足题目要求的。
由于我们的头结点 $head$ 也有可能被删除,于是我们要创建一个虚拟头结点 $dummy$ ,让 $dummy -> next = head;$
再然后,我们要用两个指针,$first = dummy, second = dummy$
这两个指针有什么用呢,我们首先让 $first$ 指针比 $second$ 指针先移动 $n$ 次。
这时 $first$ 指针已经指到了第 $n$ 个结点,而 $second$ 指针依然指着虚拟结点 $dummy$ 也就是第0个结点。
等到 $first$ 指针比 $second$ 指针先移动 $n$ 次后,我们的 $second$ 指针就可以开始和 $first$ 指针一起开始移动了。
这样当 $first$ 指针指到末尾的时候, $second$ 刚好到倒数第 $n - 1$ 个结点。
而这个结点的 $next$ 就是我们要删除的结点。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
auto dummy = new ListNode(-1);
dummy -> next = head;
auto first = dummy, second = dummy;
while(n--)
first = first -> next;
while(first -> next){
first = first -> next;
second = second -> next;
}
second -> next = second -> next -> next;
return dummy -> next;
}
};
No.2 LeetCode 237. 删除链表中的节点
原题地址: LeetCode 237. 删除链表中的节点
题目描述
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点,你将只被给定要求被删除的节点。
现有一个链表 – head = [4,5,1,9],它可以表示为:

示例1:
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
示例2:
输入: head = [4,5,1,9], node = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.
说明:
- 链表至少包含两个节点。
- 链表中所有节点的值都是唯一的。
- 给定的节点为非末尾节点并且一定是链表中的一个有效节点。
- 不要从你的函数中返回任何结果。
解题思路:
这道题呢,怎么说呢,就是一个很简单的链表删除元素操作。
但有所不同的是,你并不知道该删除的点的上一个结点的位置。
所以你不能直接简单的将要删除的结点的上一个结点的 $next$ 直接改成要删除的结点的 $next$,因为你无从得知要删除的结点的上一个结点在哪。
既然不能直接来删除,那就只能曲线救国了。
假设我们 $A[a] \rightarrow B[b] \rightarrow C[c]$ 中要删除 $B$ ,但是我们不能让 $A[a] \rightarrow C[c]$。
那么,我们可以将 $B$ 结点的 $val$ 值改成 $C$ 结点的 $val$ 值 ,于是就变成了 $A[a] \rightarrow B[c] \rightarrow C[c]$。
最后我们再将 $C$ 删除就可以了,最后就是$A[a] \rightarrow B[c]$ 这样虽然没能直接删除 $B[b]$ ,但是在我们查看链表的时候 $b$ 已经被我们删除了,而其他数据并没有改变。
所以我们曲线救国成功。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void deleteNode(ListNode* node) {
node -> val = node -> next -> val;
node -> next = node -> next -> next;
// *node = *(node -> next); 上面两行代码,可以简写成这一行代码。
}
};
No.3 LeetCode 83. 删除排序链表中的重复元素
原题链接: LeetCode 83. 删除排序链表中的重复元素
题目描述
给定一个排序链表,删除所有重复的元素,使得每个元素只出现一次。
示例1:
输入: 1->1->2
输出: 1->2
示例2:
输入: 1->1->2->3->3
输出: 1->2->3
解题思路:
这道题也不难,题目本身是排好序的,所以重复的数字一定是紧挨在一起的。
因此我们只需要从头结点开始走,每次判断该结点和下一个结点的 $val$ 是否相等,若相等则删除下一个结点。
这里需要注意的是,由于可能不止有一个数与该结点重复,所以删除了第一个重复的数字的结点后,还得继续判断新的结点是否相等。
只有当该结点与下一结点不相等的时候,猜移动到下一个结点的位置进行判断。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
auto p = head;
while(p){
if(p -> next && p -> val == p -> next -> val)
p -> next = p -> next -> next;
else
p = p -> next;
}
return head;
}
};
No.4 LeetCode 61. 旋转链表
原题链接: LeetCode 61. 旋转链表
题目描述
给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例2:
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NUL
解题思路:
分析题目我们可以发现,虽然题目给的示例是一次一次的移动。
但其实我们可以一次性移动完毕,因为我们发现如果是将链表每个节点向右移动 k 个位置,那么就是将最后一个的结点的 $next$ 变成 $head$ 头结点, 然后倒数第 $k$ 个点就是新的头结点。
因此我们可以像例题一一样,用两个指针找到倒数第 $K - 1$ 个点的位置,然后将 $k-1$ 结点的 $next$ 设置为 $NULL$ 。最后将将最后一个的结点的 $next$ 变成 $head$ 头结点就行了。
但之后我发现,它的 $K$有可能会大于链表的长度,所以要先计算出链表的长度 $n$, 然后 $k$ %$= n; $ $k$ 就是小于等于链表长度的了。
注意要记得判断空链表的情况,这个时候可以直接返回 $NULL$.
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if(!head)
return NULL;
int n = 0;
for(auto p = head; p; p = p->next)
n++;
k %= n;
auto first = head, second = head;
while(k--)
second = second -> next;
while(second -> next){
first = first -> next;
second = second -> next;
}
second -> next = head;
head = first -> next;
first -> next = NULL;
return head;
}
};
No.5 LeetCode 24. 两两交换链表中的节点
原题链接: LeetCode 24. 两两交换链表中的节点
题目描述
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例:
给定 1->2->3->4, 你应该返回 2->1->4->3.
解题思路:
这道题的难点在于怎么将 $A \rightarrow B$ 变成 $A \leftarrow B$ .
其实这个问题也不难解决,只要提前把 $A$、$B$ 以及 $B$ 的下一个结点 $C$ 存储下来,然后就将各个结点的 $next$ 更新成交换后的结点就行,然后再后移进行新的交换即可。
交换过程如图所示:
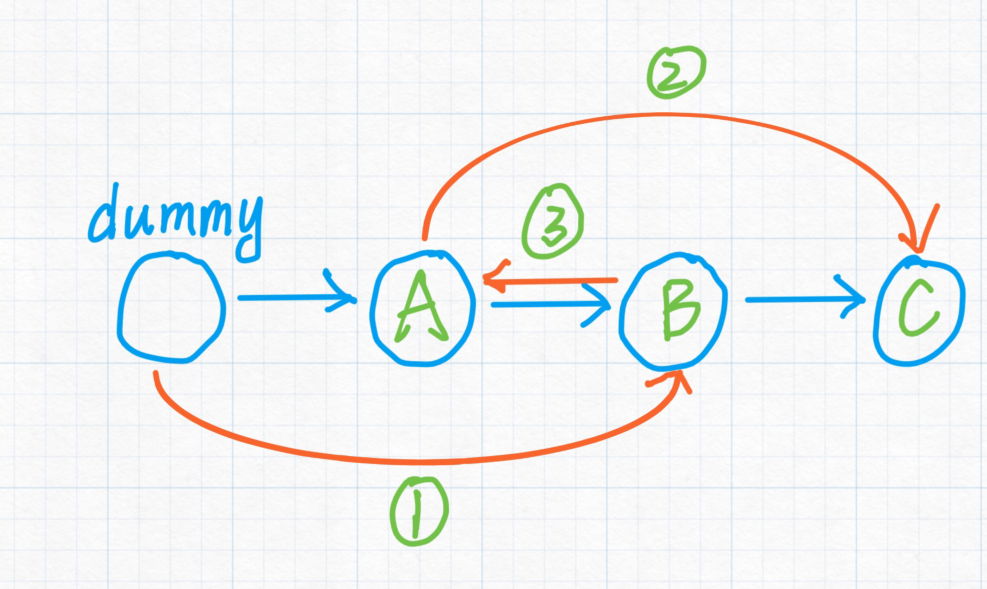
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
auto dummy = new ListNode(-1);
dummy -> next = head;
for(auto p = dummy; p->next && p->next->next; p = p->next->next){
auto a = p->next, b = a -> next;
p->next = b;
a->next = b->next;
b->next = a;
}
return dummy->next;
}
};
No.6 LeetCode 206. 反转链表
原题链接:LeetCode 206. 反转链表
题目描述
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
解题思路:
这道题和上一道题很类似,只不过他是每一个数之间都反转。
所以交换方式和上一道题一样,但是移动方式就有一点区别了, 即 $a= b, b = c;$ 这样右移动一位即可,而不是像上一题移动两位。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head)
return NULL;
auto a = head, b = head->next;
while(b){
auto c = b->next;
b->next = a;
a= b, b = c;
}
head->next = NULL;
return a;
}
};
No.7 LeetCode 92. 反转链表 II
原题链接:LeetCode 92. 反转链表 II
题目描述
反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。
说明
1 ≤ m ≤ n ≤ 链表长度。
示例:
输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL
解题思路:
这道题先找到要反转范围的结点的位置后, 按照上一题的反转方法进行反转即可。
若是 $m == n$, 可以直接返回该链表就行。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int m, int n) {
if(m == n)
return head;
auto dummy = new ListNode(-1);
dummy->next = head;
auto a = dummy, d = dummy;
for(int i = 1; i < m; i++)
a = a->next;
for(int i = 0; i < n; i++)
d = d->next;
auto b = a->next, c = d->next;
for(auto p = b, q = b->next; q != c;){
auto o = q->next;
q->next = p;
p = q, q = o;
}
b->next = c;
a->next = d;
return dummy->next;
}
};
No.8 LeetCode 160. 相交链表
原题链接:LeetCode 160. 相交链表
题目描述
写一个程序,找到两个单链表相交的起始节点。如下面的两个链表:
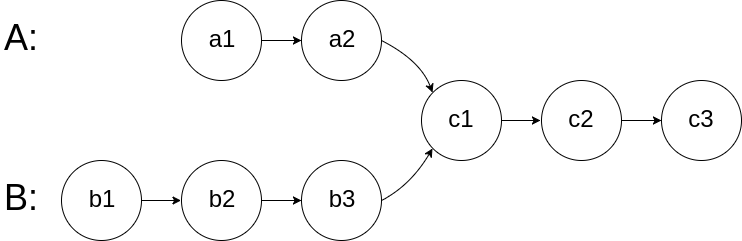
在节点 c1 开始相交。
示例1:
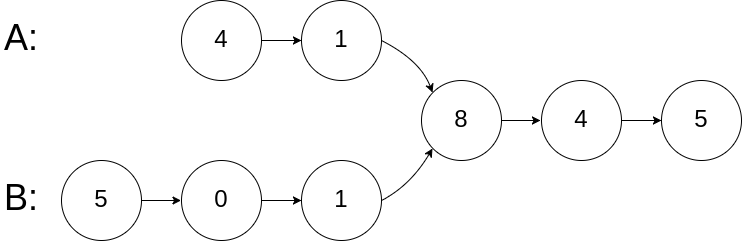
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例2:
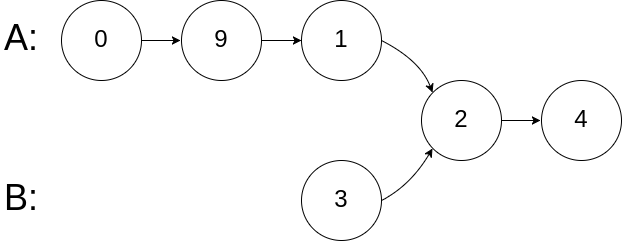
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例3:
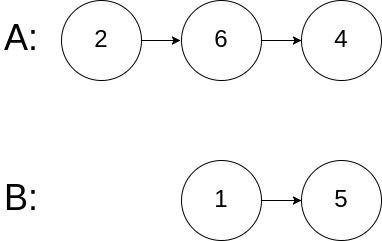
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
- 如果两个链表没有交点,返回 null.
- 在返回结果后,两个链表仍须保持原有的结构。
- 可假定整个链表结构中没有循环。
- 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
解题思路:
分别用两个指针 $a,b$ 从两个头结点 $A,B$ 开始移动,假设 $a$ 先到链表末尾,那么就将 $a$ 变到链表 $B$ 的头结点的位置, 然后 $a,b$ 继续移动。
等到 $b$ 到链表末尾后,就将 $b$ 变到链表 $A$ 的头结点的位置,当他们相遇时,相遇的点就是相交的点。
为什么呢?
假设 $A$ 链条私有部分长度为 $x$,$B$ 链条私有部分长度为 $y$ 、$A,B$ 链条公有部分长度为 $z$。当他们相遇时,$A$ 走了 $x+z+y$ 、$B$ 走了 $y+z+x$, 也就是两个链表的相交点。
如果是示例3 的情况,他们会在都等于 $NULL$ 的时候相遇,因此返回的值也是符号题目要求的。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
auto a = headA, b = headB;
while(a != b){
if(a)
a = a->next;
else
a = headB;
if(b)
b = b->next;
else
b = headA;
}
return b;
}
};
No.9 LeetCode 142. 环形链表 II
原题链接: LeetCode 142. 环形链表 II
题目描述
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例1:
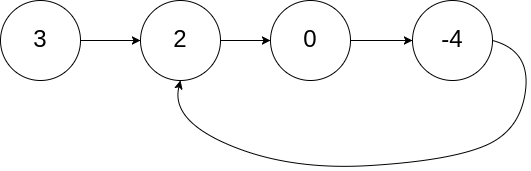
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
示例2:
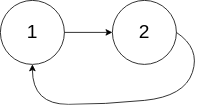
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。

解题思路:
这道题是用的快慢指针来,首先建立两个指针 $a, b$ ,两个都最初指向头结点 $head$ ,但是 $a$ 每次移动一步、 $b$ 每次移动两步。
当两个指针第一次相遇后, 将 $a$ 移动到头结点 $head$ ,然后 $a,b$ 再都以每次一步的速度同时移动,等他们再次相遇的时候的节点位置,就是我们环开始的位置。
至于是为什么呢…我最开始看到这个算法的时候很懵逼…然后证明了一下,才明白这是为什么…
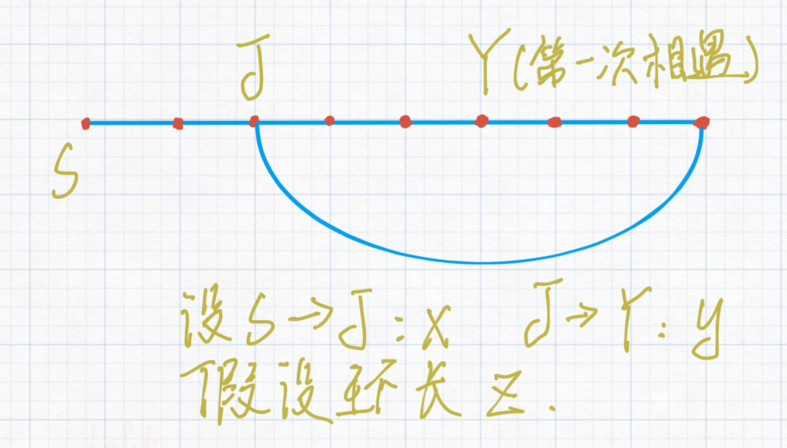
首先先如图假设一下。
当 $a$ 、$b$ 第一次相遇的时候:$a$ 走了 $x +y + nz$ ($n = 0,1,2…$)、$b$ 走了 $2x +2y + 2nz$ ($n = 0,1,2…$)
然后将 $a$ 移动到头结点、当 $a$ 、$b$ 再一次相遇的时候:$a$ 走了 $2x +y + nz$ ($n = 0,1,2…$)、$b$ 走了 $3x +2y + 2nz$ ($n = 0,1,2…$)
它们相差的步数是 $x +y + nz$ 可得 $x + y == mz$($m = 0,1,2…$) ,所以在第一次相遇后再走 $x$ 步就一定可以到达 $J$ 点。
而刚好 $a$ 从结头到 $J$ 点的距离刚好为 $x$。
所以他们第二次相遇的时候,就是我们要的结果
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
auto a = head, b = head;
while(b){
a = a->next;
b = b->next;
if(b)
b = b->next;
else break;
if(a == b){
a = head;
while(a != b ){
a = a->next;
b = b->next;
}
return a;
}
}
return NULL;
}
};
No.10 LeetCode148. 排序链表
原题链接: LeetCode148. 排序链表
题目描述
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例1:
输入: 4->2->1->3
输出: 1->2->3->4
示例2:
输入:-1->5->3->4->0
输出: -1->0->3->4->5
解题思路:
这道题要用到之前用的反转链表,然后再选择一种满足题目要求的算法即可。
而满足这道题的排序算法是归并排序。
那什么是归并排序呢?
归并排序就是,当我有一个如图的数组,他的左边部分和右边部分都是排好了的。

然后我们将他拆分成两个数组,并准备一个新的空数组来放他们。
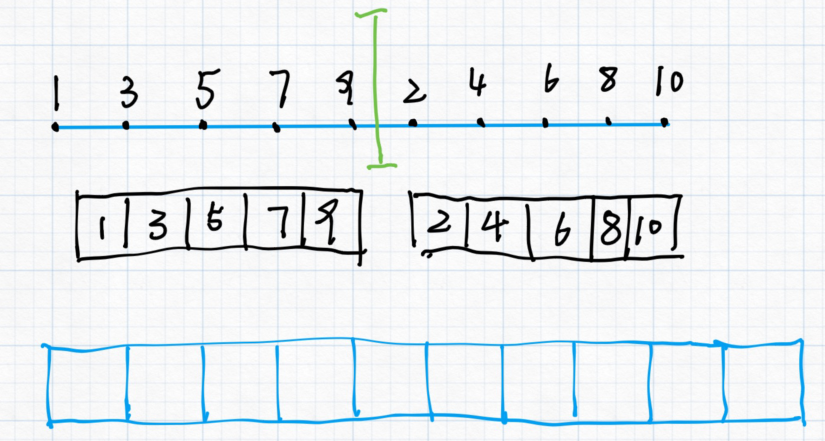
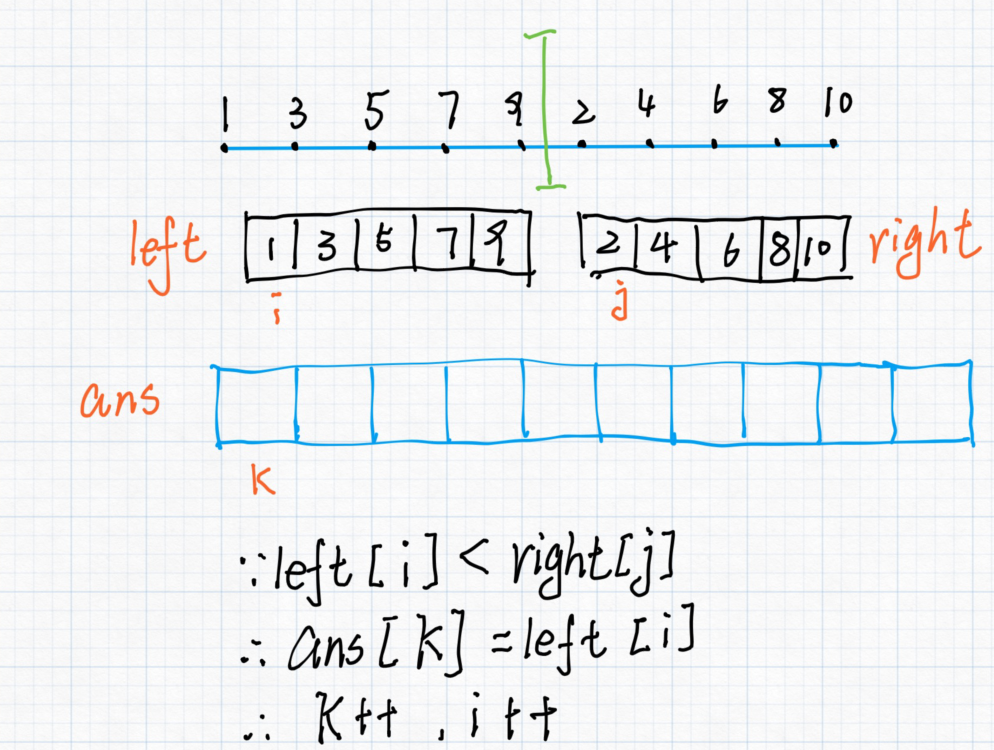
然后 $i$ 指向 $left$ 数组的第一个, $j$ 指向 $right$ 数组的第一个, $k$ 指向 $ans$ 数组的第一个。
然后判断 $left[i] < right[j]$ 若 $left[i]$ 小一些,则将 $left[i]$ 放到 $ans[k]$ 里面。
若 $right[j]$ 小一些,则将 $right[j]$ 放到 $ans[k]$ 里面,
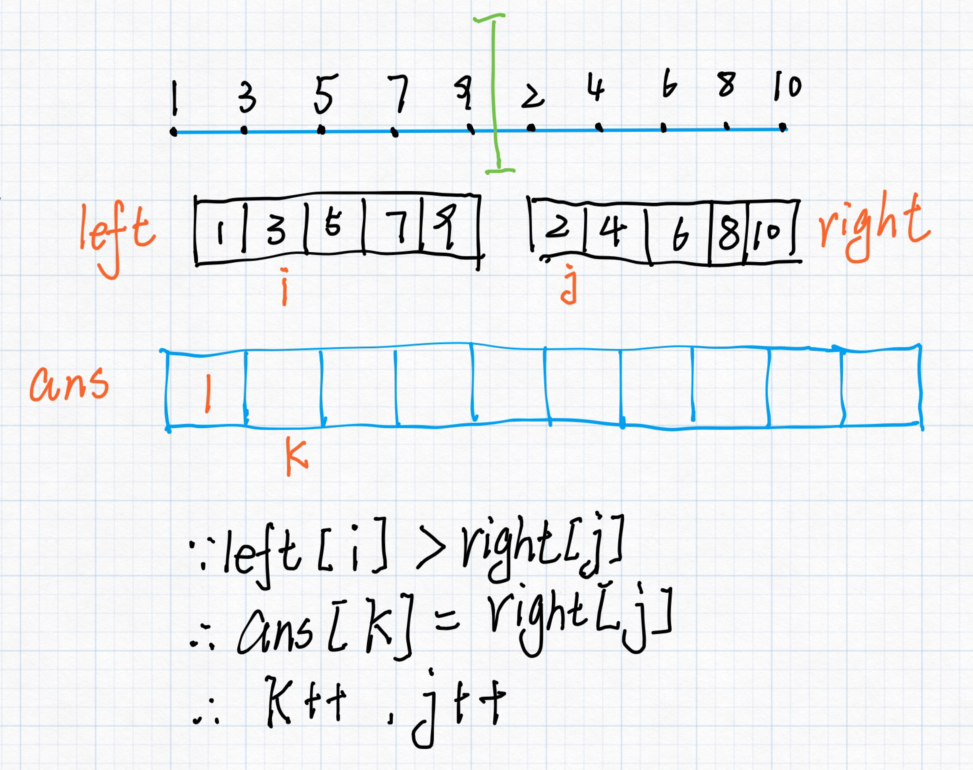
直到数组里面的的数字都放完为止。
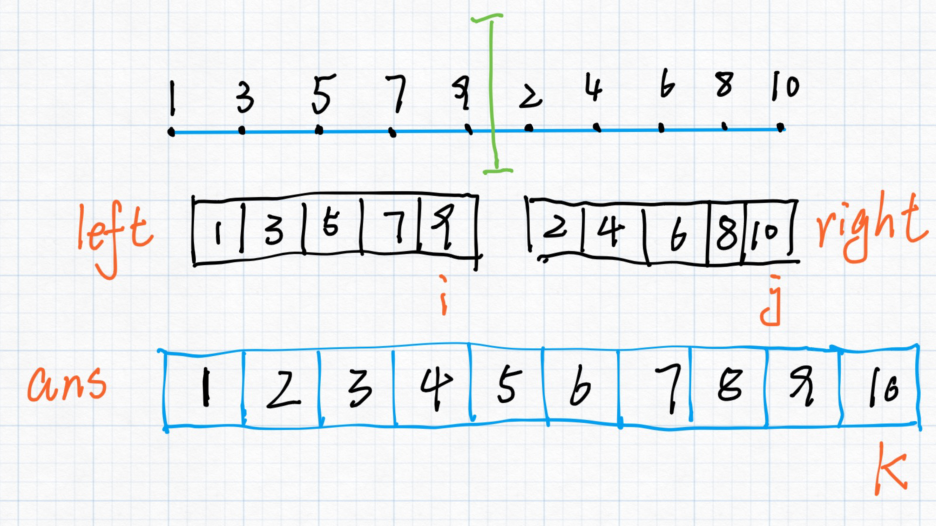
而这道题就是采用的归并排序,先将 $n$ 个结点分成 $i$ 个数组 ($i$ 从1开始增大,直到将整个链表一分为二),然后每次两个数组进行归并排序,最后把整个串起来就可以了。
$AC$代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
int n = 0;
for (ListNode *p = head; p; p = p->next) n ++ ;
ListNode *dummy = new ListNode(-1);
dummy->next = head;
for (int i = 1; i < n; i *= 2)
{
ListNode *begin = dummy;
for (int j = 0; j + i < n; j += i * 2)
{
ListNode *first = begin->next, *second = first;
for (int k = 0; k < i; k ++ )
second = second->next;
int f = 0, s = 0;
while (f < i && s < i && second)
if (first->val < second->val)
{
begin = begin->next = first;
first = first->next;
f ++ ;
}
else
{
begin = begin->next = second;
second = second->next;
s ++ ;
}
while (f < i)
{
begin = begin->next = first;
first = first->next;
f ++ ;
}
while (s < i && second)
{
begin = begin->next = second;
second = second->next;
s ++ ;
}
begin->next = second;
}
}
return dummy->next;
}
};
小结
这次是链表专题,整个学习的过程中感觉难点就是有点抽象。
所以学这一段的时候我就是在不断画图…
不过学到最后感觉也就那个样吧,哈哈。


# 6b
“这样当
first指针指到末尾的时候,second刚好到倒数第n−1个结点。”应该是倒数第
n + 1个吧? 然后second 的next指向倒数第n - 1,这样就删除了倒数第N个?非常详细,很棒啊!
谢谢 :)