数字三角形模型
数字三角形
数字三角形
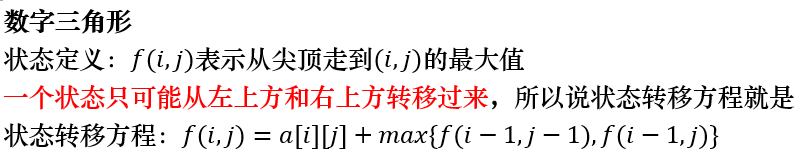
容易发现,如果我们将金字塔的每个点抽象成图上的点,如果点$A$能从$B$转移,那么从$B$到$A$连一条有向边。于是整张状态空间构成的图为。
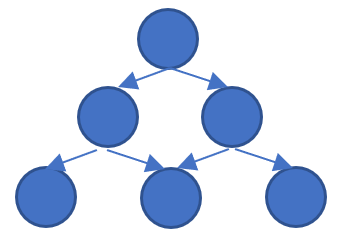
可以发现,我们要求这张图的拓扑序,就是金字塔层序遍历,于是不难写出代码。
#include <iostream>
#include <cstdio>
using namespace std;
const int N=1e3+5;
int n,ans;
int a[N][N],f[N][N];
int main() {
cin>>n;
for(int i=1;i<=n;i++) //二维数组存储金字塔
for(int j=1;j<=i;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++) //层序遍历
for(int j=1;j<=i;j++)
f[i][j]=a[i][j]+max(f[i-1][j],f[i-1][j-1]);
for(int i=1;i<=n;i++) //最后需要遍历底下所有点
ans=max(ans,f[n][i]);
cout<<ans;
return 0;
}
摘花生
摘花生
与上一题几乎相同
#include <bits/stdc++.h>
using namespace std;
const int N=1e2+5;
int T,n,m,a[N][N],f[N][N];
int main() {
cin>>T;
while(T--) { //T组数据
memset(f,0,sizeof(f)); //每组数据开始前先请空,不过这题不清也没关系
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++) //状态转移
for(int j=1;j<=m;j++)
f[i][j]=a[i][j]+max(f[i-1][j],f[i][j-1]);
cout<<f[n][m]<<endl;
}
return 0;
}
子序列模型
最长不下降子序列
#include <iostream>
#include <cstdio>
using namespace std;
const int N=200+5;
int b[N],f[N],n,ans;
int pre[N],path[N];
void dfs(int idx) { //递归调用
if(idx==0)
return ;
dfs(pre[idx]); //递归前面的
cout<<b[idx]<<' ';
}
int main() {
cin>>n;
for(int i=1;i<=n;i++) {
cin>>b[i];
f[i]=1; //初值
}
for(int i=1;i<=n;i++)
for(int j=1;j<i;j++)
if(b[j]<=b[i]) //如果这个点能够跟他构成序列
if(f[j]+1>=f[i]) { //并且f值+1大于它的f
f[i]=f[j]+1; //更新f值
pre[i]=j; //更新pre值
}
for(int i=1;i<=n;i++)
if(f[ans]<f[i])
ans=i; //记录最长不下降子序列的末尾
cout<<"max="<<f[ans]<<endl;
dfs(ans); //输出方案
return 0;
}
怪盗基德的滑翔翼
怪盗基德的滑翔翼
题目其实很简单,只需要正着求一遍最长下降子序列,然后反着求一边最长下降子序列,取两遍的最大值即可
#include <bits/stdc++.h>
using namespace std;
const int N=1e2+5;
int T,n,a[N],f[N],ans;
int main() {
cin>>T;
while(T--) {
ans=0;
cin>>n;
for(int i=1;i<=n;i++) {
cin>>a[i];
f[i]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=i-1;j++)
if(a[i]<a[j]) //最长下降子序列
f[i]=max(f[i],f[j]+1);
for(int i=1;i<=n;i++) {
ans=max(ans,f[i]); //取出长度
f[i]=1; //重新赋值
}
for(int i=1;i<=n/2;i++)
swap(a[i],a[n-i+1]); //序列翻转
for(int i=1;i<=n;i++)
for(int j=1;j<=i-1;j++)
if(a[i]<a[j])
f[i]=max(f[i],f[j]+1);
for(int i=1;i<=n;i++)
ans=max(ans,f[i]);
cout<<ans<<endl;
}
return 0;
}
最长公共子序列
#include <bits/stdc++.h>
using namespace std;
const int N=1000+5;
char a[N],b[N];
int f[N][N],ans;
int main() {
scanf("%s%s",a+1,b+1);
for(int i=1;a[i];i++) //a[i]如果!=0,那么就是没有遍历完,是一个常用的技巧,也可以用strlen函数
for(int j=1;b[j];j++) {
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j]) //状态转移
f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
cout<<f[strlen(a+1)][strlen(b+1)];
return 0;
}


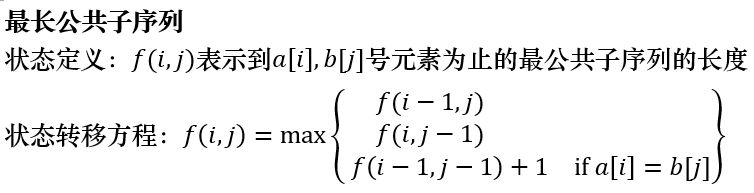

orz
%%%