算法笔记会持续更新

还有诸多代办，不过不用着急，作者还有很长的花期，半年内还会学很多算法嘟，一定会完成的^ _ ^😋😋

前言：总结来自学习经历中的所有内容，主要是板子以及思路整理，分块内容部分有详解传送门，题目传送门主要是本人学该算法时的题目来源（所以就算传送门不能使用的话，可以上洛谷上面搜题啦，上面的题目尊嘟很多~~）

基础算法：

排序算法

统一以升序为列

冒泡排序

思路： 相邻数如果左边的比右边的大，交换两个相邻数

void effervescence_sort(int q[] , int n){
    for(int i = 0; i < n; i++) {
        for(int j = n - 1; j >= i; j--) {
            if(q[j] < q[j - 1]) swap(q[j], q[j - 1]);
        }
    }
}

选择排序

思路： 每次（第i次）访问找到当前最小值，放在第i个位置，执行n次

void select(int q[], int n){
    for(int i = 0; i < n; i++) {
        int mi = q[i]; 
        int idx = i;
        for(int j = i; j < n; j++) {
            if(mi > q[j]) {
                mi = q[j];
                idx = j;
            }
        }
        swap(q[i], q[idx]);
    }
}

快速排序

思路： 先选定一个区间内的随机值（本做法选最左端），用其作为标准，然后遍历区间一个指针在最左端，一个在最右端，往中间靠拢，大于标准的放在右边，小于标准的放在左边，然后重复递归左右区间

void quick_sort(int q[], int l, int r){
    if(l >= r) return ;
    int x = q[l], i = l - 1, j = r + 1;
    while(i < j) {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

归并排序

思路：把数组从中间拆开，继续递归左右两个数组，每次排序当前数组之前，拆分的左右区间都已经排好序，通过双指针排当前数组，直到完成排序

int q[N], tmp[N]; // q原数组， tmp辅助数组

void merge_sort(int q[], int l, int r){
    if(l >= r) return ;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r) {
        if(q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }

    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];
    for(i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}

传送门

785. 快速排序 - AcWing题库

二分，三分

二分

思路： 对升序的数组而言，直接找中间值就可以进行折中判断，最多次数为log(n)次

整形二分

又分为左查找和右查找，以应付数组中有多个该值

int find_left(int x) { // 左查找
    int l = 0, r = n - 1;
    while(l < r) {
        int mid = l + r >> 1;
        if(a[mid] >= x) r = mid;
        else l = mid + 1;
    }
    if(a[l] == x) return l;
    return -1;
}

int find_right(int x) { // 右查找
    int l = 0, r = n - 1;
    while(l < r) {
        int mid = l + r + 1 >> 1;
        if(a[mid] <= x) l = mid;
        else r = mid - 1;
    }
    if(a[l] == x) return l;
    return -1;
}

浮点二分

浮点直接查找即可

// 求它的三次方根
double find(double x) {
    double l = 0, r = 1e18;
    while(r - l > 1e-18) {
        double mid = (l + r) / 2;
        if(mid * mid * mid > x) r = mid;
        else l = mid;
    }
    return l;
}

浮点二分可以说是整形二分的简化版

传送门

整形：789. 数的范围 - AcWing题库

浮点：790. 数的三次方根 - AcWing题库

三分

while(r - l > eps) {
        double k = (r - l) / 3.0;
        double mid1 = l + k, mid2 = r - k;
        if(f(mid1) > f(mid2)) r = mid2;
        else l = mid1;
    }

前缀和，差分

他们两的关系太好了所以放一起

前缀和

可以快速查询区间和

思路：把数组依次累加，a为原数组，s为前缀和数组

构造

一维前缀和

构造：

for(int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];

查询：

cout << s[i] - s[j];

二维前缀和

构造：

for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            s[i][j] = s[i - 1][j] + s[i][j - 1] -s[i - 1][j - 1] + a[i][j];

查询：

cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] +s[x1 - 1][y1 - 1] << endl;

双指针

思路： 遍历数组时，一个指针移动，另外一个指针保持不动，直到满足要求停止前一个指针移动

找a,b中相同的元素

int sum = 0, j = 0;
for(int i = 0; i < n; i++) {
    while(j < m && b[j] < a[i]) j++;
    if(b[j] == a[i]) sum++;
}

找数组元素的目标和

for(int i = 0, j = m - 1; i < n; i ++ ){
    while(j >= 0 && a[i] + b[j] > x) j --;
    if(a[i] + b[j] == x) cout << i << " " << j << endl;
}

传送门

799. 最长连续不重复子序列 - AcWing题库

799. 最长连续不重复子序列 - AcWing题库

离散化

思路： 一个数组的值过大，但是我们只需要用到其中间的大小关系的时候，我们就需要用到离散化，将其大小关系保留，映射到1~n

void work(int a[]) { 
    for(int i = 0; i < n; i ++ ) p[i] = i;
    sort(p, p + n, [&](int x, int y) { 
        return a[x] < a[y];
    });
    for(int i = 0; i < n; i ++ ) a[p[i]] = i; 
}

传送门

505. 火柴排队 - AcWing题库

位运算

将一个数以二进制表示，就能够通过0，1来解决很多事情

思路： 通过&，^，|等二进制常用符号实现位运算

求一个数变为2进制后1的个数

int lowbit(int x) {
    return x & -x;
}

int main() {
    int res = 0;
    int x; cin >> x;
    while(x) x -= lowbit(x) , res ++;
}

传送门

801. 二进制中1的个数 - AcWing题库

高精度

高精度加法

思路：通过动态数组，将个位数放在数组的第一个位置，往后处理，每位要同时加上进位t / = 10

vector<int> add(vector<int> &A, vector<int> &B) {
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size() || i < B.size(); i++) {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if(t) C.push_back(1);
    return C;
}

高精度减法

思路：判断两个数的大小，减数小则为正，否则为负，同时判断是否需要借位和有无被借位，处理完后判断有无前导零

bool cmp(vector<int> &a, vector<int> &b){ 
    if(a.size() != b.size()) return a.size() > b.size();
    for(int i = a.size() - 1; i >= 0; i -- ){
        if(a[i] != b[i]) return a[i] > b[i];
    }
    return true;
}

vector<int> sub(vector<int> &a, vector<int> &b){
    vector<int> c;
    int t = 0;
    for(int i = 0; i < a.size(); i ++ ){
        t = a[i] - t;
        if(i < b.size()) t -= b[i];
        c.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    while(c.size() > 1 && c.back() == 0) c.pop_back();

    return c;
}

高精度乘法

思路： 优先考虑乘法的效果，个位乘十位，答案会在十位上，百位成百位，答案会在万位上，那么处理每一位，最后在处理进位即可

 vector<int> mul(vector<int> &A, vector<int> &B) {
    vector<int> C(A.size() + B.size() + 5, 0); 
    for (int i = 0; i < A.size(); i++)
        for (int j = 0; j < B.size(); j++)
            C[i + j] += A[i] * B[j];
    int t = 0;
    for (int i = 0; i < C.size(); i++) { 
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back(); 
    return C;
}

高精度除法

思路： 优先考虑乘法的效果，个位乘十位，答案会在十位上，百位成百位，答案会在万位上，那么处理每一位，最后在处理进位即可

bool cmp(vector<int> &A, vector<int> &B){
    if(A.size() != B.size()) return A.size() > B.size();
    for(int i = A.size() - 1; i >= 0; i--){
        if(A[i] != B[i]) return A[i] > B[i]; 
    }
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B){
    vector<int> C;
    int t = 0;
    for(int i = 0;i < A.size() || t; i++){
        t = A[i] - t;
        if(i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    while(C.size() > 1 && C.back()==0) C.pop_back();
    return C;
}

vector<int> div(vector<int> &A, vector<int> &B, vector<int> &r){
    vector<int> C;
    if(!cmp(A, B)){
        C.push_back(0);
        r = A;
        return C;
    }
    int j = B.size();
    r.assign(A.end() - j, A.end());
    while(j <= A.size()){
        int k = 0;
        while(cmp(r, B)){
            vector<int> s = sub(r, B);
            r.clear();
            r.assign(s.begin(), s.end());
            k++;
        }
        C.push_back(k);
        if(j < A.size()) r.insert(r.begin(), A[A.size() - j - 1]);
        if(r.size() > 1 && r.back() == 0) r.pop_back();
        j++;
    }
    reverse(C.begin(),C.end());
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

注（出处）：AcWing 794. 高精度除法 （A/B） C++实现 - AcWing

传送门

791. 高精度加法 - AcWing题库

792. 高精度减法 - AcWing题库

793. 高精度乘法 - AcWing题库

794. 高精度除法 - AcWing题库

STL：

List

定义：

list<int> node;

常用函数：

node.push_back();  // 插入

list<int>::iterator it = node.begin();
for(it; it != node.end(); it++) // 遍历
    cout << *it << " "; // 输出

node.erase(it); // 删除该位置

Queue

定义方式：

queue <Type, Container> 名称;

创建队列 ：

queue <int> q;
queue <char> q;
queue<string> q;

常用函数

q.push() // 队尾插入元素
q.pop() // 删除队头元素
q.size() // 返回元素个数
q.empty() // 空队列返回true
q.front() // 返回队列第一个元素
q.back() // 发挥队列最后一个元素

Stack

定义方式：

stack<Type> st; 

常用函数：

st.push(item); // 插入
st.top(); // 访问栈顶
st.pop(); // 弹出栈顶
s.size(); // 栈大小
s.empty(); // 是否为空

Map：

定义方式：

map<Type1, Type2> 名称;

创建map：

map<int, int> mp;
map<string, int> mp;
map<pair<int,int>, int> mp;

常用函数：

mp.insert(); // 向map内插入一个元素
mp.find(); // 查找一个元素， 返回值是key
mp.clear(); // 清空map
mp.erase(); // 删除一个元素
mp.size(); // 返回map的个数

Set:

定义方式：

set <Type> 名称;

创建set:

set <int> se;
set <string> se;

常用函数：

se.begin(); // 返回set的第一个元素
se.end(); // 返回set的最后一个元素
se.clear(); // 清空set
se.empty(); // 若set不含元素，返回true
se.max_size(); // 返回set可能包含的元素的最大个数
se.size(); // 返回当前set的元素个数

Vector：

定义方式：

vector<Type> 名称; // 一维
vector<vector<Type>> 名称 // 二维

二维初始化

a.resize(n + 1, vector<char>(m + 1));
st.resize(n + 1, vector<bool>(m + 1, false));

常用函数：

可以当成数组直接使用，有些函数故此不描述

a.size(); // 大小
a.clear(); // 清空
sort(a.begin(), a.end()); // 排序

Priority_queue

定义方式：

priority_queue<Type, Container, Functional> 名称;

换而言之，先申明类型，选择存储容器类型，最后是一个表示升降的函数

创建优先队列 ：(大根堆)

priority_queue <int> q;  // 不写默认大根堆
priority_queue <int, vector<int>, less<int>> q;

创建优先队列 ：(小根堆)

priority_queue<int, vector<int>, greater<int>> q;

创建优先队列时，如果int写的是pair<int, int>，先比较第一个，第一个相等的情况下比较第二个

常用函数 ：

q.top(); // 访问队头元素
q.empty(); // 队列是否为空
q.size(); // 返回队列内元素个数
q.push(); // 插入元素
q.push({a,b}); // pair插入
q.emplace(); // 构造一个元素并插入队列
q.pop(); // 弹出队头元素
q.swap(); // 交换内容

字符串：

KMP

详解：KMP算法讲解-CSDN博客

#include<iostream>
using namespace std;

const int N = 1e5 + 10, M = 1e6 + 10;

int n, m;
char p[N], s[M];
int ne[N];

int main(){
    cin >> n >> p + 1 >> m >> s + 1;
    for(int i = 2, j = 0; i <= n; i ++ ){
        while(j && p[i] != p[j + 1]) j = ne[j];   
        if(p[i] == p[j + 1]) j ++;
        ne[i] = j;
    }

    for(int i = 1, j = 0; i <= m; i ++ ){
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) j ++ ;
        if(j == n){ 
            cout << i - n << ' ';
            j = ne[j];
        }
    }
    return 0;
}

传送门

831. KMP字符串 - AcWing题库

字符哈希

给定一个长度为 n 的字符串，再给定 m 个询问，每个询问包含四个整数 l1,r1,l2,r2，请你判断 [l1,r1]和 [l2,r2]这两个区间所包含的字符串子串是否完全相同。

思路： P进制来存储前缀和，然后访问区间通过乘除

#include <iostream>
#include <algorithm>

using namespace std;

typedef unsigned long long ULL;

const int N = 100010, P = 131;

int n, m;
char str[N];
ULL h[N], p[N];

ULL get(int l, int r) {
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s", str + 1);

    p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }

    while (m -- )
    {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);

        if (get(l1, r1) == get(l2, r2)) puts("Yes");
        else puts("No");
    }

    return 0;
}

传送门

841. 字符串哈希 - AcWing题库

字典树

应用：

• 字符串检索
• 词频统计
• 字典序排序
• 前缀匹配

构造：

struct TrieNode {
    <Type> data;
    bool isEndOfWord;
    TrieNode *children[SIZE];
}

#include <bits/stdc++.h>
using namespace std;

const int N = 800000;

struct node {
    bool repeat;
    int son[26];
    int num;
    bool isend;
} t[N];

int cnt = 1;
void Insert(char *s) {
    int now = 0;
    for(int i = 0; s[i]; i++) {
        int ch = s[i] - 'a';
        if(t[now].son[ch] == 0) 
            t[now].son[ch] = cnt++;
        now = t[now].son[ch];
        t[now].num++;
        if(i == strlen(s) - 1) t[now].isend = true;
    }
}

int Find(char *s) {
    int now = 0;
    for(int i = 0; s[i]; i++) {
        int ch = s[i] - 'a';
        if(t[now].son[ch] == 0) return 3;
        now = t[now].son[ch];
    }
    if(t[now].isend == false) return 3;
    if(t[now].num == 0) return 3;
    if(t[now].repeat == false) {
        t[now].repeat = true;
        return 1;
    }
    return 2;
}

int main() {
    char s[51];
    int n;
    cin >> n;
    while(n--) {
        cin >> s;
        Insert(s);
    }
    int m;
    cin >> m;
    while(m--) {
        cin >> s;
        int r = Find(s);
        if(r == 1) cout << "OK\n";
        else if(r == 2) cout << "REPEAT\n";
        else if(r == 3) cout << "WRONG\n";
    }
    return 0;
}

传送门

洛谷 P2580

搜索

DFS

深度优先搜索，换而言之就是递归遍历

思路： 递归遍历，同时进行[HTML_REMOVED]标记已经用过的点[HTML_REMOVED]，递归下一次，同时如果遍历结束要[HTML_REMOVED]恢复现场[HTML_REMOVED]

全排列

void dfs(int u){
    if(u == n){ 
        for(int i = 0; i < n; i ++ ) cout << path[i] << " ";
        cout << endl;
        return;
    }

    for(int i = 1; i <= n; i ++ ){
        if(st[i] == false) {
            path[u] = i;
            st[i] = true;
            dfs(u + 1);
            st[i] = false;
        }
    }
}

传送门

842. 排列数字 - AcWing题库

BFS

宽度优先搜素，换而言之就是遍历完当前情况在遍历下一重情况

思路： 重重遍历，把当前状态的所有情况考虑完，在考虑下一种情况，不需要恢复现场，常用于最短路径搜索

走迷宫

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 110;

int n, m;
int g[N][N], d[N][N];

int bfs() {
    queue<PII> q;

    memset(d, -1, sizeof d);
    d[0][0] = 0;
    q.push({0, 0});

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    while(q.size()) {
        PII t = q.front();
        q.pop();

        for(int i = 0; i < 4; i++) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if(x < 0 || y < 0 || x >= n || y >= m) continue;
            if(d[x][y] == -1 && g[x][y] == 0) {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
    }
    return d[n - 1][m - 1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            cin >> g[i][j];

    cout << bfs() << endl;

    return 0;
}

BFS通常和优先队列一起使用

传送门

842. 排列数字 - AcWing题库

844. 走迷宫 - AcWing题库

搜素的题目很多，因为可以和很多算法结合在一起考虑

双向广搜

思路： 双向广搜（BFS）可以让搜索的情况变少，（一个圆的半径是6，搜索到边界的探寻面积就是3.14*36，但是两个圆的半径是3，两个圆的探寻面积才3.14 * 9 * 2）

void two_BFS(int s, int f) { // s起点 f终点
    queue<int> a, b;
    a.push(s);
    b.push(f);
    while(a.size() && b.size()) {
        if(a.size() < b.size()) {
            extend(a.front());
            a.pop();
            // 探索a
        }
        else {
            extend(b.front());
            b.pop();
            // 探索b
        }
    }
}

剪枝

把它拿出来单独讲，是因为它同时出现在BFS，DFS中，这里不提具体的代码，但给出几份剪枝样例

剪枝大意： 把已经不满足的情况直接淘汰，不继续遍历

• 要求遍历从1~10中所有加起来等于15的情况个数（每个数最多使用一次可不用）（例1+9+5，10+5等等），那么如果说遍历到了1+9+6，已经大于15了，我们就没必要继续遍历后面的数了
• BFS搜索最短路时，如果当前的路径比之前已经探寻的最短路径长，那么也没有探寻该路径的必要了，剪掉（假设所有路径都是正数）

DFS的剪枝技术：可行性剪枝，搜索顺序剪枝，最优性剪枝，排除等效冗余，记忆化搜索等

BFS的剪枝技术：判重，使用优先队列有时候会产生奇效

图论

Dijkstra

Dijkstra求最短路1

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

思路： 先找到距离原点1最近的一个点，然后使用该点去更新其他的点，同时对该点进行标记，被标记的点则无需在经过处理（因为本身就是距离原点最近的点了），重复操作直到所有的点都被确定下来，时间复杂度o(n^2).

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 510;

int g[N][N]; // 图
int dist[N]; // 原点到每一个点的距离
bool st[N]; // 是否已经确定最短距离

int n, m;

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist); // 所有的点的距离全部赋值为最大值
    dist[1] = 0; // 原点本身距离原点为0

    for(int i = 0; i < n; i ++ ) {
        int t = -1; 
        for(int j = 1; j <= n; j ++ ) {
            if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j; // 找到未被使用的最小距离（距离原点）
        }
        st[t] = true; // 确定该点的距离不再改变

        for(int j = 1; j <= n; j ++ ) { 
            dist[j] = min(dist[j], dist[t] + g[t][j]); // 用该点更新其他所有点的状态
        }
    }

    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g); // 初始化图

    for(int i = 0; i < m; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c); // 重边处理
    }

    cout << dijkstra() << endl;

    return 0;
}

Dijkstra求最短路2

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

思路： 通过优先队列实现小根堆的操作，每次找到的是一个距离原点最近的值，通过优先队列（操作过程类似于bfs），去遍历整个稀疏图，直到所有的点都已经被遍历到，时间复杂度为o(mlogn)，m为边，n为点。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue> 

using namespace std;

typedef pair<int, int> PII; 

const int N = 1e6 + 10;

int h[N], e[N], ne[N], idx; // 图的存储
int w[N]; // 权重
int dist[N]; // 距离
bool st[N]; // 是否已经确定的最短距离

int n, m;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra() {
    memset(dist, 0x3f, sizeof(dist)); // 初始化
    dist[1] = 0;

    priority_queue<PII, vector<PII>, greater<PII>> heap; // 优先队列，小根堆，以第一个数大小排序
    heap.push({0, 1}); // 将1这个点的距离赋值为0 同时将这个类似于点的东西加入优先队列

    while(heap.size()) // 队列不空
    {
        PII t = heap.top();
        heap.pop();
        int ver = t.second, distance = t.first; // ver是点， distance 是原点到点的距离

        if(st[ver]) continue; // 会有很多不必要的点加入队列，如果前面出现后面就不需要判断
        st[ver] = true;

        for(int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > distance + w[i]) // 入队列的条件
            {
                dist[j] = distance + w[i];
                heap.push({dist[j], j}); // 可能会反复入队，但是没有关系
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];

}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;

    while(m -- ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

传送门

849. Dijkstra求最短路 I - AcWing题库

850. Dijkstra求最短路 II - AcWing题库

Spfa

给定一个 𝑛 个点 𝑚 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路，有则输出Yes，否则No

输入

第一行包含整数 𝑛 和 𝑚。

接下来 𝑚 行每行包含三个整数 𝑥,𝑦,𝑧，表示存在一条从点 𝑥 到点 𝑦 的有向边，边长为 𝑧。

思路：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 2010, M = 10010;

int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa()
{
    queue<int> q;

    for(int i = 1; i <= n; i ++ ) {
        st[i] = true;
        q.push(i);
    }

    while(q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;

        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;

                if(cnt[j] >= n) return true;
                if(!st[j]) 
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return false;
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);

    while(m --) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    if(spfa()) puts("Yes");
    else puts("No");

    return 0;
}

传送门

852. spfa判断负环 - AcWing题库

数学知识

质数

判定质数

思路： 从比它小的数中判断其是否为它的约数

技巧： i <= x / i 可以将o（n) 的时间复杂度降到o(sqrt(n))，同时，不写成i * i <= x可以防止i * i溢出,不写成i <= sqrt(n)可以少每次的sqrt函数调用，减少用时

bool is_prime(int x){
    if(x < 2) return false;
    for(int i = 2; i <= x / i; i ++ ){
        if(x % i == 0) return false;
    }
    return true;
}

分解质因数

思路： 合数一定可以分解为质数相乘，那么将一个数除尽每一个质数即可分解该数

void divide(int n){
    for(int i = 2; i <= n / i; i++){
        if(n % i == 0){
            int s = 0;
            while(n % i == 0){
                n /= i;
                s ++;
            }
            cout << i << " " << s << endl;
        }
    }
    if(n > 1) cout << n << " 1" << endl;
    cout << endl;
}

筛质数

埃式筛法

思路：一个数如果不是质数，一定会被其前面小于它的质数给筛掉，（合数可以分解为质数相乘），时间复杂度o(nlogn)

//primes数组用来存放质数
//st[i], i为质数则为false否则为true
int primes[N], cnt;
bool st[N];

void get_prime(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt ++ ] = i;
            for(int j = i; j <= n; j += i) st[j] = true;
        }
    }
}

线性筛

思路：比埃式筛法快的原因是因为埃式筛法可能会把一个数多次筛掉，而线性筛只筛依次，时间复杂度o(n)

bool st[N];
int primes[N], cnt;

void get_prime(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n / i; j ++ ){
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}

传送门

866. 试除法判定质数 - AcWing题库

867. 分解质因数 - AcWing题库

868. 筛质数 - AcWing题库

约数

试除法

思路： 将它所有的约数直接统计并输出

vector<int> get_divisors(int n){
    vector<int> ans;
    for(int i = 1; i <= n / i; i ++ ) {
        if(n % i == 0) {
            ans.push_back(i);
            if(i != n / i) ans.push_back(n / i);
        }
    }
    sort(ans.begin(), ans.end());
    return ans;
}

最大公约数

思路： 辗转相除法（辗转相减法时间复杂度较高）

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a; // 辗转相除法
}

传送门

869. 试除法求约数 - AcWing题库

872. 最大公约数 - AcWing题库

快速幂

纯快速幂

思路： 将b分解为二进制形式，然后遍历二进制，如果该位为1，则乘上a（a是变化的，每一次操作将a扩大成a的平方倍）

ll qmi(ll a, ll k, ll p)
{
    ll res = 1;
    while(k) 
    {
        if(k & 1) res = res * a % p; 
        k >>= 1; 
        a = a * a % p; // 将a扩大平方倍
    }
    return res;
}

快速幂求逆元

逆元：除以一个数求余等于乘上这个逆元再求余

【由于求余法则中没有除法的规定，我们只能通过逆元来求余】

乘法逆元的定义

若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a/b≡a×x(mod m)，则称 x 为 b 的模 m 乘法逆元，记为 b−1(mod m)。

b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，b^m−2即为 b 的乘法逆元。

由此可知，求逆元的方式同快速幂，只需要将指数改为p-2即可

#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;

ll qmi(ll a, ll b, ll p)
{
    ll res = 1;
    while(b)
    {
        if(b & 1) res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    while(n -- )
    {
        ll a, p;
        cin >> a >> p;
        if(a % p == 0) cout << "impossible" << endl;
        else cout << qmi(a, p - 2, p) << endl;
    }
    return 0;
}

传送门

875. 快速幂 - AcWing题库

876. 快速幂求逆元 - AcWing题库

欧拉函数

欧拉函数：1~N中与N互质的数的个数被称为欧拉函数，记为 ϕ(N)。

欧拉函数

公式： phi = 质数分之质数-1之积

思路： 通过试除法找到质数，然后套用公式

int phi(int x) {
    int res = x;
    for(int i = 2; i <= x / i; i++) {
        if(x % i == 0) {
            res = res / i * (i - 1);
            while(x % i == 0) x /= i;
        }
    }
    if(x > 1) res = res / x * (x - 1);
    return res;
}

筛法求欧拉函数

详解：AcWing 874. 筛法求欧拉函数 - AcWing

• 互质 ：两个数的最大公约数是1

• 欧拉函数是积性函数

• 结论：若a与n互质，则a^ϕ(n) mod n == 1

#include<iostream>

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;

int primes[N], cnt;
int phi[N];
bool st[N];

void get_eulers(int n)
{
    phi[1] = 1;
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])
        {
            primes[cnt ++ ] = i;
            phi[i] = i - 1; 
        }
        for(int j = 0; primes[j] <= n / i; j++)
        {
            int t = primes[j] * i;
            st[t] = true;
            if(i % primes[j] == 0)
            {
                phi[t] = phi[i] * primes[j]; 
                break;
            }
            phi[t] = phi[i] * (primes[j] - 1); 
        }
    }
}

int main()
{
    int n;
    cin >> n;
    get_eulers(n);

    ll res = 0;
    for(int i = 1; i <= n; i++) res += phi[i];

    cout << res << endl;

    return 0;
}

传送门

873. 欧拉函数 - AcWing题库

874. 筛法求欧拉函数 - AcWing题库

扩展欧几里得

扩展欧几里得算法

求出一组x,y，使得a * x + b * y == gcd(a, b)

void exgcd(int a, int b, int &x, int &y) {
    if(!b) {
        x = 1, y = 0;
        return ;
    }
    exgcd(b, a % b, y, x);
    y = y - a / b * x;
}

线性同余方程

求一个x，满足a * x == b(mod m)

思路： 通过扩展欧几里得算法的思想，将题目意思转换为a * x+m * y==gcd(a, m)求x，同时如果gcd无法被b整除，则说明无解。

#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if(!b)
    {
        x = 1, y = 0; // 边界，（或理解为递归的重点）
        return a;
    }
    int d = exgcd(b, a % b, y, x);// y与b对应，x与a对应
    y -= a / b * x;// 公式推导
    return d;
}

int main()
{
    int n;
    cin >> n;
    while(n -- )
    {
        ll a, b, m;
        cin >> a >> b >> m;
        ll x, y;
        ll t = exgcd(a, m, x, y);
        if(b % t) puts("impossible");
        else cout << x * (b / t) % m << endl;
    }
    return 0;
}

传送门

877. 扩展欧几里得算法 - AcWing题库

878. 线性同余方程 - AcWing题库

博弈论

详解：博弈论详解（Nim游戏，台阶-Nim游戏，集合-Nim游戏，拆分-Nim游戏-CSDN博客

思路： 所有结果在开始的时候就已经注定好了，所以只需要找到这种平衡关系，构造平衡：后手随先手动能够让先手永远处于必输状态

Nim游戏：

n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

int main()
{
    int n;
    cin >> n;
    int res = 0;
    for(int i = 0; i < n; i ++ )
    {
        int t;
        cin >> t;
        res ^= t;
    }
    if(res) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

台阶-Nim游戏：

现在，有一个 n 级台阶的楼梯，每级台阶上都有若干个石子，其中第 i 级台阶上有 ai 个石子(i≥1)。两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

int main()
{
    int n;
    cin >> n;
    int res = 0;
    for(int i = 1; i <= n; i ++ )
    {
        int t;
        cin >> t;
        if(i % 2 != 0) res ^= t; 
    }
    if(res) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

集合-Nim游戏：

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_set>
using namespace std;

const int N = 110, M = 10010;

int n, m;
int s[N], f[M];

int sg(int x)
{
    if(f[x] != -1) return f[x]; // 如果已经存在则不需要二次遍历

    unordered_set<int> S; // 定义一个集合存储情况
    for(int i = 0; i < m; i ++ )
    {
        int sum = s[i]; // 每一种取出方式
        if(x >= sum) S.insert(sg(x - sum)); // 如果数量大于这种取出方式，则递归取出了这个方式的情况，同时把这种取出方式的sg值放入集合
    }

    for(int i = 0; ; i ++ )
    {
        if(!S.count(i)) return f[x] = i;//s.count(i)，判断集合中是否存在该元素
    }
}

int main()
{
    cin >> m;
    for(int i = 0; i < m; i ++ ) cin >> s[i];
    cin >> n;

    memset(f, -1, sizeof f); // 初始化

    int  res = 0;
    for(int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if(res) puts("Yes"); // 如果不为0，说明先手可以变为0从而成为后手，让原来的后手输
    else puts("No");

    return 0;
}

拆分-Nim游戏：

给定 n 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为 0，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

辅助理解题意：可以是任意两堆大小的新堆（只要满足堆的石子数量小于取走的即可，两堆放入的总和可以大于取走的）

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_set>

using namespace std;

const int N = 110;

int n;
int f[N];

int sg(int x)
{
    if(f[x] != -1) return f[x];

    unordered_set<int> S;
    for(int i = 0; i < x; i ++ ) // 两重循环，遍历所有可能的sg情况
    {
        for(int j = 0; j <= i; j ++ ) 
        {
            S.insert(sg(i) ^ sg(j));
        }
    }

    for(int i = 0; ; i ++ ) 
    {
        if(!S.count(i)) return f[x] = i;
    }
}

int main()
{
    cin >> n;
    memset(f, -1, sizeof f);

    int res = 0;
    while(n -- )
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }

    if(res) puts("Yes");
    else puts("No");

    return 0;
}

传送门

891. Nim游戏 - AcWing题库

892. 台阶-Nim游戏 - AcWing题库

893. 集合-Nim游戏 - AcWing题库

894. 拆分-Nim游戏 - AcWing题库

高斯消元

代办

求组合数

给定a,b求$C_{a}^{b}$

求组合数I（小数）

数据范围

1≤n≤10000
1≤b≤a≤2000

公式： $C_{a}^{b}$ = $C_{a - 1}^{b - 1}$ + $C_{a - 1}^{b}$

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 2010, mod = 1e9 + 7;

int c[N][N];

void init() {
    for(int i = 0; i < N; i++) {
        for(int j = 0; j <= i; j++) {
            if(!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }
}

int main()
{
    int n;
    init();

    cin >> n;
    while(n--) {
        int a, b;
        cin >> a >> b;
        cout << c[a][b] << endl;
    }
    return 0;
}

求组合数II（大数）

数据范围

1≤n≤10000
1≤b≤a≤10^5^

公式： $C_{a}^{b}$ = $\frac{a!}{b!(a - b)!}$ = a! * b!^-1^ * (a - b) !^-1^

思路： 快速幂求逆元

#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10, mod = 1e9 + 7;

ll fact[N], infact[N]; // infact表示除数的逆元

ll qmi(ll a, ll k, ll p)
{
    ll res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        a = a * a % p;
        k >>= 1;
    }
    return res;
}

int main(){
    fact[0] = infact[0] = 1;
    for(int i = 1; i < N; i++)
    {
        fact[i] = fact[i - 1] * i % mod;
        infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }

    int n;
    cin >> n;
    while(n--)
    {
        ll a, b;
        cin >> a >> b;
        cout << fact[a] * infact[b] % mod * infact[a - b] % mod << endl;
    }
    return 0;
}

求组合数III(大大数)

数据范围

1≤n≤20
1≤b≤a≤10^18^
1≤p≤10^5^

公式： lucas

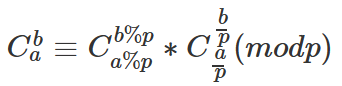
#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

ll qmi(ll a, ll k, ll p)
{
    ll res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        a = a * a % p;
        k >>= 1;
    }
    return res;
}

ll C(ll a, ll b, ll p)
{
    if(b > a) return 0;

    ll res = 1;
    for(int i = 1, j = a; i <= b; i ++ , j -- )
    {
        res = res * j % p;
        res = res * qmi(i, p - 2, p) % p;
    }
    return res;
}

ll lucas(ll a, ll b, ll p)
{
    if(a < p && b < p) return C(a, b, p);
    return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

int main()
{
    int n;
    cin >> n;
    while(n -- )
    {
        ll a, b, p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }
    return 0;
}

求组合数IV（高精度）

传送门

885. 求组合数 I - AcWing题库

886. 求组合数 II - AcWing题库

887. 求组合数 III - AcWing题库

动态规划

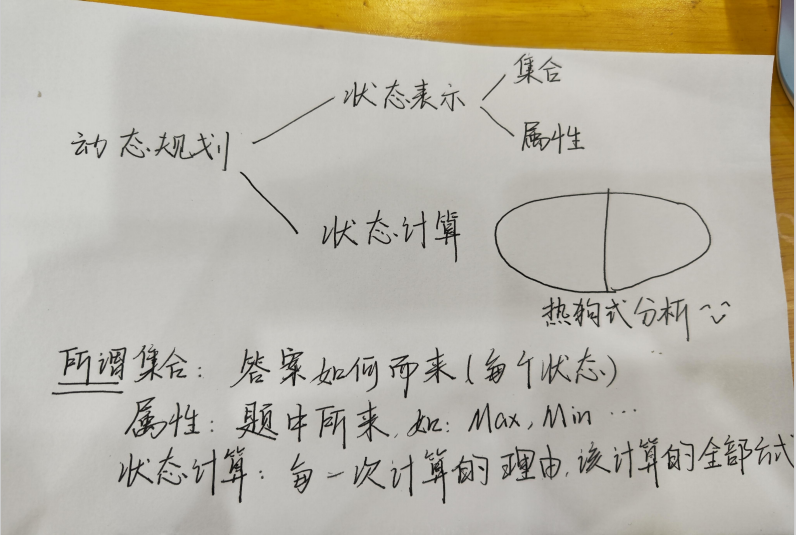
（注：y式dp法）

背包问题

详解： 背包问题合集-CSDN博客

01背包

思路： 01背包中，每个元素都只能被使用一次，正常情况下，我们使用二维存储，每一次都添加一名新元素，将其转为一维，从后往前遍历就不会多次使用同一个元素

二维

int n, m; // 数量，体积
int v[N], w[N]; // 容量，价值
int f[N];  // f[i]容量为i的最大价值

for(int i = 1; i <= n; i ++ ) {
        for(int j = 1; j <= m; j ++ ) {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);  
        }
    }

一维

int n, m; // 数量，体积
int v[N], w[N]; // 容量，价值
int f[N];  // f[i]容量为i的最大价值

for(int i = 1; i <= n; i ++ ) {
    for(int j = m; j >= v[i]; j -- ) {
        f[j] = max(f[j], f[j - v[i]] + w[i]);
    }
}

完全背包问题

思路： 每个元素可以被多次使用，所以一维状态下从前往后遍历

int n, m;
int v[N], w[N];
int f[N];

for(int i = 1; i <= n; i ++ ) {
    for(int j = v[i]; j <= m; j ++ ) {
        f[j] = max(f[j], f[j - v[i]] + w[i]);
    }
}

多重背包问题

思路： 二进制分解（只放最优方式，后面链接有详解），把一个元素的个数分解为2进制形式，然后将其价值变成其倍数，转为01背包形式

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 12010, M = 2010; // N = n * logn

/* 思想：通过二进制想法，将一个拥有很多的物品分解为logn个物品
进行处理，这logn个物品可以通过组合达到满足任意个该物品的数量*/

int n, m;
int v[N], w[N];
int f[M];

int main()
{
    cin >> n >> m;

    int cnt = 0; // 下标
    for(int i = 0; i < n; i ++ ) {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s)  
        {
            v[cnt] = k * a;
            w[cnt ++ ] = k *b;
            s -= k;
            k *= 2;
        }
        if(s > 0) {
            v[cnt] = s * a;
            w[cnt ++ ] = s *b;
        }
    }
    n = cnt;
    for(int i = 0; i < n; i ++ ) { // 01背包思路
        for(int j = m; j >= v[i]; j -- ) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

### 分组背包问题

思路： 三重循环暴力求解，先遍历组，再遍历容量（从后往前），再遍历该组元素（在同一个容量内遍历组内，即可保证元素只使用一个最优的）

int n, m;
int v[N][N], w[N][N], s[N]; // v,w 表示第几组的第几个物品的体积和价值 ， s 每组元素个数
int f[N]; // 容量为j 可放的最大价值

for(int i = 1; i <= n; i ++ ) { // 第 i 组
    for(int j = m; j >= 0; j -- ) { // 容量为 j
        for(int k = 0; k < s[i]; k ++ ) { // 该组第 k 个
            if(v[i][k] <= j) {
                f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
            }
        }
    }
}

传送门

2. 01背包问题 - AcWing题库

3. 完全背包问题 - AcWing题库

5. 多重背包问题 II - AcWing题库

9. 分组背包问题 - AcWing题库

线性DP

代办

详解： 线性DP（数字三角形，最长上升子序列，最长公共子序列，最短编辑距离，编辑距离-CSDN博客

代办

高级数据结构

很重要的东西，所以我把它放在最后一部分咯

并查集

思路： 把具有同一属性的元素放在一起，成为一个集合，主要用于处理不相交集合的合并问题

使用前初始化：

for(int i = 1; i <= n; i++) p[i] = i;

板子

int p[N]; 

int find(int x) {
    if(p[x] == x) return p[x];
    return p[x] = find(p[x]); // 同时完成路径压缩
}

// 合并a, b
p[find(a)] = find(b);

// 查询a，b是否同一集合
if(find(a) == find(b))

传送门

528. 奶酪 - AcWing题库

树状数组

思路： 树状数组可以做的事：区间查询，单点修改，同时也可以把归并排序求逆序对的工作也包揽了

树状数组板子

int tr[N];

int lowbit(int x) { // 从后往前返回二进制中的第一个1
    return x & -x;
}

void add(int x, int k) { // 单点修改
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += k;
}

int query(int x) { // 区间查询
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

可以用来求逆序对：一个数要交换几次取决于它左边有多少个比它大的数以及右边有多少个比它小的数

传送门

1265. 数星星 - AcWing题库

线段树

思路：”分治法 + 二叉树结构+Lazy-Tag技术“ 。线段树可以做的事：区间查询，区间修改

Lazy-Tag: 若修改的是一个线段区间，就只对这个线段区间进行整体上的修改，其内部每个元素先不进行修改，只有当这个线段区间的一致性被破坏时，才把变化值传给子区间

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 1e5 + 10;
ll a[MAXN];      //记录数列的元素，从a[1]开始
ll tree[MAXN<<2];//tree[i]：第i个结点的值，表示一个线段区间的值，例如最值、区间和
ll tag[MAXN<<2]; //tag[i]：第i个结点的lazy-tag，统一记录这个区间的修改
ll ls(ll x){ return x<<1;  }     //定位左儿子：x*2
ll rs(ll x){ return x<<1|1;}     //定位右儿子：x*2 + 1
void push_up(ll p){              //从下往上传递区间值
    tree[p] = tree[ls(p)] + tree[rs(p)]; 
     //本题是区间和。如果求最小值，改为：tree[p] = min(tree[ls(p)], tree[rs(p)]);
}
void build(ll p,ll pl,ll pr){    //建树。p是结点编号，它指向区间[pl, pr]
    tag[p] = 0;                  //lazy-tag标记
    if(pl==pr){tree[p]=a[pl]; return;}  //最底层的叶子，赋值    
    ll mid = (pl+pr) >> 1;       //分治：折半
    build(ls(p),pl,mid);         //左儿子
    build(rs(p),mid+1,pr);       //右儿子
    push_up(p);                  //从下往上传递区间值
} 
void addtag(ll p,ll pl,ll pr,ll d){   //给结点p打tag标记，并更新tree
    tag[p] += d;                   //打上tag标记
    tree[p] += d*(pr-pl+1);        //计算新的tree
}
void push_down(ll p,ll pl,ll pr){     //不能覆盖时，把tag传给子树
    if(tag[p]){                       //有tag标记，这是以前做区间修改时留下的
        ll mid = (pl+pr)>>1; 
        addtag(ls(p),pl,mid,tag[p]);    //把tag标记传给左子树
        addtag(rs(p),mid+1,pr,tag[p]);  //把tag标记传给右子树
        tag[p]=0;                       //p自己的tag被传走了，归0
    }
}
void update(ll L,ll R,ll p,ll pl,ll pr,ll d){ //区间修改：把[L, R]内每个元素加上d
    if(L<=pl && pr<=R){  //完全覆盖，直接返回这个结点，它的子树不用再深入了    
        addtag(p, pl, pr,d);  //给结点p打tag标记，下一次区间修改到p这个结点时会用到
        return;                    
    }
    push_down(p,pl,pr);             //如果不能覆盖，把tag传给子树
    ll mid=(pl+pr)>>1;
    if(L<=mid) update(L,R,ls(p),pl,mid,d);    //递归左子树
    if(R>mid)  update(L,R,rs(p),mid+1,pr,d);  //递归右子树
    push_up(p);                               //更新
}
ll query(ll L,ll R,ll p,ll pl,ll pr){
           //查询区间[L,R]；p是当前结点（线段）的编号，[pl,pr]是结点p表示的线段区间
    if(pl>=L && R >= pr) return tree[p];       //完全覆盖，直接返回
    push_down(p,pl,pr);                        //不能覆盖，递归子树
    ll res=0;
    ll mid = (pl+pr)>>1;
    if(L<=mid) res+=query(L,R,ls(p),pl,mid);   //左子节点有重叠
    if(R>mid)  res+=query(L,R,rs(p),mid+1,pr); //右子节点有重叠
    return res;
}
int main(){
    ll n, m; scanf("%lld%lld",&n,&m);
    for(ll i=1;i<=n;i++)  scanf("%lld",&a[i]);
    build(1,1,n);                   //建树
    while(m--){
        ll q,L,R,d;
        scanf("%lld",&q);
        if (q==1){                   //区间修改：把[L,R]的每个元素加上d
           scanf("%lld%lld%lld",&L,&R,&d);
           update(L,R,1,1,n,d); 
        }
        else {                        //区间询问：[L,R]的区间和
           scanf("%lld%lld",&L,&R);
           printf("%lld\n",query(L,R,1,1,n));   
        }       
    }
    return 0;
}

（注：代码来自罗永军算法竞赛）

传送门

P3372 【模板】线段树 1 - 洛谷