我们常常遇到一些图论题目要求特殊操作。
但我们蒟蒻不会 tarjan 缩点,不会拓扑排序，或者各种高深的技巧。。
下面介绍一种优雅的暴力——分层图暴力建图加边

分层图

分层图，顾名思义，就是一层一层的图。好像有什么不对

我们把构造的图看成一层，将它复制，就有了很多层一模一样的图。好像没什么用

这个时候，如果我们要对单点进行一些不可说明的操作，我们就将操作转化为一条边，沟通我们之前的很多层图。

废话不多说，上例题：

例题 1 : 飞行路线

题目描述

Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在n个城市设有业务，设这些城市分别标记为0到n−1，一共有m种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice和Bob现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多kk种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少？

分析：

这是一道分层图模板题。

我们把免费操作转化成零边，如果进行免费操作，就进入下一层
如图：

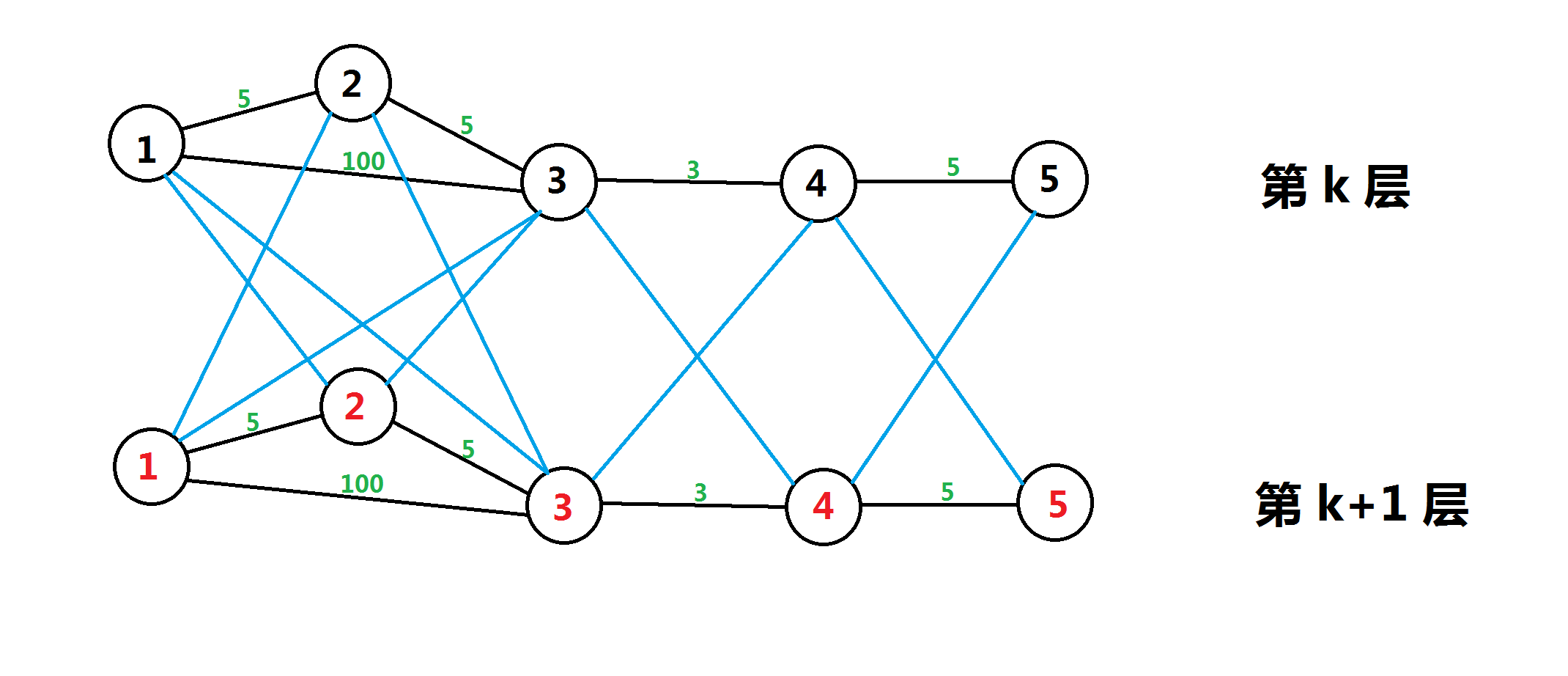
蓝边就是零边

建 k + 1 层图，如果执行免费操作就进入下一层。

总共有 k + 1 层，对应 k 次操作。因为每层都是一样的所以最终在 k + 1 层的累计的花费就是所求

关于建图：

    for(int i=0,x,y,z;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z),add(y,x,z);
        for(int j=1,z1=0;j<=k;j++)
        {
            add(x+(j-1)*n,y+j*n,z1);
            add(y+(j-1)*n,x+j*n,z1);
            //j-1层 和 j层 间的建边
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);
            //j层 的建边
        }
    }

    for(int i=1,z=0;i<=k;i++)
        add(t+(i-1)*n,t+i*n,z);
    //防止毒瘤数据，k 次机会还没用完就到终点了。。

分层图的建图大致相同，只是对特殊边的处理不同

代码

#include <bits/stdc++.h>
using namespace std;

const int N=110000+10,M=2500000+10;

int n,m,k,s,t;
int tot=0;

priority_queue< pair <int ,int> > q;

struct node
{
    int ver,nex,edge;
}po[M];
int head[N],dis[N];
bool v[N];

void add(int x,int y,int z)
{
    po[++tot].ver=y,po[tot].edge=z;
    po[tot].nex=head[x],head[x]=tot;
}

void dijkstra(int str)
{
    memset(dis,0x3f,sizeof(dis));
    dis[str]=0;
    q.push(make_pair(0,str));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(v[x]) continue;
        v[x]=true;
        for(int i=head[x];i;i=po[i].nex)
        {
            int y=po[i].ver,z=po[i].edge;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                q.push(make_pair(-dis[y],y));
            }
        }
    }
}
//普普通通的模板

int main() {
    scanf("%d%d%d",&n,&m,&k);
    scanf("%d%d",&s,&t);

    for(int i=0,x,y,z;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z),add(y,x,z);
        for(int j=1,z1=0;j<=k;j++)
        {
            add(x+(j-1)*n,y+j*n,z1);
            add(y+(j-1)*n,x+j*n,z1);
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);
        }
    }

    for(int i=1,z=0;i<=k;i++)
        add(t+(i-1)*n,t+i*n,z);

    dijkstra(s);

    printf("%d",dis[t+k*n]);

    return 0;
}

学会了优雅暴力的分层图，我们就可以去轻松地切掉其他题了

例题 2 电话线 Telephone Lines ( 通信线路 )

题目描述

在郊区有 N 座通信基站，P 条双向电缆，第 i 条电缆连接基站Ai和Bi。

特别地，1 号基站是通信公司的总站，N 号基站位于一座农场中。

现在，农场主希望对通信线路进行升级，其中升级第 i 条电缆需要花费Li。

电话公司正在举行优惠活动。

农产主可以指定一条从 1 号基站到 N 号基站的路径，并指定路径上不超过 K 条电缆，由电话公司免费提供升级服务。

农场主只需要支付在该路径上剩余的电缆中，升级价格最贵的那条电缆的花费即可。

求至少用多少钱可以完成升级。

分析

与上题类似,建图后,如果使用免费操作,就进入下一层
如图:

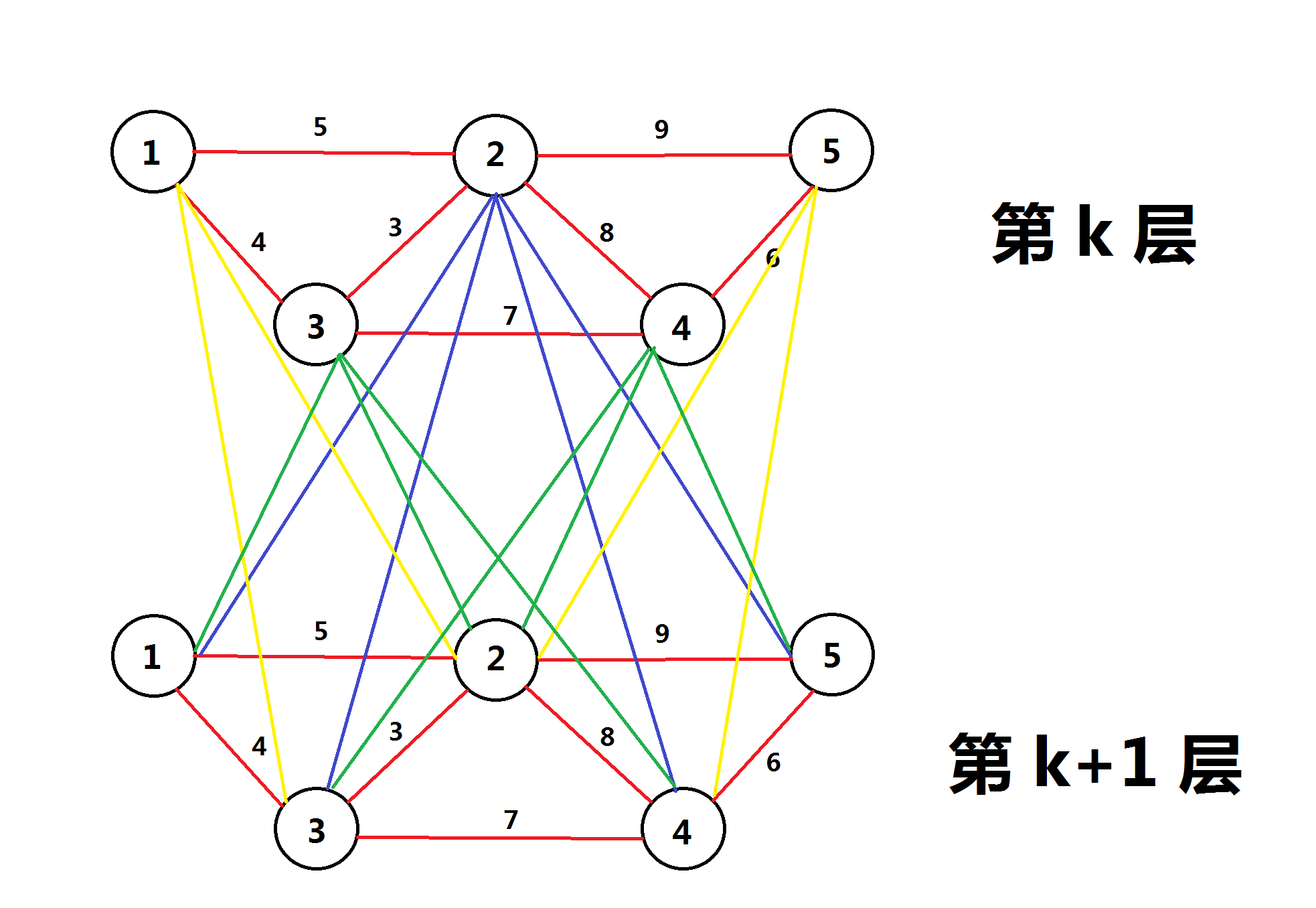
除红边外的边是零边

只要注意,最终花费是权值最大的边,所以求最短路时略有改动

代码

#include<bits/stdc++.h>
using namespace std;

const int N=1000000+10,M=10000000+10;

int n,p,k;
int tot=0;
priority_queue< pair<int ,int> > q;
struct node
{
    int ver,nex,edge;
}po[M];
int head[N],dis[N];
bool v[N];

void add(int x,int y,int z)
{
    po[++tot].ver=y,po[tot].edge=z;
    po[tot].nex=head[x],head[x]=tot;
}

void dijkstra()
{
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    q.push(make_pair(0,1));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(v[x]) continue;
        v[x]=true;
        for(int i=head[x];i;i=po[i].nex)
        {
            int y=po[i].ver,z=max(po[i].edge,dis[x]);
            //花费是权值最大的边
            if(dis[y]>z)
            {
                dis[y]=z;
                q.push(make_pair(-dis[y],y));
            }
        }
    }
}

int main()
{
    scanf("%d%d%d",&n,&p,&k);
    for(int i=1,x,y,z;i<=p;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
        for(int j=1,z1=0;j<=k;j++)
        {
            add(x+(j-1)*n,y+j*n,z1);
            add(y+(j-1)*n,x+j*n,z1);
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);
        }
    }
    for(int i=1,z=0;i<=k;i++)
        add(i*n,(i+1)*n,z);

    dijkstra();

    if(dis[(k+1)*n]==1061109567) printf("-1");
    else printf("%d",dis[(k+1)*n]);

    return 0;
}

连续切了两道题，而且差不多是模板，是不是有点小激动呢

例题 3 最优贸易

题目描述

C国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。

任意两个城市之间最多只有一条道路直接相连。

这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为1条。

C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。

但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到C国旅游。

当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚一点旅费。

设C国 n 个城市的标号从 1~n，阿龙决定从1号城市出发，并最终在 n 号城市结束自己的旅行。

在旅游的过程中，任何城市可以被重复经过多次，但不要求经过所有 n 个城市。

阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。

因为阿龙主要是来C国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。

请你告诉阿龙，他最多能赚取多少旅费。

分析

这道题目也可以用分层图做，只是建边的方式不同。

我们把相邻层 相同的点 相连。

图一共三层，第一层到第二层是花钱买，所以第一层与第二层的连边就是水晶球的价格

第二层到第三层是卖，所以第二层与第三层的连边就是 负的水晶球的价格 花费是负值（加钱）

然后又可以跑最短路了 开心 但是有负权，所以用 SPFA

代码

#include<bits/stdc++.h>
using namespace std;

const int N=100000+10,M=500000+10;

queue<int > q;
struct node
{
    int edge,nex,ver;
}po[M*2];
int head[N],dis[N],val[N];
bool v[N];
int n,m,tot=0;

void add(int x,int y,int z)
{
    po[++tot].ver=y;
    po[tot].edge=z;
    po[tot].nex=head[x];
    head[x]=tot;
}

void spfa()
{
    memset(dis,63,sizeof(dis));
    memset(v,0,sizeof(v));
    dis[1]=0;
    v[1]=true;
    q.push(1);
    while(q.size())
    {
        int x=q.front();
        q.pop();
        v[x]=0;
        for(int i=head[x];i;i=po[i].nex)
        {
            int y=po[i].ver,z=po[i].edge;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                if(!v[y]) q.push(y),v[y]=1;
            }
        }
    }
}

int main()
{
    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++) scanf("%d",&val[i]);

    for(int i=1,x,y,z;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        if(z==1)
        {
            add(x,y,0);
            //第一层
            add(x+n,y+n,0);
            //第二层
            add(x+n*2,y+n*2,0);
            //第三层
        }else
        {
            add(x,y,0); add(y,x,0);
            //第一层
            add(x+n,y+n,0); add(y+n,x+n,0);
            //第二层
            add(x+n*2,y+n*2,0); add(y+n*2,x+n*2,0);
            //第三层
        }
    }

    for(int i=1;i<=n;i++)
    {
        add(i,i+n,val[i]);
        //买
        add(i+n,i+n*2,-val[i]);
        //卖
    }

    spfa();

    if(dis[n*3]<0) printf("%d",-dis[n*3]);
    else printf("0");

    return 0;
}

三倍经验激不激动！！ 我怎么会告诉你题目洛谷里全有。

看完后如果觉得有帮助，就点个赞吧 (｀・ω・´)