前缀和、差分数组都是从i=1开始,注意考虑边界问题

前缀和

一维前缀和

一般都是插在题目里面使用
sum[i]+=sum[i-1];
1.均分纸牌问题
2.快速查询[l,r]段区间和
长度不超过m的最长子序列——> 102. 最佳牛围栏

二维前缀和

计算方法

sum[i][j]+=sum[i-1][j]+sum[i]j-1[]-sum[i-1][j-1]
计算方法算出来的前缀和是(1，1)到(x，y)的前缀和 所以一般还需要进行枚举对角端点(x1,y1)(x2,y2)(总是会不枚举直接用前缀和了,这样是不对的不能包含所有矩阵)
但是如果确定了length可以枚举左上端点,计算出右下端点,直接计算所需大小的所有矩形,通过前缀和来进行容斥计算 Acwing 99. 激光炸弹
枚举对角端点也可以简化成确定左边界,枚举上下边界和又边界的问题 AcWing 126. 最大的和

离散化

离散化思想:不在乎数字原本大小多少,只在乎数字间的相对大小关系(第一大,第二大....),从而把离散的点聚集起来变成连续的点
适用情况:数字大小常常比数据个数多很多
做法思考:要从题目中把所有可能用到的东西都放入num构成完整的离散化数组之后再进行判断

//离散化方法:
//譬如覆盖一个1-10000中的100个值不离散化可能需要开g[10000],但是离散只需要g[100]和num[100]
int find(int x) //映射到1,2,3,...,n上,找到第一个大于等于的数
{
    int l=0,r=num.size();
    while(l<r)
    {
        int mid=(l+r)>>1
        if(a[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1;
}
for(int i=0;i<n;i++)
{
    cin>>g[i];
    num.push(g[i]);

}
sort(num.begin(),num,end());
num.earse(num.begin(),num,end(),num.end());
for()
{
    int pos=lower_bound(num.begin(),num,end(),g[i])-num.begin();
    num[postion]=g[i];//因题目而定

}

Acwing 99. 赶牛入圈

存在的问题

1.激光炸弹和赶牛入圈反映的边界问题(求对应大小的矩形算式不同)
激光炸弹是要求不包括边界
res=sum[i+r][j+r]-sum[i][j+r]-sum[i+r][j]+sum[i][j]
赶牛入圈是包括边界
res=sum[i+r][j+r]-sum[i+r][j-1]-sum[i-1][j+r]+sum[i-1][j-1]
(直接减去[i]与[j],此时减去的部分就包含了当前矩形的边界了)
(而减去[i-1]和[j-1],此时向上移动了一格,所以不会删除边界)

差分

目前遇到的题目较前缀和较少,主要适用于对区间内数字进行统一修改 如:[l,r]区间数字统一+1)
求某项元素操作——>前缀和问题 D[n]——>A[n]——>S[n]

一维差分数组

• 注意一开始差分数组的初始化(差分数组初始化一般让各项全为0,然后依据题目而定,如果有统一数字h那么要让D[1]=h)
  • 普通的差分数组第1项为原来值,后面每项D[i]=a[i]-a[i-1]
  • AcWing 100. IncDec序列
  • 初始化差分数组为0,,根据题目要求实际上所有牛应该为h,那么h[1]=h;
    AcWing 101.最高的牛

或者可以理解成默认给定数组一开始元素全为0,但是实际上并不为0,就可以认为是在进行i到i区间的数组元素统一+a[i],这样就完成了默认差分数组的初始化;

int a[N],b[N];
int n,m;
void change(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        change(i,i,a[i]);
    }
    while(m--)
    {
        int l,r,c;
        cin>>l>>r>>c;
        change(l,r,c);
    }
    for(int i=1;i<=n;i++)
    {
        b[i]+=b[i-1];
        printf("%d ",b[i]);
    }


}

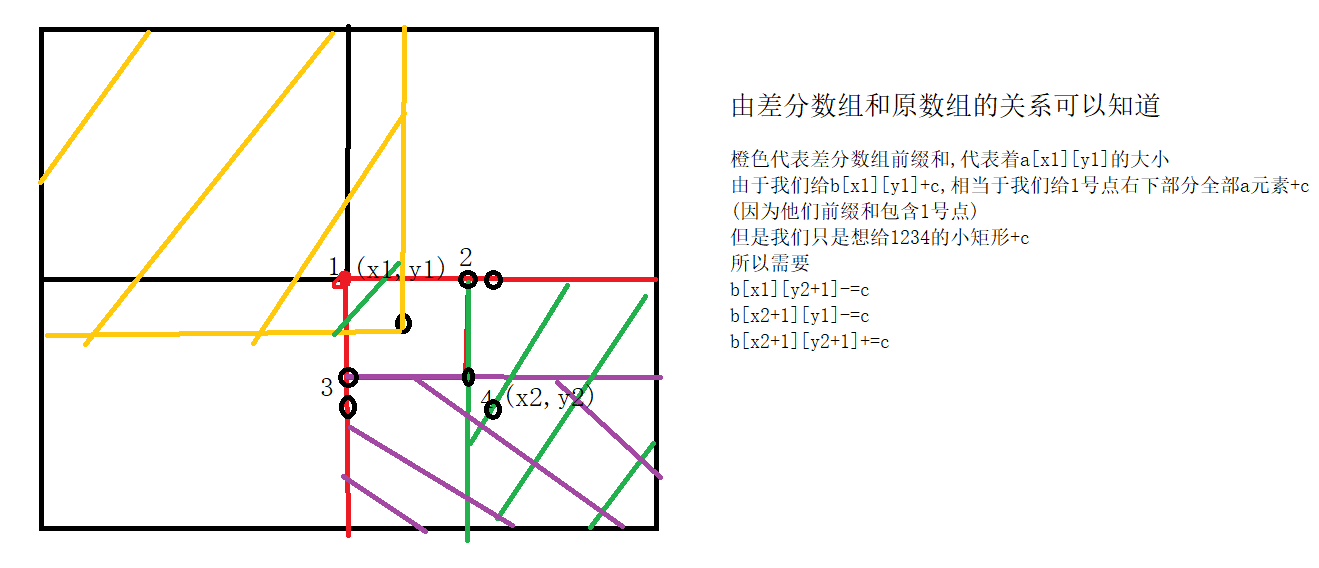
二维差分数组

#include<iostream>
int a[N],b[N];
int n,m,q;
void change(int x1,int y1,int x2,int y2)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;i<=m;j++)
        {
            cin>>a[i][j];
            change(i,j,i,j,a[i][j]);//初始化差分数组
        }
    }
    while(q--)
    {
        int l1,l2,r1,r2,c;
        cin>>l1>>r1>>l2>>r2>>c;
        change(l1,r1,l2,r2,c);//对围成的矩形进行统一操作
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;i<=m;j++)
        {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];//计算改变后的a[i][j]
            cout<<b[i][j];
        }
    }


}