区间问题
What is 贪心
贪心:每一次只在当前这一块选择局部最优解,但最后可以走到全局最优解,只有一个问题是单方的,才可以使用贪心算法
题目
Acwing.905 区间选点
举例:
如图,需要选两个点,每个区间都有一个点,第1、2、3个区间内有第一个点,第4个区间包含第二个点
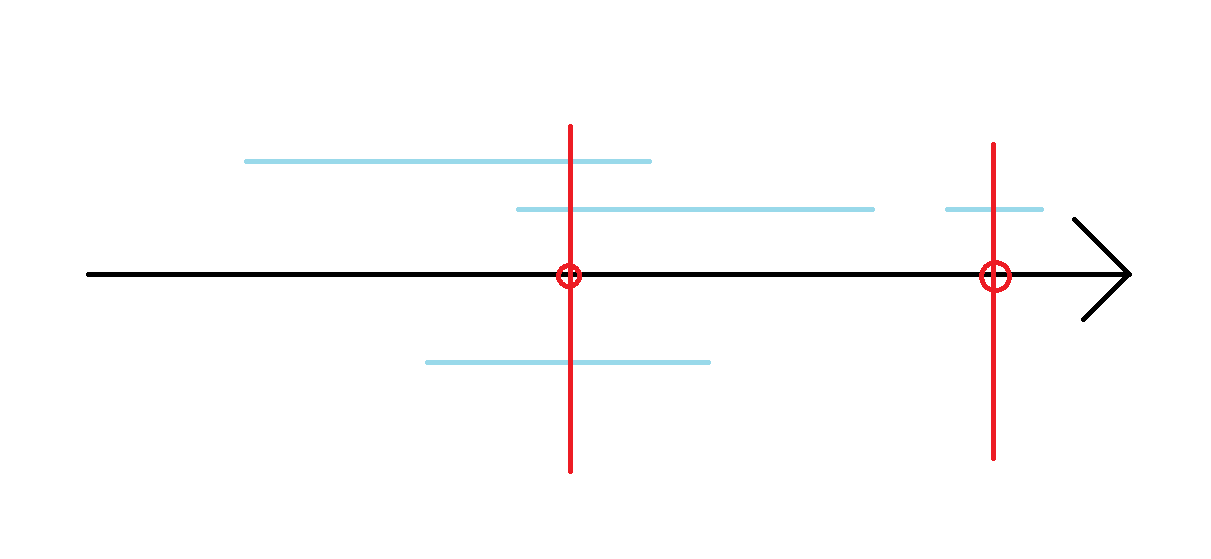
贪心问题去试一些做法:排序,双关键字排序等
尝试没有问题后再去证明
思路:
-
将每个区间按照右端点从小到大进行排序
-
从前往后依次枚举每个区间
① 如果当前区间已经包含点,则直接pass
② 否则,选择当前区间的右端点
证明:
如果能够证明Ans <= cnt,且Ans >= cnt,那么就可以进一步推断出Ans = cnt,从而获得最优解。
- Ans <= cnt
按照我们当前策略来选的话,可以保证每个区间一定会包含一个点,所以当前方案是一组合法方案,最优解是所有合法方案中的最小值。
从而,我们就可以得出第一个结论:最小值一定小于等于一组合法方案,即Ans <= cnt;
2.Ans >= cnt
若要得到第二结论,则要去讨论上文中②情况中的所有点,所有没有被pass的区间是什么情况
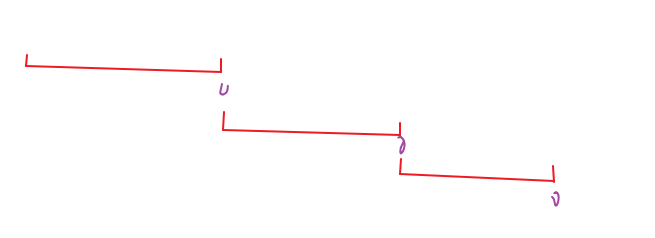
如图,应当是两两互没有任何交集的情况,也就是我们找到了没有任何交集的cnt个区间,只要在这些区间中选点,就可以保证其他区间都有点。我们如果想把这些区间覆盖掉,那么我们至少需要cnt个点。
- 所以,可行方案都大于等于cnt,即Ans >= cnt。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
struct Range{
int l,r;
bool operator< (const Range &w) const{
return r < w.r;
}
}range[N];
int main(){
scanf("%d",&n);
for(int i = 0;i < n;i++){
int l,r;
scanf("%d%d",&l,&r);
range[i] = {l,r};
}
sort(range,range + n);
int res = 0,ed = -2e9;
for(int i = 0;i < n;i++){
if(range[i].l > ed){
res ++;
ed = range[i].r;
}
}
printf("%d\n", res);
return 0;
}
Acwing.908 最大不相交区间数量
类比:
有许多课,他们都有固定的时间,试问最多能上多少节课?
思路:
-
将每个区间按照右端点从小到大进行排序
-
从前往后依次枚举每个区间
① 如果当前区间已经包含点,则直接pass
② 否则,选择当前区间的右端点
选择的端点即为要求的最大不相交的区间数量。
证明:
- Ans >= cnt
按照这种套路选出来的区间相互之间一定没有交集,一定是某一种可行的方案,所以,Ans >= cnt;
- Ans <= cnt
反证法:
假设Ans > cnt,所以我们就可以选择出来比cnt个更多的不相交的区间,我们就至少要选出来cnt + 1个点,才能满足条件。
但这与实际情况不符,我们选出的cnt已经满足条件了,已经可以覆盖区间了,从而证明Ans <= cnt.
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
struct Range{
int l,r;
bool operator< (const Range &w) const{
return r < w.r;
}
}range[N];
int main(){
scanf("%d",&n);
for(int i = 0;i < n;i++){
int l,r;
scanf("%d%d",&l,&r);
range[i] = {l,r};
}
sort(range,range + n);
int res = 0,ed = -2e9;
for(int i = 0;i < n;i++){
if(range[i].l > ed){
res ++;
ed = range[i].r;
}
}
printf("%d\n", res);
return 0;
}
Acwing.906 区间分组
类比:
把每一个区间想象成一个小朋友(bushi),但是呢,有些小朋友之间多少有些过节,他们不能被分到一个组里,得看看怎么分,避免他们打起来
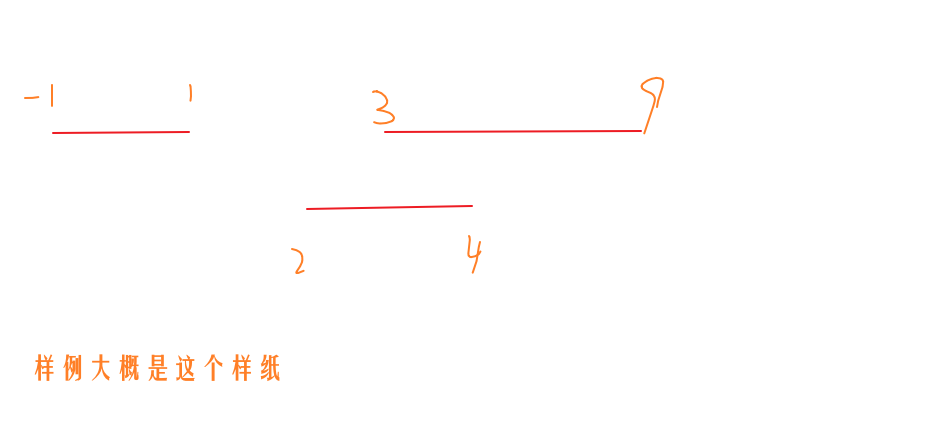
思路:
-
将所有区间按照左端点从小到大进行排序.
-
从前往后处理每个区间.
判断能否将其放到现有的组中 L[i] > Max_r
Ⅰ如果不存在这样的组,则开新组,然后再将其放进去;
Ⅱ如果存在这样的组,将其放进去,并更新当前的Max_r
证明:
Ans是我们最终想要的的答案,cnt是我们这种方案的结果
- Ans <= cnt
因为这种方案一定是一种合法方案,所以cnt必然不小于Ans,即Ans <= cnt;
- Ans >= cnt
如果前面每个组都无法容纳当前这个区间(这个小朋友不太受欢迎),Max_r >= Li
在这种情况下,cnt <= Ans
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
struct Range{
int l,r;
bool operator< (const Range &W)const{
return l < W.l;
}
}range[N];
int main(){
scanf("%d",&n);
for(int i = 0;i < n;i++){
int l,r;
scanf("%d%d",&l,&r);
range[i] = {l,r};
}
sort(range,range + n);
priority_queue<int,vector<int>,greater<int>> heap;
for(int i = 0;i < n;i++){
auto r = range[i];
if(heap.empty() || heap.top() >= r.l) heap.push(r.r);
else {
int t = heap.top();
heap.pop();
heap.push(r.r);
}
}
printf("%d\n",heap.size());
return 0;
}
Acwing.907 区间覆盖
举例:
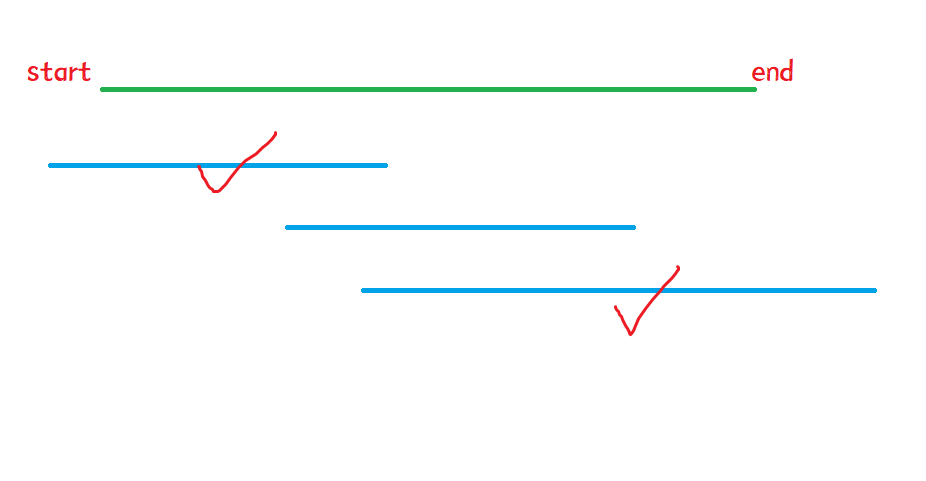
思路:
- 将所有区间按照左端点从小到大排序
- 从前往后依次枚举每个区间,在所有能覆盖start的区间里,选择右端点最大的区间,然后将start更新成右端点的最大值
证明:
【严格的】
先不考虑无解情况
- Ans <= cnt
显而易见,不用证了吧。
Ans是最优解,cnt是当前这种方案的解,必然Ans <= cnt
- Ans >= cnt
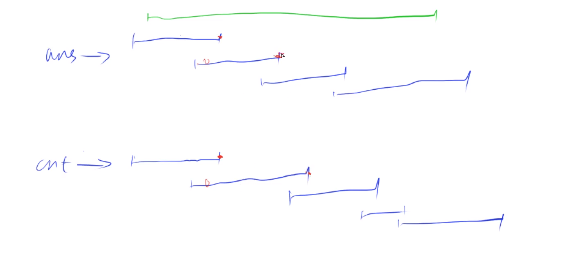
从前往后找到第一个不一样的区间,因为我们的算法排序是找右端点最靠右的区间,所以cnt对应的区间的右端点一定严格大于Ans对应的区间的右端点。
因为下一个区间是与当前区间相互衔接的,所以cnt对应的下一个区间的右端点一定是在Ans对应的下一个区间右端点的右侧。
那么,Ans的当前区间就可以替换为cnt对应的当前区间(反正不亏)
像这样,我们就可以把Ans一步步替换成我们的cnt的解
=>Ans >= cnt
- =>Ans = cnt
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
struct Range{
int l,r;
bool operator< (const Range &W)const{
return l < W.l;
}
}range[N];
int main(){
int st,ed;
scanf("%d%d",&st,&ed);
scanf("%d",&n);
for(int i = 0;i < n;i++){
int l,r;
scanf("%d%d",&l,&r);
range[i] = {l,r};
}
sort(range,range + n);
int res = 0;
bool success = 0;
for(int i = 0;i < n;i++){
int j = i,r = -2e9;
while(j < n && range[j].l <= st){
r = max(r,range[j].r);
j ++;
}
if(r < st){
res = -1;
break;
}
res ++ ;
if(r >= ed){
success = 1;
break;
}
st = r;
i = j - 1;
}
if(!success) res = -1;
printf("%d\n",res);
return 0;
}

