动态规划（DP）——背包问题

（一）原题链接： 01背包问题

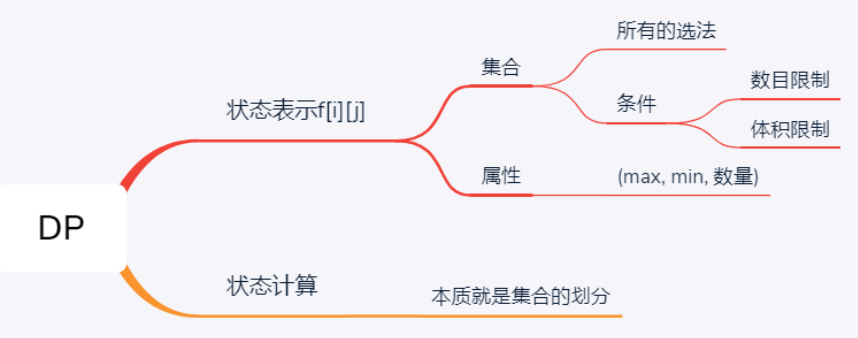
状态表示：$f[i][j]$表示从前$i$个数中选，总体积不超过$j$的最大价值
状态划分：以选或不选第$i$个划分依据，将$f[i][j]$划分为两个集合
状态转移：$f[i][j]=max(f[i-1][j] , f[i-1][j-v[i]]+w[i])$（不选第$i$个，选第$i$个）

#include <iostream>

using namespace std;

const int N = 2020;

int n, m, s;
int f[N][N];
int w[N], v[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i])
            {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }
    }
    cout << f[n][m];
} 

（二）原题链接： 完全背包问题
二维做法：

状态表示：$f[i][j]$表示从前$i$个数中选，总体积不超过$j$的最大价值
状态划分：枚举第$i$个数选取的个数（0个、1个、…若干个)
状态转移：$f[i][j]=max(f[i-1][j] , f[i-1][j-k * v[i]]+k * w[i])$（$k$为第$i$个物品的个数）
但是这样时间复杂度过高，会超时

#include<iostream>

using namespace std;

const int N = 1010;

int f[N][N];
int v[N] , w[N];

int main()
{
    int n,m;
    cin >> n >> m;
    for(int i = 1 ; i <= n ;i ++)
        cin >> v[i] >> w[i];

    for(int i = 1 ; i <= n ; i++)
    for(int j = 0 ; j <= m ; j++)
    {
        for(int k = 0 ; k * v[i] <= j ; k++)枚举第i个物品的数量
            f[i][j] = max(f[i][j] , f[i - 1][j - k * v[i]] + k * w[i]);
    }

    cout << f[n][m] << endl;
} 

一维优化

/*
如何优化掉枚举件数的循环？
f[i][j] = max(f[i-1][j] ,f[i-1][j-2v]+w ,f[i-1][j-3v]+3w,f[i-1][j-4v]+4w.... )
f[i][j -v] = max(        f[i-1][j-2v)   ,f[i-1][j-3v]+2w,f[i-1][j-4v]+3w....)
f[i][j]除第一项的，后面的最大值就等于f[i][j-v]最大值+w
于是f[i][j] = max(f[i][j] , f[i][j-v]+w)

可以发现循环中与i没有关系，于是可以优化掉一维。
本质上是因为，物品无限，所以更新是在已经更新的基础上进行的
*/

#include <iostream>

using namespace std;

const int N = 1010;

int n , m;
int w[N] , v[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1 ; i <= n ; i++)   cin >> v[i] >> w[i];

    for(int i = 1 ; i <= n ; i++)
        for(int j = v[i] ; j <= m ; j++)
             f[j] = max(f[j] , f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

（三）原题链接： 多重背包问题 I

状态表示：$f[i][j]$表示从前$i$个数中选，总体积不超过$j$的最大价值
状态划分：枚举第$i$个数选取的个数（0个、1个、…s[i]个)
状态转移：$f[i][j]=max(f[i-1][j] , f[i-1][j-k * v[i]]+k * w[i])$（$k$为第$i$个物品的个数）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ )
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;
    return 0;
}

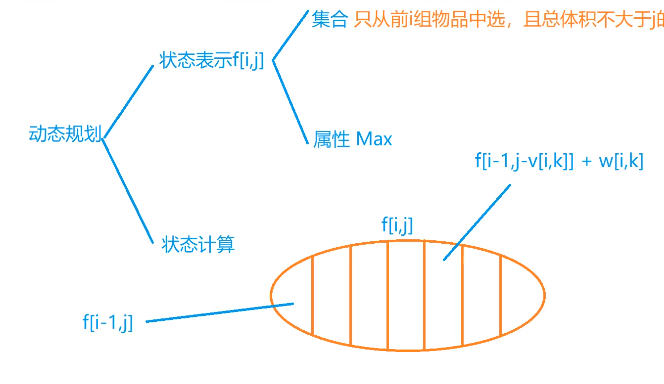
（四）原题链接： 分组背包问题

#include<iostream>

using namespace std;

const int N = 110;

int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i = 1 ; i <= n ; i++)
    {
        cin >> s[i];
        for(int j = 0 ; j < s[i] ; j++)
            cin >> v[i][j] >> w[i][j]; 

    }

    for(int i = 1 ; i <= n ; i++)
        for(int j = 0 ; j <= m ; j++)
        {
            f[i][j] = f[i - 1][j];  //不选
            for(int k = 0 ; k < s[i] ; k++)
                if(j >= v[i][k])     
                    f[i][j]=max(f[i][j] , f[i - 1][j - v[i][k]] + w[i][k]);  
        }

    cout << f[n][m] << endl;
}