scikit-learn：https://scikit-learn.org/stable/

1. 线性回归

• 示例

预测值

$h_{\theta } (x)=\theta _{0}+\theta_{1}x_{1}+\theta _{2}x_{2}$

• x代表样本，里面包含了各种参数，如本示例$x$代表人，$x_{1}$为薪资，$x_{1}$为年龄

一个样本的全部参数经过线性运算后的预测值

$h_{\theta }(x)=\sum_{i=0}^{n} \theta_{i} x_{i} = \theta^{T}x$

当$\theta_{i}$全都确定取值后，根据x1，x2的全部可能取值（全体样本）可构造以下拟合平面

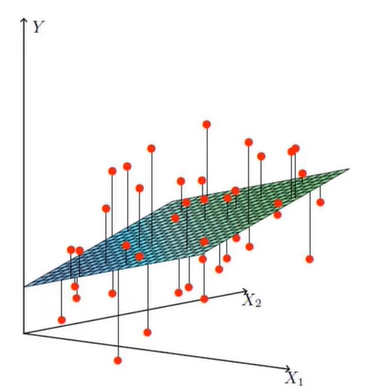
• 其中，$\theta _{0}$用来控制拟合平面移动，系数为1

对于每个样本，真实值=预测值+误差

$y^{(i)}=\theta^{T}x^{(i)}+ \varepsilon ^ {(i)}$(1.1)

• 误差

• $\varepsilon^{(i)}$独立同分布，样本不同决定误差之间独立，实验环境一致决定服从同一个分布

• $\varepsilon^{(i)}$服从正态分布，围绕均值低波动高概率，高波动低概率

由正态分布概率密度公式

$p(\varepsilon^{(i)})=\frac {1}{\sqrt{2 \pi}\sigma}e^{- \frac{{\varepsilon^{(i)}}^{2}}{2\sigma^{2}}}$(1.2)

将(1.1)带入(1.2)

$p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)$

• 最大似然估计

• 标准正态分布误差在0处附近概率最大，所以现在的目标是通过概率计算变量取值，使误差最小，也就是预测值最接近真实值

• 通过联合密度布函数（概率）计算$\theta$的取值，使其满足在总体上$\varepsilon$最接近0

• 又因为样本之间独立同分布，所以联合概率密度函数=每个样本的概率密度函数之积，这就是似然函数

• 接下来就求似然函数的最大值，并求出满足最大值的$\theta$的值

建立似然函数

$L(\theta)=\prod_{i=1}^{m} p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)$

取对数

$\log L(\theta)=\log \prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)$

化简

$\sum_{i=1}^{m} \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)$

$=m \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^{2}} \cdot \frac{1}{2} \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}$

把变量部分单拿出来，定义成一个新函数$J(\theta)$，目标使$J(\theta)$尽可能小

$J(\theta)=\frac{1}{2} \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}$（最小二乘法）

• 梯度下降

目标函数

$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y^{i}-h_{\theta}\left(x^{i}\right)\right)^{2}$（cost function）

• 其中分母的m为样本数量，为了求该$\theta$取值下的代价平均值

• 平方是因为防止累加过程中出现负数影响计算结果，而1/2是为了抵消后续给平方项求导的2（${(x^2)}’ =2x$）

• 平方和/2m操作都是线性的，只影响得数，不影响规模，所以无所谓

批量梯度下降

$\frac{\partial J(\theta)}{\partial \theta_{j}}=-\frac{1}{m} \sum_{i=1}^{m}\left(y^{i}-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i} \quad \theta_{j}^{\prime}=\theta_{j}+\frac{1}{m} \sum_{i=1}^{m}\left(y^{i}-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i}$

• 一次只调整一个参数$\theta_{j}$，每次更新都执行操作:暴力遍历所有样本，取均值，求偏导，更新参数$\theta_{j}$

• 最终能保证对于任意$\theta_{j}$都是最优的，但不能保证$\theta$组在整个参数空间全局最优

• 每次都要遍历所有样本，所以速度很慢

补充偏导数的作用以及取反方向的原因

随机梯度下降

$\theta_{j}^{\prime}=\theta_{j}+\left(y^{i}-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i}$

• 一次只操作一步，但方向不稳定

小批量梯度下降

$\theta_{j}:=\theta_{j}-\alpha \frac{1}{10} \sum_{k=i}^{i+9}\left(h_{\theta}\left(x^{(k)}\right)-y^{(k)}\right) x_{j}^{(k)}$

• $h_{\theta}\left(x^{(k)}\right) \text { 是样本 } k \text { 的预测值， } y^{(k)} \text { 是样本 } k \text { 的实际值， } x_{j}^{(k)} \text { 是样本 } k \text { 的第 } j \text { 个特征值 }$

• 兼顾了速度和准度

• $\alpha$是学习率

• 注意h和y反了，所以-变+了

• code

class LinearRegression:

    def __init__(self,data,labels,polynomial_degree = 0,sinusoid_degree = 0,normalize_data=True):

        (data_processed,
         features_mean,
         features_deviation)  = prepare_for_training(data, polynomial_degree, sinusoid_degree,normalize_data=True)

        self.data = data_processed
        self.labels = labels
        self.features_mean = features_mean
        self.features_deviation = features_deviation
        self.polynomial_degree = polynomial_degree
        self.sinusoid_degree = sinusoid_degree
        self.normalize_data = normalize_data

        num_features = self.data.shape[1]
        self.theta = np.zeros((num_features,1))

    def train(self,alpha,num_iterations = 500): # 迭代次数设置为500

        cost_history = self.gradient_descent(alpha,num_iterations)
        return self.theta,cost_history # 后续可用来可视化展示损失函数

    def gradient_descent(self,alpha,num_iterations):

        cost_history = [] # 损失函数J(θ)
        for _ in range(num_iterations):
            self.gradient_step(alpha)
            cost_history.append(self.cost_function(self.data,self.labels))
        return cost_history


    def gradient_step(self,alpha):

        num_examples = self.data.shape[0]
        prediction = LinearRegression.hypothesis(self.data,self.theta)
        delta = prediction - self.labels
        theta = self.theta
        theta = theta - alpha*(1/num_examples)*(np.dot(delta.T,self.data)).T
        self.theta = theta


    def cost_function(self,data,labels): # 单次的损失值，每次更新θ都记录，反复迭代就成损失函数了(J(θ))

        num_examples = data.shape[0]
        delta = LinearRegression.hypothesis(self.data,self.theta) - labels
        cost = (1/2)*np.dot(delta.T,delta)/num_examples # delta是列向量，所以cost是个1*1的矩阵
        return cost[0][0]

    @staticmethod
    def hypothesis(data,theta):
        predictions = np.dot(data,theta)
        return predictions

两个辅助方法

    def get_cost(self,data,labels):
        data_processed = prepare_for_training(data,
         self.polynomial_degree,
         self.sinusoid_degree,
         self.normalize_data
         )[0]

        return self.cost_function(data_processed,labels)

    def predict(self,data):

        data_processed = prepare_for_training(data,
         self.polynomial_degree,
         self.sinusoid_degree,
         self.normalize_data
         )[0]

        predictions = LinearRegression.hypothesis(data_processed,self.theta)

        return predictions

• 只是把获取损失值和预测值的流程从循环里单拿出来而已，方便后续单独使用

训练数据集并可视化展示

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from linear_regression import LinearRegression

data = pd.read_csv('../../../BaiduNetdiskDownload/data/world-happiness-report-2017.csv')

# 得到训练和测试数据
train_data = data.sample(frac = 0.8)
test_data = data.drop(train_data.index)

input_param_name = 'Economy..GDP.per.Capita.'
output_param_name = 'Happiness.Score'

x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].values

x_test = test_data[input_param_name].values
y_test = test_data[output_param_name].values

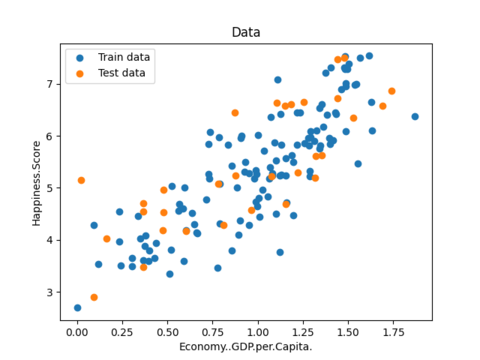
#生成训练集和测试集的散点图
plt.scatter(x_train,y_train,label='Train data')
plt.scatter(x_test,y_test,label='Test data')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Data')
plt.legend()
plt.show()


num_iterations = 500
learning_rate = 0.01

linear_regression = LinearRegression(x_train,y_train)
(theta,cost_history) = linear_regression.train(learning_rate,num_iterations)

print ('开始时的损失：',cost_history[0])
print ('训练后的损失：',cost_history[-1])

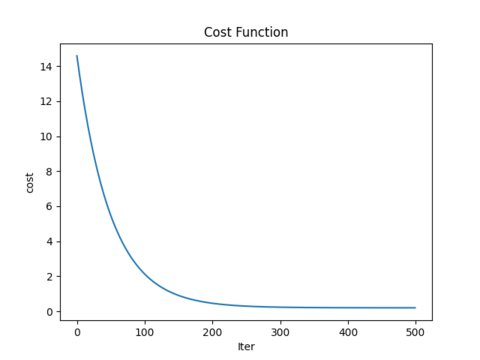
#生成损失函数的折线图
plt.plot(range(num_iterations),cost_history)
plt.xlabel('Iter')
plt.ylabel('cost')
plt.title('Cost Function')
plt.show()


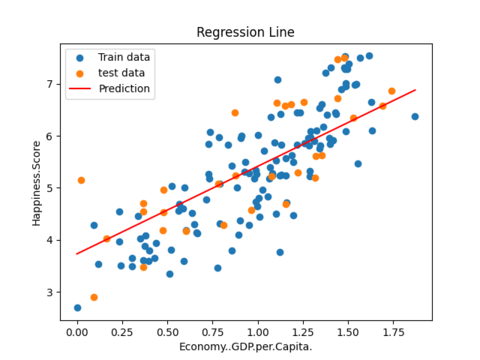
#用迭代后的最终θ，生成回归线
predictions_num = 100
x_predictions = np.linspace(x_train.min(),x_train.max(),predictions_num).reshape(predictions_num,1)
y_predictions = linear_regression.predict(x_predictions)

plt.scatter(x_train,y_train,label='Train data')
plt.scatter(x_test,y_test,label='test data')
plt.plot(x_predictions,y_predictions,'r',label = 'Prediction')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Regression Line')
plt.legend()
plt.show()

• 非线性回归

假设我们想要预测一个人的工资，除了薪资和年龄之外，可能还受到教育程度的影响。用$x_{3}$来表示教育程度，可以构建一个新的非线性回归模型如下

$h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} \sqrt{x_{3}}$

回归线示例（图片与上面公式无关）

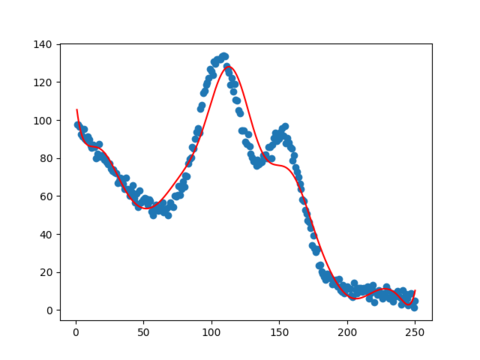
• 从数据集中就可以看出，样本之间存在着非线性的关系，通过调整预测公式来更改回归线形状

• 交互式回归

假设除了房屋的尺寸和年龄之外，还存在着尺寸和年龄之间的交互作用。在这种情况下，我们可以构建一个包含特征乘法关系的非线性回归模型

$h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} x_{1} \cdot x_{2}$