1.完全二叉树的权值 第十届蓝桥杯省赛C++A/B组

读完这个题感觉不难，计算出每行的权值和，然后用两个变量记录下权值和最大值和最小深度:
然后怎么求每行的权值和呢，是有规律的:

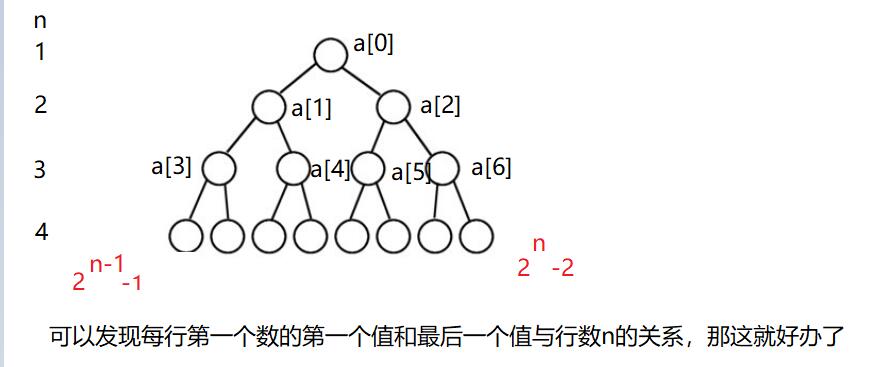
#include<iostream>
#include<math.h>
using namespace std;
int main()
{
    int n,num[100005];
    cin>>n;
    for(int i=0;i<n;++i)
        cin>>num[i];

    int dep=sqrt(n+1);//树的深度
    long long dep_min=1,sum_max=num[0];
    for(int i=1;i<=dep;++i)
    {
        long long sum=0;//权值和
        for(int j=pow(2,i-1)-1;j<=pow(2,i)-2;++j)
            sum+=num[j];
        //cout<<sum<<endl;

        if(sum>sum_max) {
            len_min=i;
            sum_max=sum;
        }
    }
    //cout<<sum_max<<endl;
    cout<<len_min;
}

上边代码运行样例能通过，提交后显示 Segmentation Fault.查看后台数据发现通过了 4/12个数据，当时就看了一下数据范围，感觉应该是求和爆了（但其实是感觉错了）

想了一会不知道应该怎么优化，就去看y总视频了，还没读题呢，就发现了一个致命错误，完全二叉树和满二叉树傻傻分不清…

所以上面代码有问题:即不是满二叉树的情况下，算最后一行权值和的时候会多算，但是也好解决，在for的判断条件加上个j<n就能解决上边这个小问题:

#include<iostream>
#include<math.h>
using namespace std;
int main()
{
    int n,num[100005];
    cin>>n;
    for(int i=0;i<n;++i)
        cin>>num[i];

    int dep=sqrt(n+1);//数的深度
    long long dep_min=1,sum_max=num[0];
    for(int i=1;i<=dep;++i)
    {
        long long sum=0;//权值和
        for(int j=pow(2,i-1)-1;j<=pow(2,i)-2&&j<n;++j)
            sum+=num[j];
        //cout<<sum<<endl;

        if(sum>sum_max) {
            len_min=i;
            sum_max=sum;
        }
    }
    //cout<<sum_max<<endl;
    cout<<len_min;
}

这次提交通过了6/12个数据，还是显示Segmentation Fault错误
想了一会属实想不出来了，就看了看y总的思路:

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long LL;
const int N = 100010;

int n;
int a[N];

int main()
{
    cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i];

    LL maxs = -1e18;
    int depth = 0;

    for(int d=1,i=1;i<=n;i*=2,d++)
    {
        LL s=0;
        for(int j=i;j<i+(1<<d-1)&&j<=n;++j)
            s+=a[j];
        if(s>maxs)
        {
            maxs=s;
            depth = d;
        }
    }
    cout<<depth;
    return 0;
}

y总也是用的long long求和也没爆啊，整体思路也是一样的，唯一不同的就是每行求和的思路不一样.我用了sqrt()和pow()函数，y总没用，那么问题就出在这个地方。难道是这两个函数复杂度太高？
那就先改pow(),之前听说过用快速幂或者位运算求2的n次方，快速幂没看懂，看明白了位运算:
2的n次方用位运算来表示：1 << n;,所以:

#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
int num[100005];
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;++i)
        //cin>>num[i];
        scanf("%d",&num[i]);
    int dep=sqrt(n+1);//数的深度
    long long len_min=1,sum_max=num[0];
    for(int i=1;i<=dep;++i)
    {
        long long sum=0;//权值和
        for(int j=(1<<i-1)-1;j<=(1<<i)-2&&j<n;++j)
            sum+=num[j];
        //cout<<sum<<endl;

        if(sum>sum_max) {
            len_min=i;
            sum_max=sum;
        }
    }
    //cout<<sum_max<<endl;
    cout<<len_min;
}

因为位运算的优先级小于+和-，所以要加括号
这次通过了 11/12个数据。那么就说明sqrt()函数那还有问题
C++——不使用sqrt实现开根号:

#include <iostream>
using namespace std;

float my_sqrt1(int b);

int main() {
    float b;
    cin >> b;
    float re = my_sqrt1(b);
    cout<<re<<endl;
    return 0;
}

float my_sqrt1(int b)
{
    float low = 0, high = b, e = 100, mid;
    while ((e > 1e-6) || (e < -1e-6)) {
        mid = (low + high) / 2;
        e = mid * mid - b;
        if (e > 0)
            high = mid;
        else
            low = mid;
    }
    return mid;
}

在想如何不用sqrt()实现开平方根的时候，突然发现一个问题，由于不是满二叉树，所以不能用n来判断数的深度，因为不是满二叉树，所以树的总节点不可能是2的n次方-1，所以上边思路不对.
那为什么又能通过11/12个样例呢?
做了个实验，输入:
6
1 6 5 4 3 20
输出的还是2，那这就能说明问题了，说明过的那11个数据，权值和最大的都不在最后一行，第12个数据的最大权值和在最后一行…