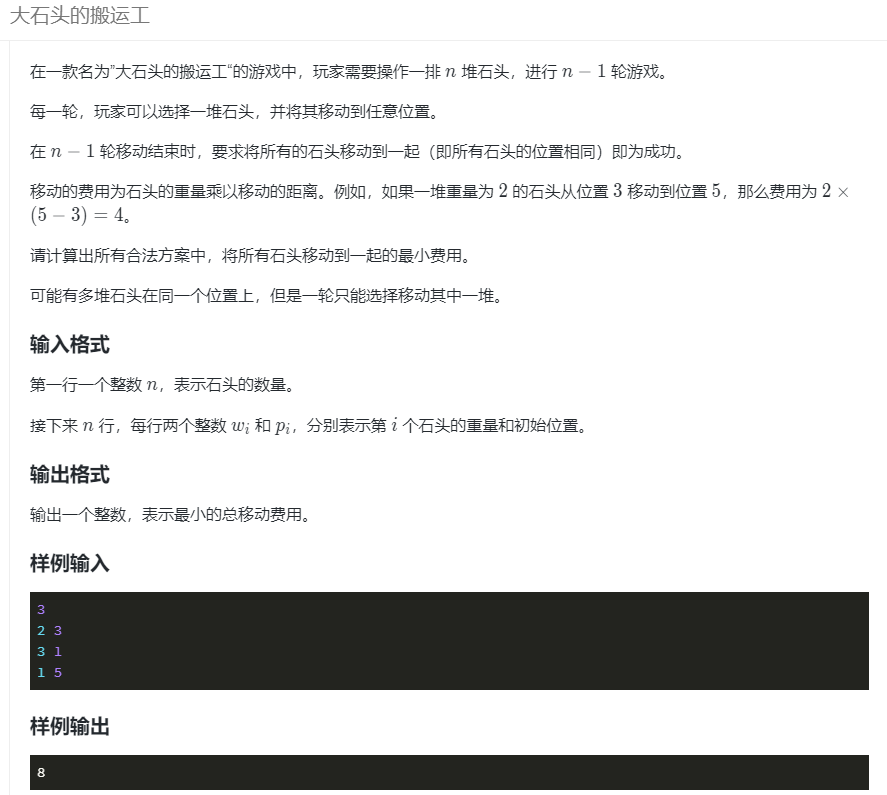
前缀和的应用一

import java.util.*;

public class Main{

    public static class node implements Comparable<node>{
        int x,y;
        public node(int x, int y){
            this.x = x;
            this.y = y;
        }

        @Override
        public int compareTo(node o1){
            return this.y - o1.y;
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n  = sc.nextInt();
        node [] a = new node[n + 2];
        //注意这里a[0]和a[n + 1]是没有值
        //但是我们却用到了，如果不new的话，就会报空指针的错误
        a[0] = new node(0, 0);
        a[n + 1] = new node(0, 0);

        //读入
        for(int i = 1; i <= n; i ++) a[i] = new node(sc.nextInt(), sc.nextInt());
        long [] pre = new long[n + 2];
        long [] nex = new long[n + 2];
        Arrays.sort(a, 1, n + 1);
        long s = 0;
        //直接存的费用 = 距离乘重量
        //前缀和 
        //pre[i]表示将前i - 1堆都搬到第i堆的花费
        for(int i = 1; i <= n; i ++)
        {
            pre[i] = pre[i - 1];
            pre[i] += (a[i].y - a[i - 1].y) * s;
            s += a[i].x;
        }

        s = 0;
        //后缀和
        //nex[i]表示将n、n - 1、n - 2...i + 1堆搬到第i堆的花费
        for(int i = n; i >= 1; i --)
        {
            nex[i] = nex[i + 1];
            nex[i] += (a[i + 1].y - a[i].y) * s;
            s += a[i].x;
        }

        long ans = (long) 1e18;

        for(int i = 1; i <= n; i ++)
        {
            ans = Math.min(ans, pre[i] + nex[i]);
        }
        System.out.println(ans);



    }
}

前缀和应用二

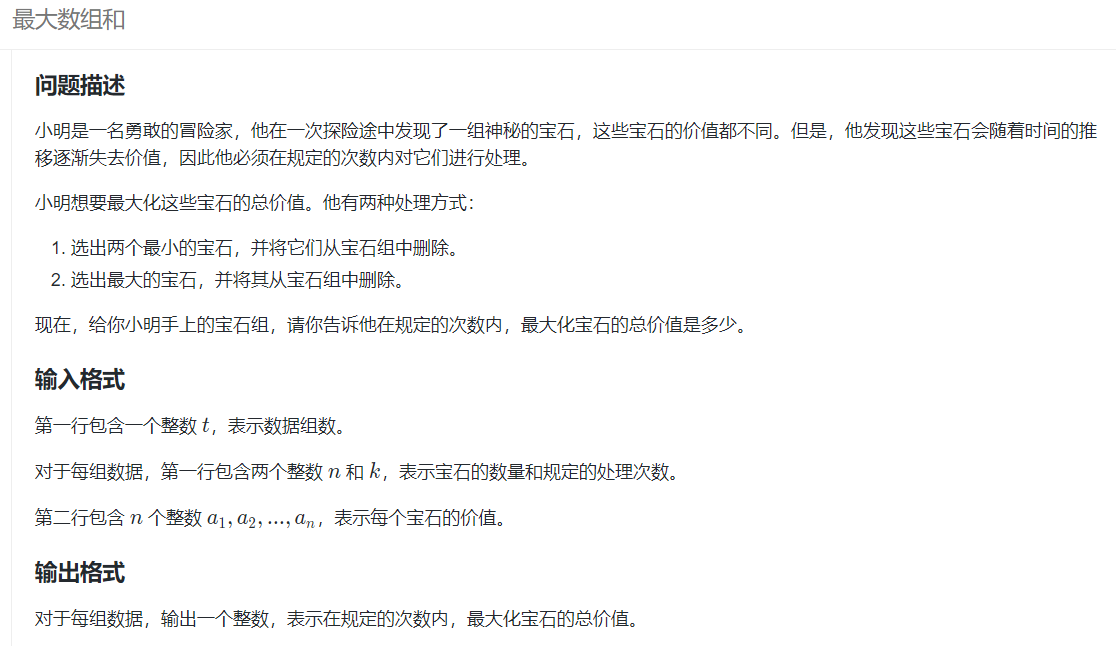
分析与思路

一开始的想法是去进行简单的模拟

我们刚开始的猜测是通过每次比较最小的两个数和最大的数，谁小我们就删除谁

但是这种想法是贪心的，只是根据当前局部最优解而做出判断

比如样例：
输入
6 2
15 22 12 10 13 11
输出
46

当数据sort后 10 11 12 13 15 22
按照原先的想法我们应该先删除10和11，在删除22，但是这样得到的res = 40是小于正确答案46的

正确的做法应该是先删除22 再删除15 得到最终res = 46

我们没有办法证明贪心是正确的，根据样例可知，我们这种实现方式是错误的！

CODE

import java.util.Arrays;
import java.util.Scanner;

public class Main{
    static int N = 2_000_10;
    static long [] a = new long [N];
    static long [] s = new long [N]; 
    static int n, T, k;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        T = sc.nextInt();
        while(T -- > 0){
            n = sc.nextInt();
            k = sc.nextInt();
            long sum = 0;
            for(int i = 1; i <= n; i ++) {
                a[i] = sc.nextLong();
                sum += a[i];
            }
            Arrays.sort(a, 1 , n + 1);
            for(int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i];

            long res = 0;

            //用x表示删除两个最小数的次数
            //x的取值范围是[0, k] 那么删除最大数字次数y就是k - t
            for(int x = 0; x <= k; x ++)
            {
                int y = k - x; //删除最大数字的次数
                //开始操作了

                //删除x次两个最小的数字
                //删除1次，减去[1,2]
                //删除2次，减去[1,4]
                //删除k次，减去[1, 2 * k]
                long t1 = 0; //如果删除最小的两个数的次数是0的话，也不需要减了
                if(x > 0) t1 = s[2 * x] - s[0];

                //删除1个最大数字就是s[n] - s[n - 1]
                //删除2个最大数字就是s[n] - s[n - 2]
                //删除k个最大数字就是s[n] - s[n - k]
                long t2 = 0; //如果不需要删除最大数字
                if(y > 0) t2 = s[n] - s[n - y];

                //求最大值
                res = Math.max(res, sum - t1 - t2);
            }

            System.out.println(res);

        }

    }
}

前缀和应用三 (和前缀和有个几把关系啊，感觉考的是数学知识和单调栈的性质)

根本想不到这个做法

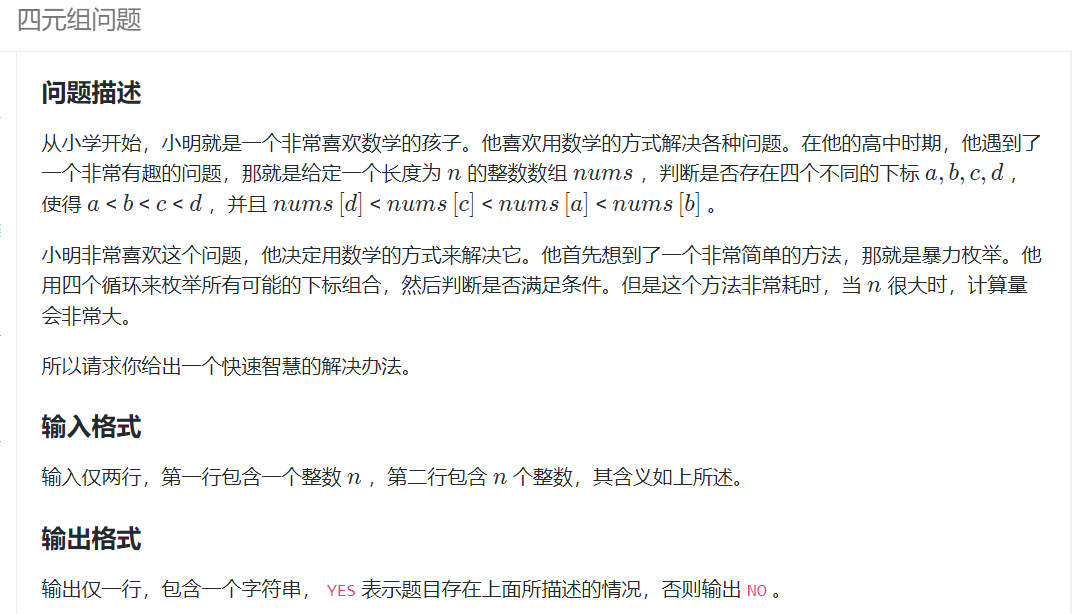
分析与思路

确定三元组，来去找d,预处理出来mins[i]数组，表示第i个元素右边最小的值，如果最小的元素mins[i]都不满足mins[i] < nums[c]的话，那么其他元素必然也不会满足。

mins[i]数组表示第i个数右边的最小的数字（当然不包含第i个数）
因此可以推导如下：
（1）那么mins[i]数组可以预处理出来，mins[i] = Math.min(mins[i - 1], a[i - 1])

（2）剩下需要考虑nums[c] < nums[a] < nums[b]
先去找满足条件的nums[a] < nums[b]
这样我们只需要最后去找b后面有没有满足条件的c即可

（3）找nums[a] < nums[b]用到了单调栈

栈是单调递减的

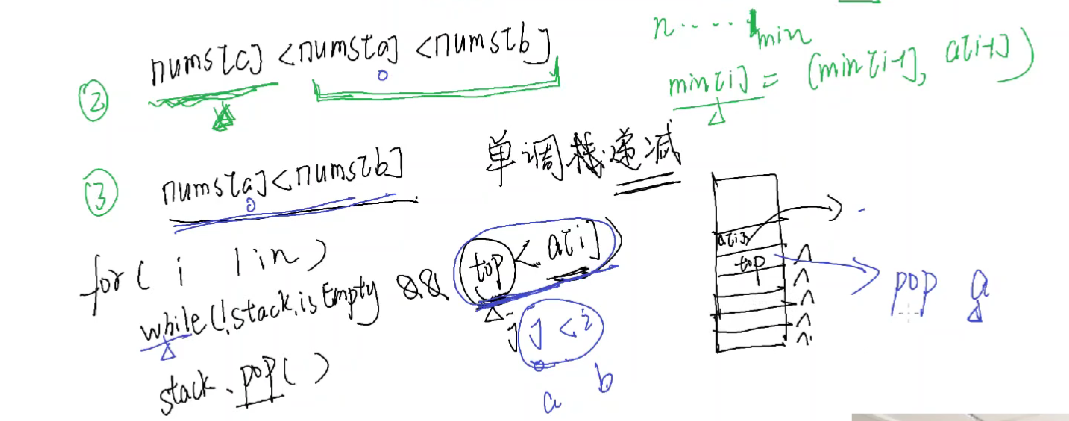
新加入一个ai，这个a[i]就相当于是b，a[i] > stack.top()

因为栈是递减的，所以栈顶应该弹出，所以这里的stack.top()相当于是a

a更大一点是更优的，因为我们后续还要选择c，我们希望后面c可选的值更多，因此这样c能够存在的概率是更大的

for循环遍历数组
  while(!stack.isEmpty && top < a[i])
  {
      k = max(stack.pop(), k); //弹出来的值相当于是a
      //这里的k就是a，越大越好
  }
  //但是注意要先找到a,k被赋值了，才能进行下面的判断
  //因此我们可以先给k赋一个没出现的值
  //然后当k不等于那个没有出现过的值的话，才满足判断
  只要a[i + 1] < k的话
  c也找到了

  这样a、b、c都找到了
  如何找d，只需要判断a[i + 1]后面有比a[i + 1]还小的数字即可
  if(mins[i + 1] < a[i + 1]) cout << "YES";
  else cout << "NO";

CODE

import java.util.Arrays;
import java.util.Scanner;
import java.util.Stack;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int [] a = new int [n + 1];
        int [] mins = new int [n + 1];
        Arrays.fill(mins, Integer.MAX_VALUE);

        for(int i = 1; i <= n; i ++) a[i] = sc.nextInt();

        //预处理mins[]数组
        for(int i = n - 1; i >= 1; i --)
        {
            mins[i] = Math.min(mins[i + 1], a[i + 1]);
        }

        int k = Integer.MIN_VALUE;
        Stack<Integer> stack = new Stack<>();
        for(int i = 1; i <= n; i ++)
        {
            //k就是代表a的值
            //k > a[i], a[i]代表num[c]的值
            //mins[i]表示a[i]右边最小的值
            //如果mins[i] < a[i] 代表 num[c] > num[d]
            if(k > a[i] && mins[i] < a[i]){
                System.out.println("YES");
                return; //java也能return啊。。。
                //也对啊，主函数是void main
                //而c语言则是int main -> return 0
            }

            //这里的ai就是b了
            //a[i] 大于了当前栈顶也就是a[i]之前的元素b
            //找到后，将栈顶元素弹出，记录a的值，看看i ++后面是不是c和d满足要求了
            //否则，这里成为新的栈顶
            while(stack.isEmpty() == false && stack.peek() < a[i]){
                k = Math.max(k, stack.pop());
            }

            stack.push(a[i]);
        }

        System.out.println("NO");

    }
}