二分模板（两个模板的使用场景以及mid的更新方式）

如果遇到的问题是可以通过某种性质，把讨论对象的范围分成多份的话，即A部分具有某种性质B部分不具有，就可以通过二分来找到这边界点

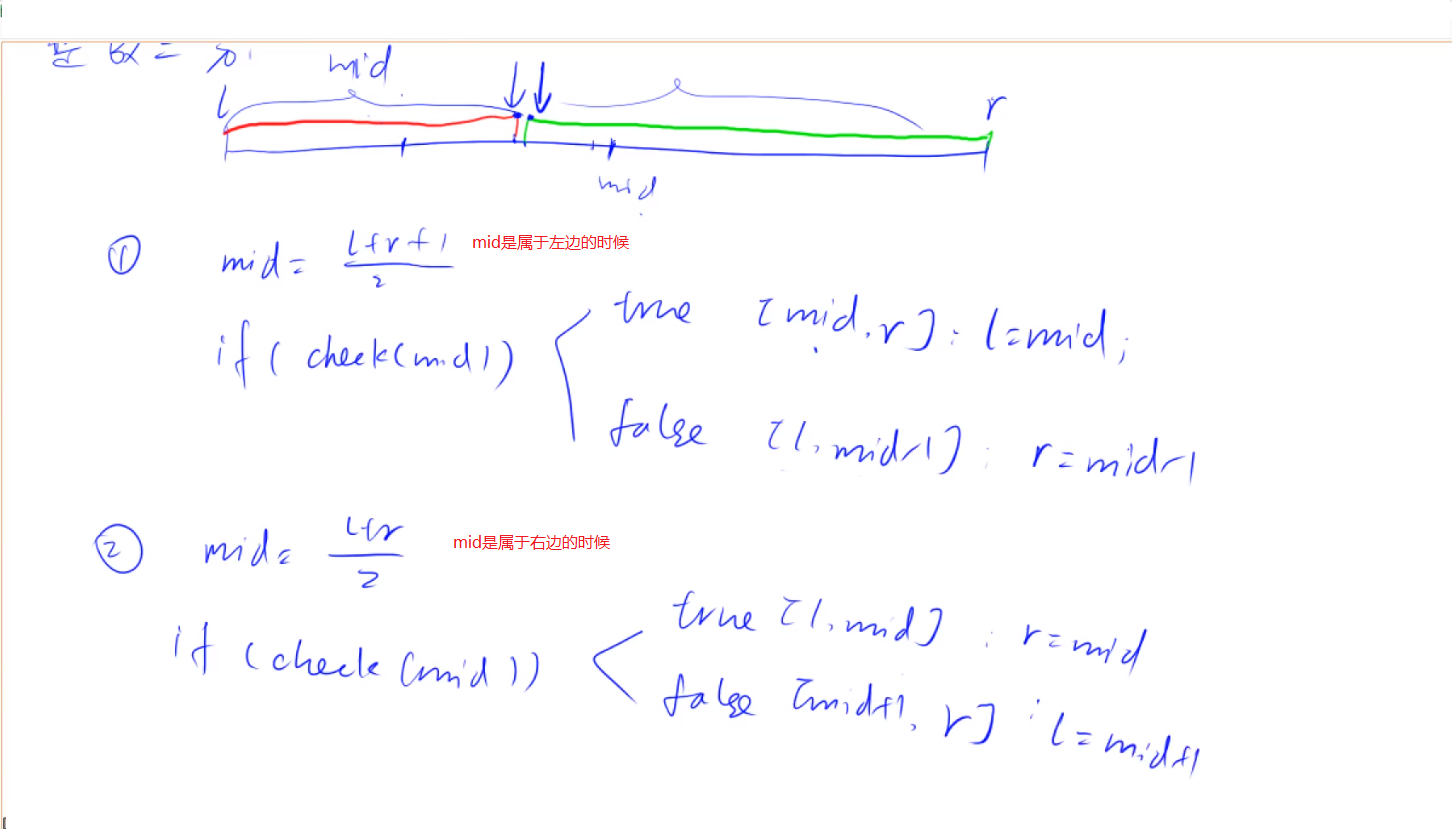
如果我们要划分出来的是绿色的边界

• mid 是绿 [L, R] -> [L, mid]， mid 是红 [L, R] -> [mid + 1, R];

• 如果mid落在绿色的区域内的时候，我们就可以发现R可以更新成mid

• 并且因为都是绿色区域的点，所以可能出现mid就是边界的情况所以不用减一

• 相对的如果出现在红色区域，那么很确定该点不可能是绿色的边界点，可以大胆的加一

int bsearch(int x){
    int l = 0, r = nums.siez() -1;
    while(l < r){
        int mid = l + r >> 1;
        if(check(mid)) return r = mid;
        else l = mid + 1; 
    }
}

如果我们要划分出来的是红色的边界

• mid 是红 [L, R] -> [mid, r]， mid 绿 [L, R] -> [L, mid - 1];

• 如果mid落在红色的区域内的时候，我们就可以发现l可以更新成mid

• 并且因为都是红色区域的点，所以可能出现mid就是边界的情况所以不用加一

• 相对的如果出现在绿色区域，那么很确定该点不可能是红色的边界点，可以大胆的减一

• 注意，这个模板的计算mid的时候要加一

int bserach(int x){
    int l = 0, int r = nums.size() - 1;
    while(l < r){
        int mid = l + r + 1>> 1;
        if(check(mid)) l = mid;
        else r = mid -1
    }
}