线性拟合

1 - 什么是线性拟合

举个直观的例子，在平面直角坐标系中已知一系列点，

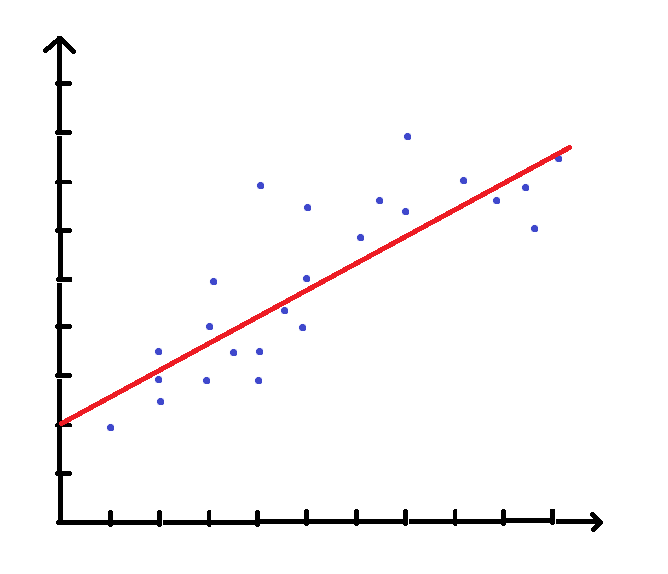
尽管略有偏差，但是凭借人类的直觉，

我们不难看出这些点大都分布在直线 $y=\frac{1}{2}x+2$ 两侧。

线性拟合要做的就是这样一件事，

——画“线”来拟合点分布的规律。

在这个例子里，自变量和因变量各有一个，

类似的例子还有：

• 自变量 $x$ 为温度，因变量 $y$ 为体温计的水银柱高度
• 自变量 $x$ 为大楼层数，因变量 $y$ 为该楼高度
• 自变量 $x$ 为赛道长度，因变量 $y$ 为运动员耗时
• …………

但更多时候，自变量和因变量可以是多个，

比如：

• 自变量为 $x_1$ ， $x_2$ ，因变量为 $y=1.2x_1+0.8x_2$
• 自变量为天数，因变量为甲队施工进度和乙队施工进度
• 自变量为试卷题量、难度，因变量为成绩达标的学生数量、成绩优秀的学生数量
• …………

不过，多个因变量的情况和一个因变量的情况其实是一样的，

因为它可以被拆解为多个单因变量的问题。

所以，我们知道了一系列数据：

自变量 ---------> 因变量
$x^{(1)}_{1}$ $x^{(1)}_{2}$ … $x^{(1)}_{m}$ ----> $y^{(1)}$
$x^{(2)}_{1}$ $x^{(2)}_{2}$ … $x^{(2)}_{m}$ ----> $y^{(2)}$
…………
$x^{(n)}_{1}$ $x^{(n)}_{2}$ … $x^{(n)}_{m}$ ----> $y^{(n)}$

（第 $i$ 行的自变量记为 $x^{(i)}$ ， 第 $i$ 行第 $j$ 个自变量记为 $x^{(i)}_{j}$）

希望找出一个函数

$f_{K}(x)=k_{0}+k_{1}x_1+k_{2}x_2+…+k_{m}x_m$ ，

（$k_0$ ， $k_1$ ， $k_2$ … $k_m$ 记为 $K$）

使得 $J(K)=\frac{1}{2n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})^2}$ 最小，

乘 $\frac{1}{2n}$ 是为了后面计算方便。

可以发现 $J(K)$ 越小，我们预测的值 $f_{K}(x)$ 总体上就越接近 $y$ ，

正合我们的意思。

2 - 如何做线性拟合

(1) 梯度下降法

现在问题被转化为了 找到合适的 $K$ 使得 $J(K)$ 最小

用推公式的方法貌似太难了，所以我们用一种直观的思维考虑。

想象一下：

你身处群山之中，

各个系数 $k_0, k_1…$ ，就是经度、纬度……

某个经纬度上的山高，就是这些系数对应的 $J(K)$ ，

你一开始在某个位置，想用尽量少的步数走到低处，

也就是用尽量少的步数走到使 $J(K)$ 最小的 $K$ 处。

每一步该怎么走？从 方向 和 步长 两个方面来看。

尽量用最少的步数，意味着每次都要往最“陡”的方向前进，

而“最陡的方向”，又等于“东西方向上最陡的方向” + “南北方向上最陡的方向”，

或者说，斜着走一步可以等效于东西走一步再南北走一步。

至于步长，越陡迈步越大就行了。

（学过微积分的大佬，可能已经知道了，我们就是要往目前位置的 $J(K)$ 关于各个系数的偏导的反方向前进）

但对于微积分没有系统学过的人（包括我），直接把伪代码给出来吧，

向最陡的方向走一步意味着：

$j$ 从 $1$ 到 $m$ 枚举 $k_{j}$

$k_{j}=k_{j}- \alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)}) x^{(i)}_{j}}$

//这里 $\alpha$ 叫做学习率，
//用较小的学习率，就好像小心翼翼地试探，拟合结果比较精确
//用较大的学习率，就好像大步迈开向前进，拟合结果比较粗糙

$k_0$ 比较特殊， $k_{0}=k_{0}- \alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)}) \times 1}$

所以我们也可以认为有一个 $x^{(i)}_{0}$ 始终等于 $1$

这种方法称为 梯度下降法 ，

梯度就是前文所说的最“陡”的方向。

总流程如下：

1. 初始化学习率 $\alpha$ ，大一些，
2. 初始化位置 $K$ ，一般为全 $0$ ，
3. 持续往最“陡”的方向前进，直到停在原地或者走了太多步，
4. 如果是走了太多步，那么适当减小学习率 $\alpha$ ，回到步骤 $1$ 再试一次，
5. 否则训练完成，你可以输入自变量，模型就会把它代入 $f_{K}$，帮你估计因变量的值了。

(2) 学习率与结束边界

前文梯度下降法的第 $3$ 步，我们要判断 $K$ 是否停在了原地，

方法是设定一个很小的结束边界值 $eps$ ，如果 $\forall \, 0 \leq i \leq m, \, |k_{i \, now}-k_{i \, past}|<eps$ ，

那么就认为 $K$ 稳定了。

但除了停在原地，还有一种走了太多步的情况。

由于 $alpha$ 不合适造成这种情况的原因有两种，如图：

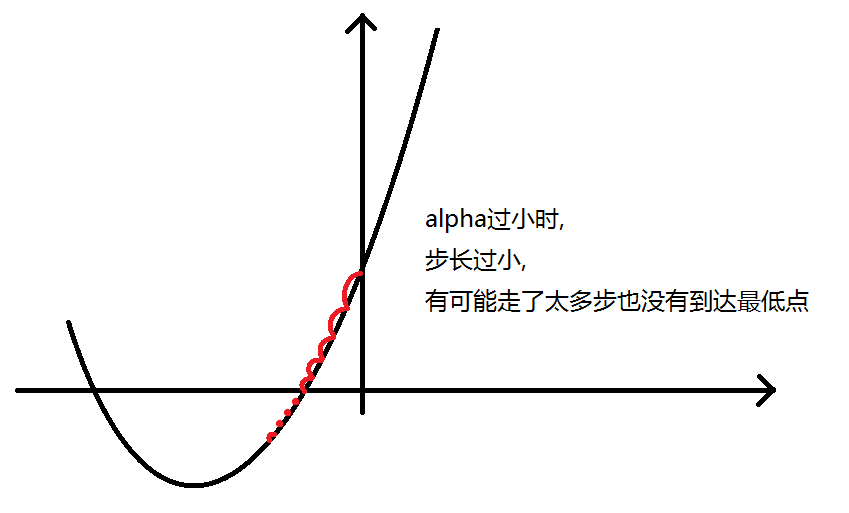
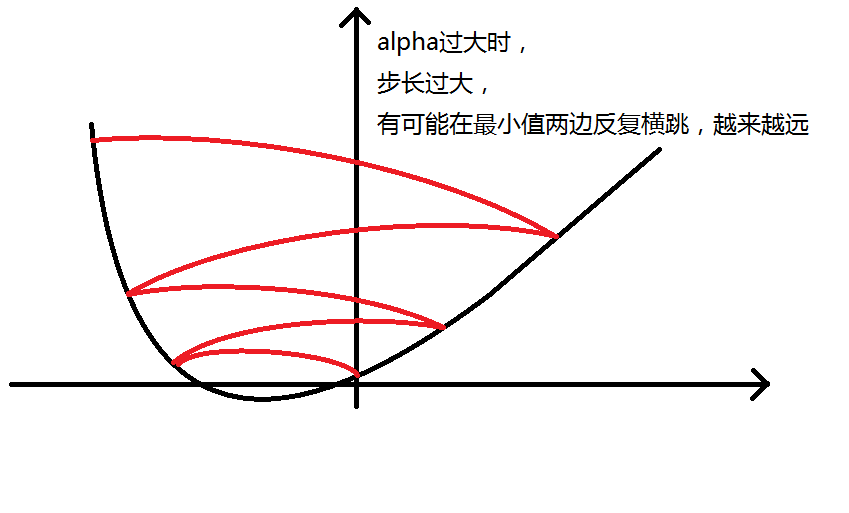
正因为如此，我们在梯度下降时要尝试不同的 $\alpha$ 。

注意 $eps$ 的值也要合适，否则可能出现这样的错误：

1. 相对于 $alpha$ ， $eps$ 如果过大，条件太宽松，可能导致程序误判 $K$ 已经停在原地，过早停止迭代
2. 相对于 $alpha$ ， $eps$ 如果过小，条件太苛刻，可能导致程序迭代太久，这种情况要与上文的 $alpha$ 过大分清

(3) 非线性拟合

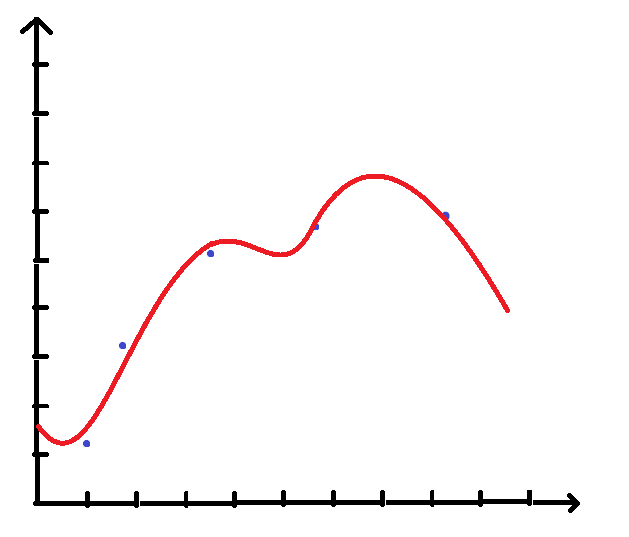
回到开头的图，有人可能会认为用一条曲线，拟合效果更佳：

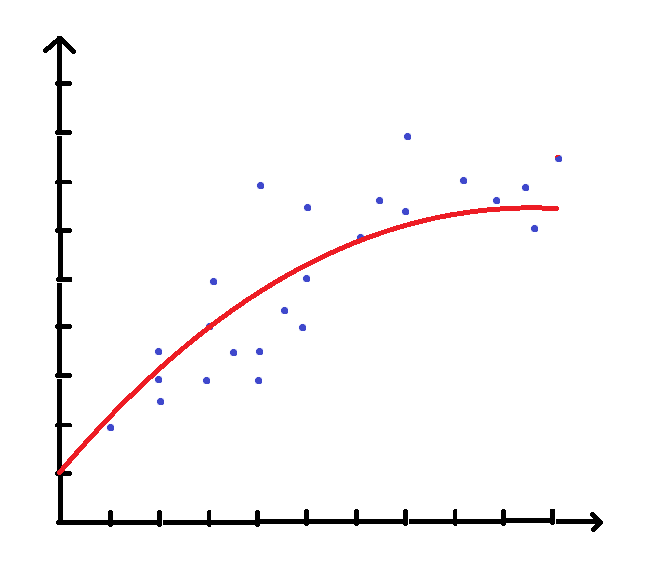
实现非线性拟合比较简单，

只需要加入一些非线性的自变量，

比如原自变量有 $x_1, x_2$ ，

我们可以添加诸如 $x^{2}_{1}$ ， $x^{2}_{2}$ ， $x_{1}x_{2}$ 甚至 $\sin{x_1}$ ， $\cos{x_2}$这样的项，

这样就实现了用线性拟合的方法解决非线性拟合问题。

(4) 正则化

进行非线性拟合时，有可能出现这样一种情况：

这个模型在训练集上表现非常好，

但很明显，它并不能反应数据分布的规律，

这种情况被称为 过拟合 。

究其原因，是因为高次项的系数太大，对模型的影响太大。

于是，我们便需要一种优化方法，约束高次项的系数，

这种方法称为 正则化 。

正则化有两种： $L1$ 和 $L2$ 正则化，

这里讲更常用的 $L2$ 正则化。

对 $J(K)$ 进行修改：

$J(K)=\frac{1}{2n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})^2}+\frac{\lambda}{2n} \sum_{i=1}^{m}{k^{2}_{i}}$

之前讲的伪代码也要相应地修改：

$k_{j}=(1-\alpha \frac{\lambda}{n}) k_{j}-\alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)}) x^{(i)}_{j}}$
但 $k_{0}=k_{0}-\alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)}) \times 1}$ 不变

每次更新 $K$ 时先将非常数项的系数缩小，再加上偏移量，

就可以有效地防止过拟合。

(5) 数据缩放

一些自变量、因变量的范围很大（如二次、三次项）或很小，

先对它们进行缩放调整，

再进行训练和使用。

通俗了说就是防止爆double

3 - C++代码实现

//简单起见，因变量只有一个，只能添加原自变量的指数作为新自变量，用于非线性拟合
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <fstream>

using namespace std;

const int N = 100010, M = 110;
const double eps = 1e-4;
int n, m, k;
double alpha = 1.0, lambda = 5.0;
bool reg = true;

struct Data {
    double x[M], y;
} datas[N];

struct Weight {
    double theta[M];
} result, tmp;

struct Ratio {
    double x[M], y;
} ratio;

double h(double x[]) {
    double res = 0.0;
    for (int i = 0; i <= m; i ++) res += result.theta[i] * x[i];
    return res;
}

bool GDA() {
    memset(result.theta, 0, sizeof(result.theta));

    int limit = 100000, cnt = 0;
    while (cnt < limit) {
        for (int j = 0; j <= m; j ++) {
            tmp.theta[j] = 0.0;
            for (int i = 1; i <= n; i ++)
                tmp.theta[j] += (h(datas[i].x) - datas[i].y) * datas[i].x[j] / n * alpha;
            tmp.theta[j] += (j > 0) * reg * alpha * lambda / n * result.theta[j];
        }

        bool flag = true;
        for (int j = 0; j <= m; j ++) flag &= (fabs(tmp.theta[j]) < eps);
        if (flag) return true;

        for (int j = 0; j <= m; j ++) result.theta[j] -= tmp.theta[j];
        cnt ++;

//      for (int i = 0; i <= m; i ++) printf("%.1lf ", result.theta[i]);
//      puts("");
        if (cnt % (limit / 10) == 0) printf("%d %\n", cnt / (limit / 100));
    }

    return false;
}

int main() {
    printf("数据组数："); scanf("%d", &n);
    printf("特征个数："); scanf("%d", &m);
    printf("多项式次数："); scanf("%d", &k);
    m *= k;

    printf("输入缩放倍率：\n");
    printf("常数项缩放倍率："); scanf("%lf", &ratio.x[0]);
    for (int i = 1, j = 1; i <= m; i += k, j ++)
        for (int u = 0; u < k; u ++) {
            printf("特征%d，%d次幂缩放倍率：", j, u + 1);
            scanf("%lf", &ratio.x[i + u]);
        }
    printf("输出缩放倍率: "); scanf("%lf", &ratio.y);
    printf("是否正则化："); scanf("%d", &reg);
    if (reg) printf("正则化参数："), scanf("%lf", &lambda);

    ifstream in("这里填输入文件的位置，如C:\\Users\\xxxxx\\Desktop\\datas.txt，注意用双斜杠");
    for (int i = 1; i <= n; i ++) {
        datas[i].x[0] = 1.0 * ratio.x[0];
        for (int j = 1; j <= m; j += k) {
            double x;
            in >> x;

            double val = 1.0;
            for (int u = 0; u < k; u ++) {
                val *= x;
                datas[i].x[j + u] = val * ratio.x[j + u];
            }
        }
        in >> datas[i].y;
        datas[i].y *= ratio.y;
    }

    while (alpha >= 0.001) {
        printf("alpha = %.3lf\n", alpha);
        bool flag = GDA();
        if (flag) break;
        else alpha /= 10;
    }

    printf("[%.3lf]\n", result.theta[0] * ratio.x[0] / ratio.y);
    for (int i = 1, j = 1; i <= m; i += k, j ++)
    {
        putchar('[');
        for (int u = 0; u < k; u ++)
        {
            printf("%.3lf", result.theta[i + u] * ratio.x[i + u] / ratio.y, j, u + 1);
            if (u < k - 1) printf(", ");
        }
        puts("]");
    }
    puts("");

    double query[M];
    while (true) {
        query[0] = 1.0;
        for (int i = 1; i <= m; i += k) {
            double x;
            scanf("%lf", &x);

            double val = 1.0;
            for (int u = 0; u < k; u ++) {
                val *= x;
                query[i + u] = val * ratio.x[i + u];
            }
        }
        double res = h(query) / ratio.y;
        printf("%.3lf\n", res);
    }

    return 0;
}

其他

正则化后 伪代码 的证明：

对于 $0<j \leq m$
$$ \begin{align} k_{j} &=k_{j}-\alpha \frac{\partial}{\partial k_{j}} J(K) \\\\ &=k_{j}-\alpha \frac{\partial}{\partial k_{j}} (\frac{1}{2n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})^2}+\frac{\lambda}{2n} \sum_{i=1}^{m}{k^{2}_{i}}) \\\\ &=k_{j}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{2n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})^2}-\frac{\partial}{\partial k_{j}} \frac{\lambda}{2n} \sum_{i=1}^{m}{k^{2}_{i}} \\\\ &=k_{j}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{2n} \sum_{i=1}^{n}{f^{2}_{K}(x^{(i)})}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{2n} \sum_{i=1}^{n} {2f_{K}(x^{(i)})y^{(i)}}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{2n} \sum_{i=1}^{n}{y^{(i)2}}-\frac{\partial}{\partial k_{j}} \frac{\lambda}{2n} \sum_{i=1}^{m}{k^{2}_{i}} \\\\ &=k_{j}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{n} \sum_{i=1}^{n}{( \sum_{t=0}^{m}{k_{t}k_{j}x^{(i)}_{t}x^{(i)}_{j}}-k^{2}_{j}x^{(i)}_{j})}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{n} \sum_{i=1}^{n} {f_{K}(x^{(i)})y^{(i)}}-\alpha \frac{\partial}{\partial k_{j}} \frac{1}{2n} \sum_{i=1}^{n}{y^{(i)2}}-\frac{\partial}{\partial k_{j}} \frac{\lambda}{2n} \sum_{i=1}^{m}{k^{2}_{i}} \\\\ &=k_{j}-\alpha \frac{1}{n} \sum_{i=1}^{n}{(\sum_{t=0}^{m}{k_{t}x^{(i)}_{t}})x^{(i)}_{j}}-\alpha \frac{1}{n} \sum_{i=1}^{n}{y^{(i)}x^{(i)}_{j}}-\alpha \frac{\lambda}{n} k_{i} \\\\ &=k_{j}-\alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})x^{(i)}_{j}}-\alpha \frac{\lambda}{n} k_{i} \\\\ &=(1-\alpha \frac{\lambda}{n}) k_{i} -\alpha \frac{1}{n} \sum_{i=1}^{n}{(f_{K}(x^{(i)})-y^{(i)})x^{(i)}_{j}} \end{align} $$