一维前缀和

在了解二维前缀和之前，我们首先需要了解一下什么是前缀和。

如果我给你一串长度为n的数列a1,a2,a3......an,再给出m个询问，每次询问给出L，R两个数，要求给出区间[L,R]里的数的和，你会怎么做，若是没有了解过前缀和的人看到这道题的想法可能是对于m次询问，我每次都遍历一遍它给的区间，计算出答案，这样子的方法固然没错，但是其时间复杂度达到了O(n*m)，如果数据量稍微大一点就有可能超时，而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n+m),大大节省了运算时间。至于怎么用，请看下面一小段代码
题目来源

for(int i=1;i<=n;i++)
   a[i]+=a[i-1];

前缀和顾名思义就是前面i个数的总和。数组a在经过这样的操作之后，对于每次的询问，我们只需要计算a[R]-a[L-1]就能得到我们想要的答案了，是不是很简单呢。

一维差分

在知道了最简单的前缀和之后，我们再来了解一下什么是差分。

给你一串长度为n的数列a1,a2,a3......an，要求对a[L]~a[R]进行m次操作：

操作一：将a[L]~a[R]内的元素都加上c

操作二：将a[L]~a[R]内的元素都减去c

最后再给出一个询问求a[L]-a[R]内的元素之和？

你会怎么做呢？你可能会想，我对于m次操作每次都遍历一遍a[L]~a[R],给区间里的数都加上c或减去c，最后再求一次前缀和就行了。没错，这样子确实也能得出正确答案，但时间复杂度却高达O(M*n)，对于1<=n,m<=1e5这个数据范围来说直接就GG了，所以说这个方法不可行。既然这样不行的话，那我们要怎么做才能快速的得到正确答案呢？是的，这个时候我们的差分就该派上用场了，我们新开一个数组b，储存每一次的修改操作，最后求前缀和的时候统计一下就能快速的得到正确答案了，详细请看下面代码。
题目来源

#include<iostream>
using namespace std;
const int N=100010;
int a[N],s[N];
int n,m;
void insert(int l,int r,int c){
    s[l]+=c;
    s[r+1]-=c;
}
int main()
{
   cin.tie(0);
   ios::sync_with_stdio(false);
   cin>>n>>m;
   for(int i=1;i<=n;i++){
          cin>>a[i];
          insert(i,i,a[i]);
   }
   while(m--){
       int l, r, c;
       cin>>l>>r>>c;
       insert(l,r,c);
   }
   for(int i=1;i<=n;i++)s[i]+=s[i-1];
   for(int i=1;i<=n;i++)
       cout<<s[i]<<" ";
    return 0;      
}

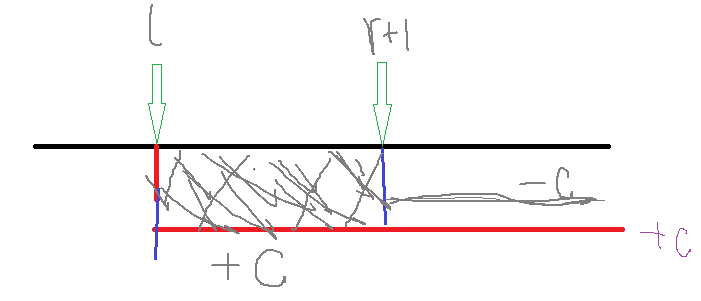
为什么操作一时b[r+1]要减去c，很简单，因为操作一我只需对[l,r]区间里的数加c，[r+1,n]这个区间里的数没必要加c，所以需要减掉c。

画图理解:

二维前缀和

给定一个n*m大小的矩阵a，有k次询问，每次询问给定x1,y1,x2,y2四个数，求以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素和。注意仍然包含左上角和右下角的元素。
画一个图吧！

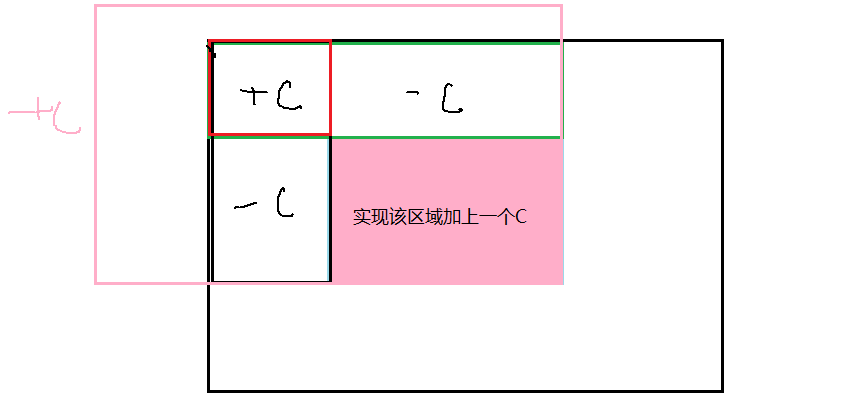
图画的很丑，希望不要介意。如图所示，按题目要求，我们每次要求的答案就是粉色圆圈所在的区域的值（注意，这里的x1,x2表示行，y1,y2表示列),对比上面这张图我们能够发现粉色区域的值等于四个区域的值减去（黑色区域+绿色区域），再减去（红色区域+红色区域)，最后因为红色区域被减了两次，我们需要再加回来。所以ans=a[x2][y2]-a[x1-1][y2]-a[x2][y1-1]+a[x1-1][y1-1]；(注意，此时的a数组代表的是前缀和)。突然想起来还没说怎么求二维前缀和，很简单，看下面代码！
题目来源

#include<iostream>

using namespace std;

const int N=1010;
int a[N][N],s[N][N];
int n,m,k;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++){
         cin>>a[i][j];
         s[i][j]=a[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1];
      }
      while(k--){
          int x1,y1,x2,y2;
          cin>>x1>>y1>>x2>>y2;
          cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;

      }
    return 0;

}

二维差分

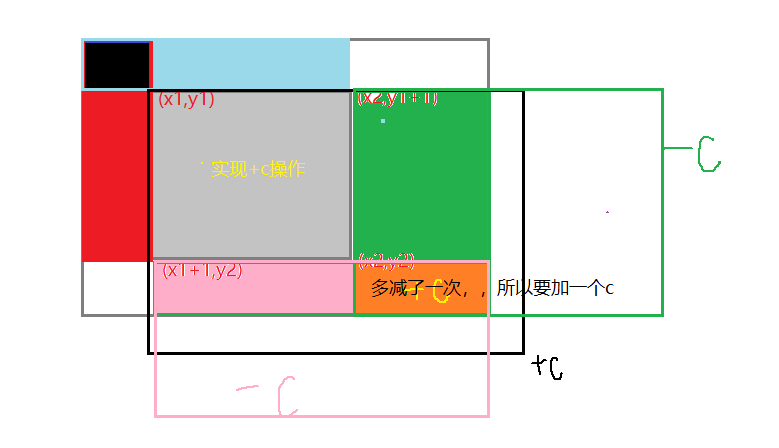
二维是和一维类似的，我们也是需要另开一个数组记录修改操作，最后求前缀和时统计修改操作，只是二维每一次操作要记录4个位置，一维只需要记录2个位置。具体怎么做，看下面画图理解吧。

题目来源

#include<iostream>
using namespace std;
const int N=1040;
int a[N][N],b[N][N];

int n,m,k;

void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y1+1]+=c;

}
int main(){
        cin.tie(0);
        ios::sync_with_stdio(false);
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
      {
          cin>>a[i][j];
          insert(i,j,i,j,a[i][j]);
      }

    while(k--){
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }

    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
         b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];

    for(int i=1;i<=n;i++)
    {
      for(int j=1;j<=m;j++)
      {
        cout<<b[i][j]<<" ";
      }
      cout<<endl;
    }

    return 0;    
}

前缀和、二维前缀和与差分的模板小总结已经完了，希望你有所收获。

模板来源与yxc老师的总结 链接

一维前缀和

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维前缀和

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：

S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

一维差分

给区间[l, r]中的每个数加上c：

B[l] += c, B[r + 1] -= c

二维差分

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：

S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c