图最短路算法的总结
前言
为什么要写这个博客?
多次在课上学过,并且在基础课和提高课里反反复复遇到很多次,可是每次碰到的时候都会觉得没有办法仅仅凭自己立刻写出来,我想主要原因是因为中间有许多小坑没有记住,并且对于细节没有理解,导致每次的思考难度总是过大。
因此趁着本次的复习,写下这篇总结博客
图
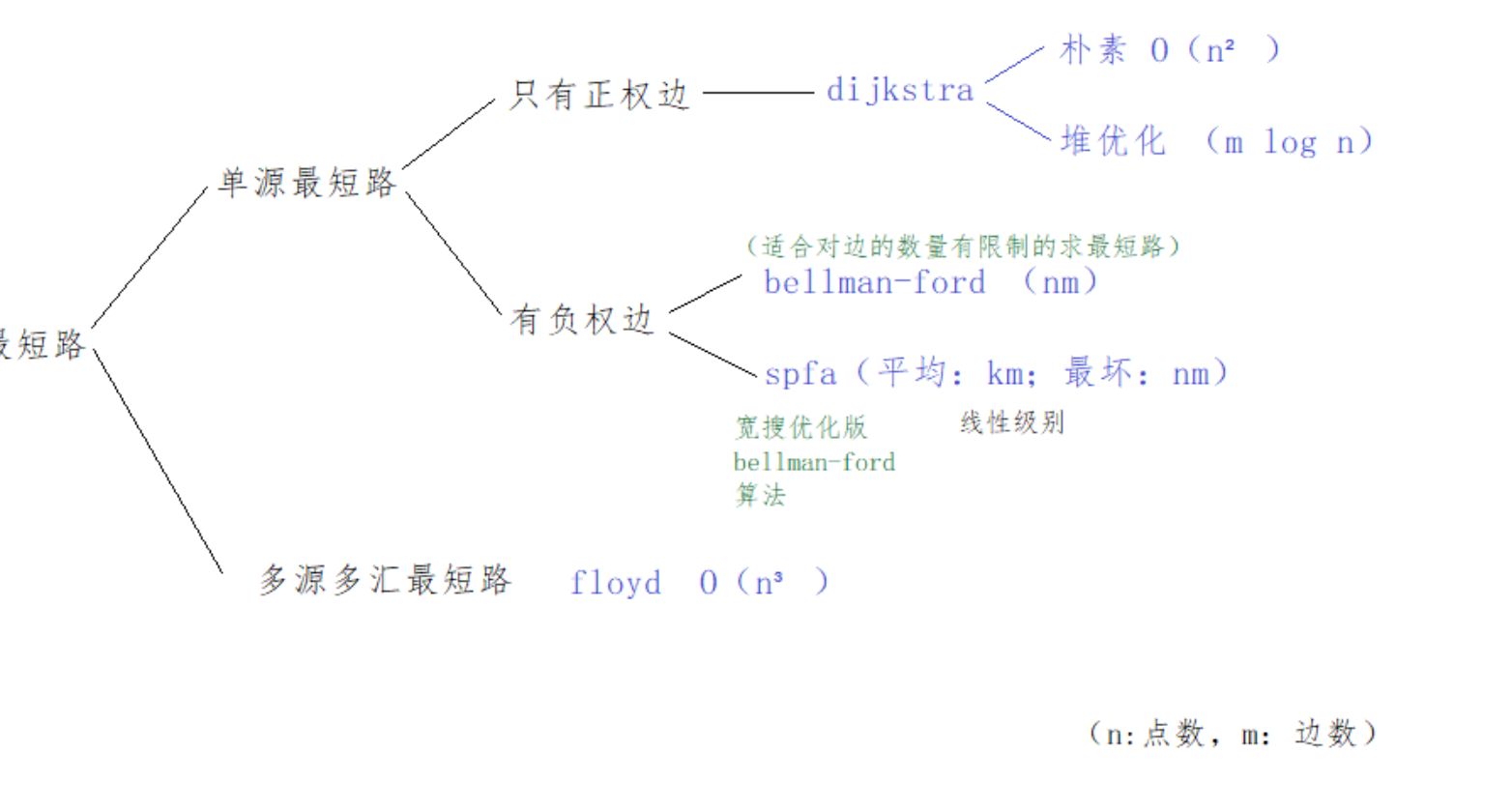
个人核心理解(从一般到特殊)
1、首先,对于有负权的一般图如何保证全图d都是最短路呢?
仅仅需要保证对于所有的边都满足三角不等式即可。(上一句话仔细想)
那么本来就只需要遍历全图的边,遍历次数足够多即可完成所有的更新。
2、当然,这里有一个问题,任何一个图最终都会满足三角不等式吗?
答案是否定的,如果存在一个负权回路,则在次数足够大之后,我们仍然无论以什么方式遍历所有边,都会导致还会有相应的点被松弛。
3、我们先假设不存在负权回路的问题,那么剩下最重要的是我们怎么确定遍历的次数呢?(bellman-ford算法的引出)
我们保守估计,一共就只有n个点,
第一次遍历,至少能找到一个只通过一条边的最短路。否则,我们可以假设所有最短路的长度都至少为2,显然不可能
那么对于第二次遍历,至少能找到一条长度为2的
依次类推,我们就得出了bellman-ford的思想
一共有n个点,因此我们只需要遍历n-1次即可。
若考虑不超过k次的,我们只需要遍历k次即可,这也就是 acwing853的题目来源,
若不严格限制边数,其实不需要加拷贝操作。
4、上一个方法时间复杂度为O(nm),我们能不能优化一下? (spfa思想引入)
显然,没必要每次全部都遍历所有的边,这是因为,我们每次松弛的时候,注意到,若对于边xy,只有当d[x]的值减小了
d[y]的值才可能被减小,而我们最开始松弛的边全都是与上一轮松弛的点邻接的点。我们用一个队列来存储d减小了的点,然后去更新他们的临点。
5、负环问题
对于一个负环,其可以被松弛无限次。
对于某点x到各个点的路径上是否有负权回路的判断,
若用bellman-ford算法,则若第n次松弛的时候,还能被更新,则显然有负环
对于spfa,用一个cnt数组,记录到这个点的边数,若边数超过了n显然有负环。
注意到,只加入一个点的话,某些负权回路可能到达不了。
解决方案:在原图的基础上新建一个虚拟源点,从该点向其他所有点连一条权值为0的有向边。那么原图有负环等价于新图有负环。此时在新图上做spfa,将虚拟源点加入队列中。然后进行spfa的第一次迭代,这时会将所有点的距离更新并将所有点插入队列中。执行到这一步,就等价于视频中的做法了。那么视频中的做法可以找到负环,等价于这次spfa可以找到负环,等价于新图有负环,等价于原图有负环
6、特殊情况,若没有负权边,则显然,一个点被更新过了之后就不会被再次更新了,每次只需要找到松弛的一个边,然后
遍历其临边即可。松弛n-1次即可
7、对于上述操作,每次找最小边实际上是最耗费时间的我们就可以用堆来优化,这就是堆优化的dij的思想
系统总结注意点,
dijkstra 朴素版
初始化
dijkstra 堆优化版
系统默认小跟堆
bellman-ford
1、防止串联
2、防止inf+负数的情况
spfa
1、这里不需要判断串联,因为不会发生在一组中串联的情况 因为更新的都是相邻点

