第十一届省赛

• A.门牌制作（5分）

题目描述:

小蓝要为一条街的住户制作门牌号。这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、0、1、7，即需要 1 个字符 0，2 个字符 1，1 个字符 7。
请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

话不多说，直接上代码:

#include<iostream>
using namespace std;
int sum=0;
void check(int n)
{
    while(n)
    {
        if(n%10==2) sum++;
        n=n/10;
    }
}
int main()
{

    for(int i=1;i<=2020;++i)
        check(i);
    cout<<sum;
    return 0;
 } 

答案:624.

• B.既约分数（5分）

问题描述:

如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。
例如，3/4,5/2,1/8,7/1都是既约分数。
请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？

答案提交:

这是一道结果填空题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

话不多说，直接上代码:

#include<iostream>
#include<bits/stdc++.h> 
using namespace std;
int sum=0;
int n;
bool check(int i,int j)
{
    if(i==j&&i!=1) return false;//通过后期验算发现正确答案比运算写出来的要+1.回头一看果然落了一种情况——1/1.所以要特判一下.
    if(i==1||j==1) return true;
    if(i<j) swap(i,j);//保证i>j;

    for(int x=j;x>1;x--)
        if(i%x==0&&j%x==0)
            return false;

    return true; 
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;++i)//分子 
        for(int j=1;j<=n;++j)//分母
            if(check(i,j)) 
                sum++;

    cout<<sum;
    return 0; 
 } 

怎样才能避免上面这种：觉着能减少一些情况，但其实思路不严谨的情况呢？————做完找些情况验证一下，多验证几个.
下面介绍更简单的思路——直接用gcb函数

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int sum=0;
    for(int i=1;i<=2020;++i)
        for(int j=1;j<=2020;++j)
            if(__gcd(i,j)==1) sum++;

    cout<<sum;
    return 0;
}

手写gcd()函数:

#include<iostream>
#include<algorithm>
using namespace std;
int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
int main()
{
    int sum=0;
    for(int i=1;i<=2020;++i)
        for(int j=1;j<=2020;++j)
            if(gcd(i,j)==1) sum++;

    cout<<sum;
    return 0;
}

关于最大公约数的具体知识

• C.蛇形填数（10分）

题目描述:

如下图所示，小明用从 1 开始的正整数“蛇形”填充无限大的矩阵。

1 2 6 7 15 …
3 5 8 14 …
4 9 13 …
10 12 …
11 …
…

容易看出矩阵第二行第二列中的数是 5。请你计算矩阵中第 20 行第 20 列的数是多少？

答案提交:

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

考试的时候一看有点懵，这怎么搞。咦，才20行20列，手动写吧…在word上了四五行发现这样写下去到交卷也写不完啊…
于是又盯着题目在看，嗯？有规律:

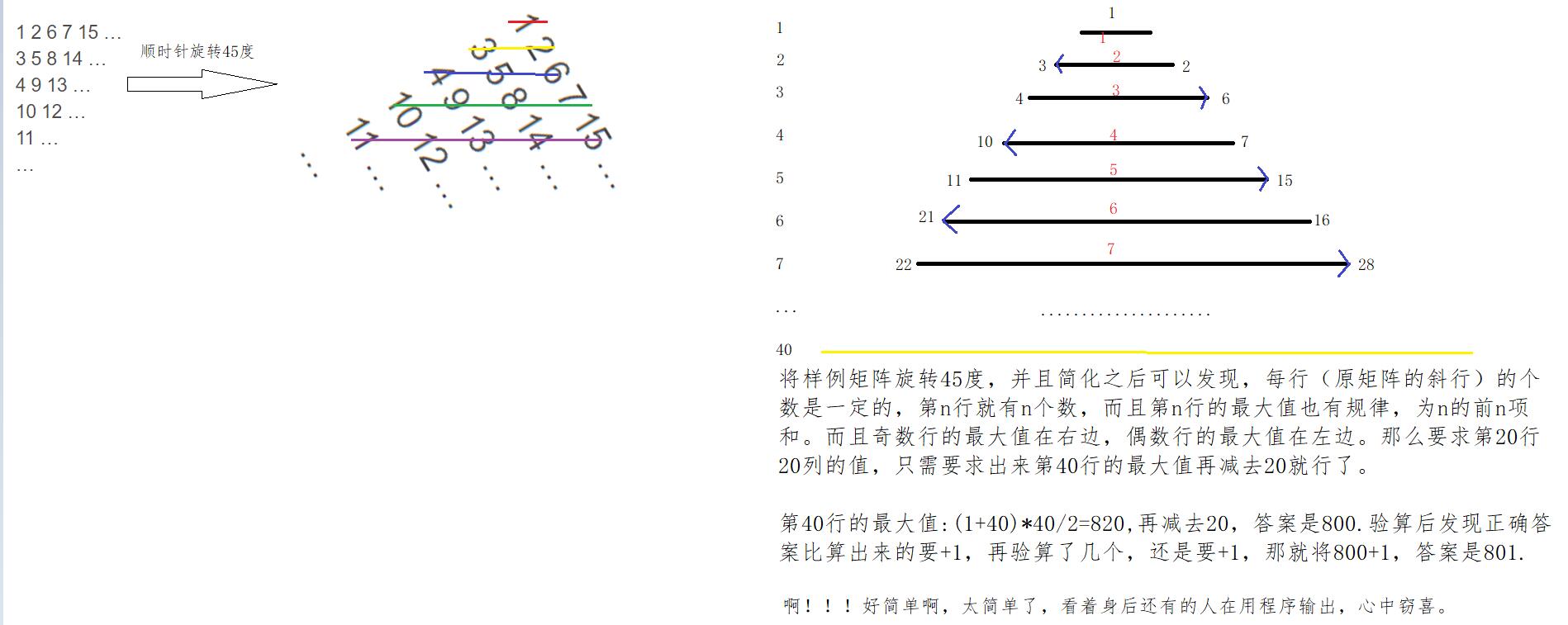
但是，出来后一对答案，其他人都是761…心里顿时sb，臭sb，让你得瑟.但是也没想为啥错了，直到出成绩进国赛了.想着用程序输出来看看吧:

//说一下思路:输入n，n的意思是第几斜行。然后求出第n斜行最大的数值是多少，然后输出这前n斜行。因为数组定义的是全局变量，所以只输出大于0的就是蛇形矩阵.
#include<iostream>
using namespace std;
int a[100][100];
int dx[]={-1,1},dy[]={1,-1};
int main()
{
    int n;
    cin>>n;
    int sum=(1+n)*n/2;

    int x=0,y=0,cnt=0;
    for(int i=1;i<=sum;++i)
    {
        a[x][y]=i;
        x=x+dx[cnt%2];y=y+dy[cnt%2];

        if(x<0){//判断是否要拐弯
            x++;cnt++;
        } 
        if(y<0){//判断是否要拐弯
            y++;cnt++;
        } 
    }
    for(int i=0;i<20;++i){
        for(int j=0;j<20;++j)
            cout<<a[i][j]<<" ";

        cout<<endl;
    }
    return 0;       
} 

运行结果如下:

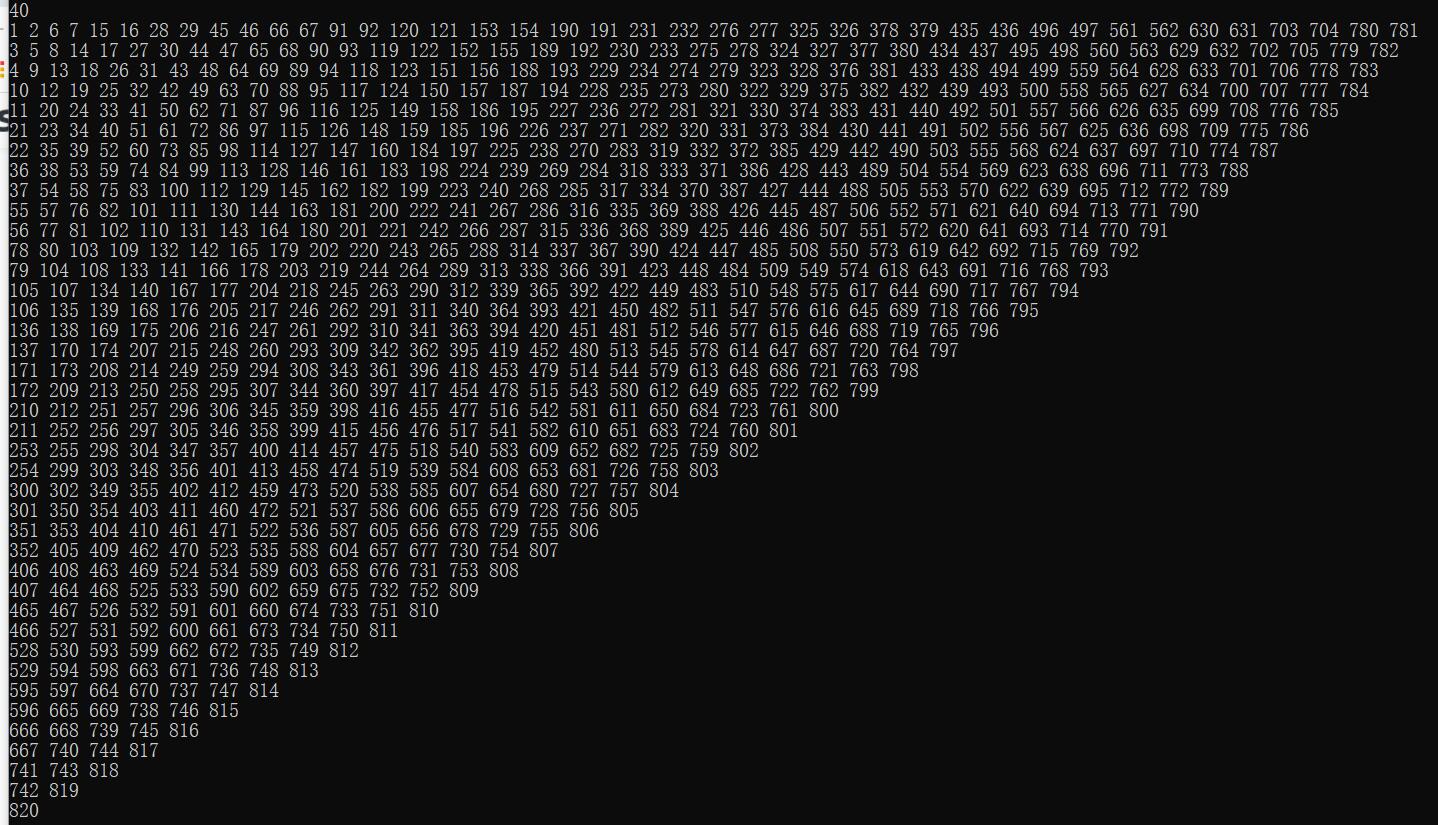
照着图片开始数，没错啊，就是801啊，为啥错了呢？数串了？又数了几遍，还是啊…
迷惑的时候又从前往后数了一遍，这次是761…
那这次程序只输出前20行20列:

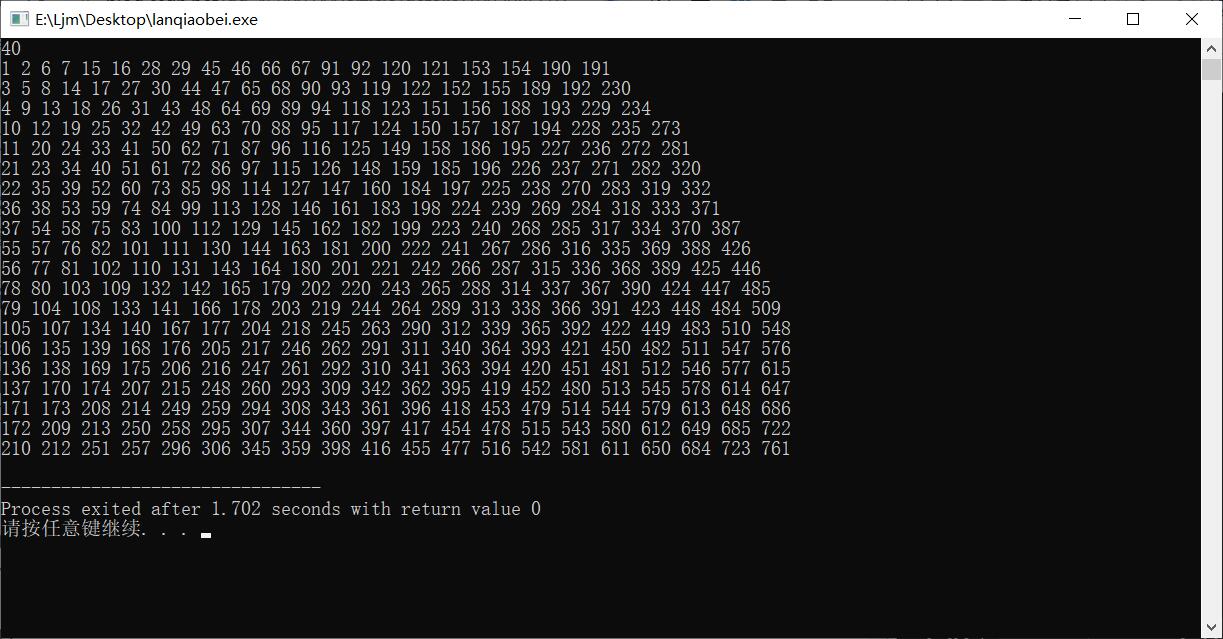
从后往前数就是错的，从前往后数就是对的，啊这，这是怎么回事呢？

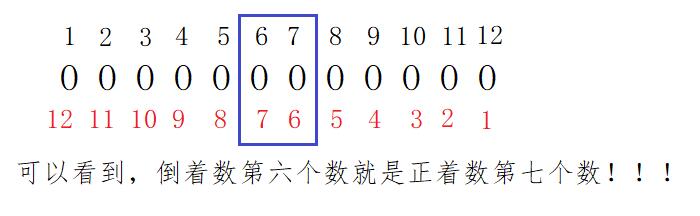
看来，当时求的第20行2列其实是第21行21列，怪不得差40呢…
这次知道厉害了,害.

• D.
• E.试题 E: 七段码（15分）

问题描述

小蓝要用七段码数码管来表示一种特殊的文字。
上图给出了七段码数码管的一个图示,数码管中一共有7段可以发光的二极管,分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

当时看完就觉着复杂也没多想就跳过去了，还剩20分钟的时候回过头来这道题还没有做。因为考试前一天做了指数型排列那道题，所以当时就冒出来一个想法，将a-g用1-7来表示，然后先输出所有的可能性。

#include<iostream>
using namespace std;
bool st[10];
int n,cnt=0;
void dfs(int step)
{
    if(step>n){
        cnt++;//计算一共输出多少种情况
        for(int i=1;i<=n;++i)
            if(!st[i]) cout<<i<<" ";

        cout<<endl;
    }
    else
    {
        st[step]=false;
        dfs(step+1);

        st[step]=true;
        dfs(step+1);
    }
}
int main()
{

    cin>>n;
    dfs(1);
    cout<<cnt; 
    return 0;       
} 

当时cnt输出的是128，一看数也不大，一咬牙，妈的手动暴力.然后将答案复制到word，一个一个验证是不是符合情况，数了三遍，80。好在没数错，答案是对的。呼~~~
F.
J.
H.
I.
* J.

第十一届国赛

第十届省赛

第十届国赛

E

#include<iostream>
using namespace std;
int a[105];
int main()
{
    int n;
    cin>>n;
    int cnt=0,i;
    for(i=1;i<=100000;++i)
    {

        cnt=0;
        for(int j=1;j<=i;++j)
            if(i%j==0)
            {
                a[cnt++]=j;
            }
        if(cnt==n)
            break;
    }
    cout<<i<<endl;
    for(int i=0;i<cnt;++i)
        cout<<a[i]<<" ";
    return 0;
}

答案:45360

第九届省赛

第九届国赛

A.换零钞

题目描述:

x星球的钞票的面额只有：100元，5元，2元，1元，共4种。
小明去x星旅游，他手里只有2张100元的x星币，太不方便，恰好路过x星银行就去换零钱。
小明有点强迫症，他坚持要求200元换出的零钞中2元的张数刚好是1元的张数的10倍，剩下的当然都是5元面额的。
银行的工作人员有点为难，你能帮助算出：在满足小明要求的前提下，最少要换给他多少张钞票吗？
(5元，2元，1元面额的必须都有，不能是0)

注意:

需要提交的是一个整数，不要填写任何多余的内容。

思路:

因为要使得钞票的数量最少，所以就让5元和2元的钞票尽量的多，1元的钞票尽量的少。
所以5元的钞票的数量就从最大值开始递减枚举，2元的钞票数量就从最小值开始递增枚举。
因为2元的张数刚好是1元的张数的10倍，所以2元的钞票数量就不用枚举。

#include<iostream>
using namespace std;
int main()
{
    bool st=false;
    for(int i=20;i>=1;i--)//5元的数量 
    {
        for(int j=1;j<200;j++)//1元的数量 
        {
            int k=j*10;//2元的数量 
            if(i*5+j*1+k*2==200)
            {
                //cout<<i<<" "<<k<<" "<<j<<endl;输出5元，2元，1元的钞票数量
                cout<<i+j+k;//最少钞票数量
                st=true;
                break;
            }
        }
        if(st) break; 
    }
    return 0;
}

B.激光样式

题目描述:

x星球的盛大节日为增加气氛，用30台机光器一字排开，向太空中打出光柱。安装调试的时候才发现，不知什么原因，相邻的两台激光器不能同时打开！国王很想知道，在目前这种bug存在的情况下，一共能打出多少种激光效果？显然，如果只有3台机器，一共可以成5种样式，即：
全都关上(sorry, 此时无声胜有声，这也算一种);开一台，共3种;开两台，只1种
30台就不好算了，国王只好请你帮忙了。要求提交一个整数，表示30台激光器能形成的样式种数。

注意:

只提交一个整数，不要填写任何多余的内容。

思路:

看完这道题立马就想起来 递归实现指数型枚举 这道题。先将30台机光器以1-30标号，然后对-30进行指数型枚举，求出来30台机器所有的开关情况，然后对每种情况进行筛选，看看有没有相邻两台机器同时开启的情况，有的话舍掉。

#include<iostream>
using namespace std;
int sum=0;//存储符合条件的情况
int n;//表示有多少台机器，好调试.
bool st[35];//存储每个灯开还是不开 
void dfs(int step)//step表示机器的标号
{
    if(step>n)
    {
        bool b=true;//默认没有相邻同时打开的 
        for(int i=1;i<n;++i)//遍历看看有无相邻同时打开的 
            if(st[i]&&st[i+1])
                b=false;//表明有相邻打开的 

        if(b) sum++;//没有相邻的机器同时打开，计数. 
    }
    else
    {
        st[step]=true;//开
        dfs(step+1);

        st[step]=false;//不开 
        dfs(step+1);
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<sum;
    return 0;
}

上面代码运行了有好几分钟，提交直接TLE，但是最后运行的结果是对的——2178309.幸亏是填空题…
下面对上面代码进行优化:
如果前面有两台机器同时开启，那么就不用再继续往下面递归了，这种情况肯定不符合，直接返回就行了。不用把30台机器全枚举一遍再看符不符合情况。

#include<iostream>
using namespace std;
int sum=0;//存储符合条件的情况
int n;//表示有多少台机器，好调试.
bool st[35];//存储每个灯开还是不开 
void dfs(int step)//step表示机器的标号
{
    if(step>n)
        sum++;//没有相邻的机器同时打开,计数. 

    else
    {
        st[step]=false;//不开 
        dfs(step+1);

        st[step]=true;//开
        if(step>1&&st[step-1])//当这个机器不是第一台机器，而且这台机器的前一台是亮的，那么就不用再往下递归了，因为肯定不符合情况 
            return;
        dfs(step+1);
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<sum;
    return 0;
}

来看一下别人的思路:也是dfs

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 1000000007
using namespace std;
typedef long long ll;
const int maxn = 2e5+5;
const double esp = 1e-12;
const int ff = 0x3f3f3f3f;
map<int,int>::iterator it;

ll ans;
int sta[52];
void dfs(int x)
{
    if(x == 31)
    {
        ans++;
        return ;
    }
    dfs(x+1);//因为sta数组是全局变量，所以初始值都是0，直接进入下一层，表示这个灯不亮 
    if(sta[x-1] == 0)//递归完这个灯不亮的情况，再递归这个灯亮的情况。但是他这里加了个条件，只有当这个灯前边的那个灯不亮的时候才让这个灯亮。 
    {
        sta[x] = 1;
        dfs(x+1);
        sta[x] = 0;//复位
    }
    return ;
}

int main()
{
    dfs(1);

    cout<<ans<<endl;

    return 0;
}

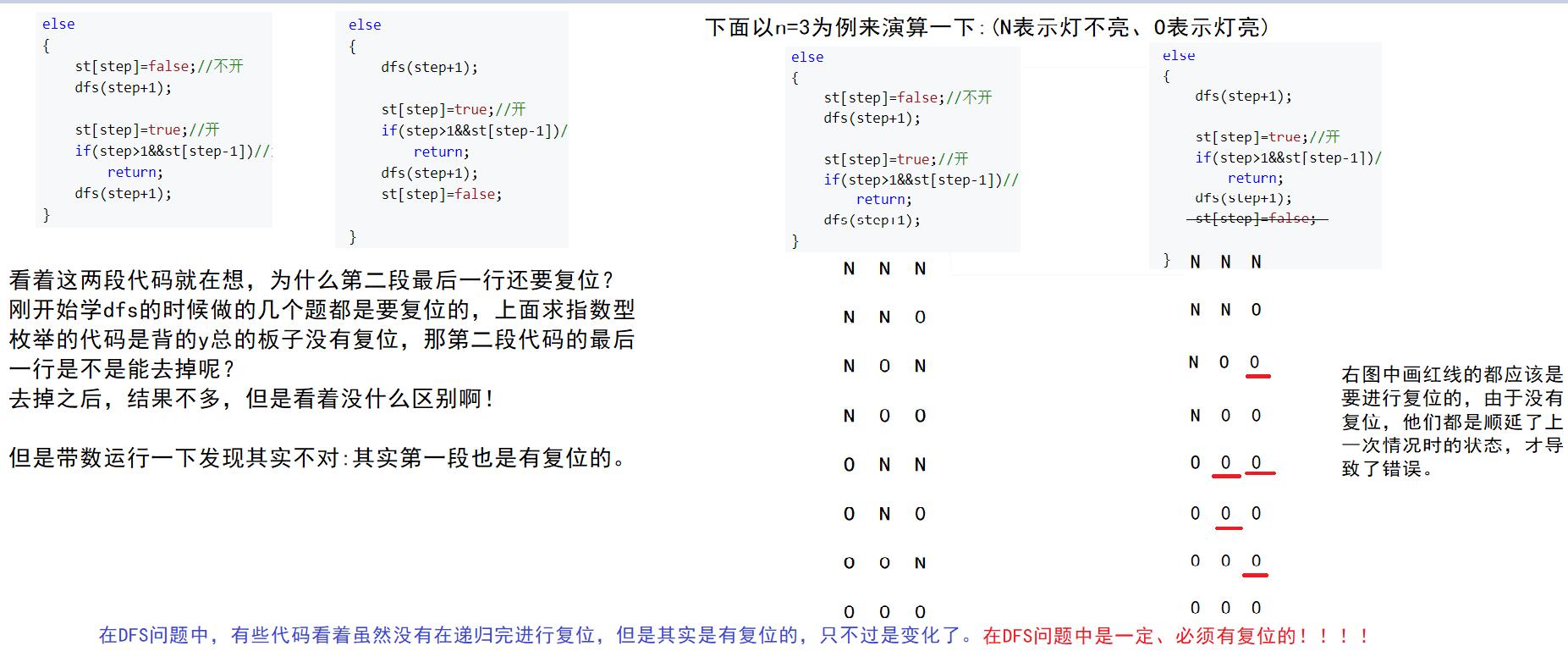
如果将我的代码变成和上边一样的话

#include<iostream>
using namespace std;
int sum=0;//存储符合条件的情况
int n;//表示有多少台机器，好调试.
bool st[35];//存储每个灯开还是不开 
void dfs(int step)//step表示机器的标号
{
    if(step>n)
        sum++;//没有相邻的机器同时打开,计数. 

    else
    {
        dfs(step+1);

        st[step]=true;//开
        if(step>1&&st[step-1])//当这个机器不是第一台机器，而且这台机器的前一台是亮的，那么就不用再往下递归了，因为肯定不符合情况 
            return;
        dfs(step+1);
        st[step]=false;

    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<sum;
    return 0;
}

C.调手表

题目描述:

格雷码是以n位的二进制来表示数。与普通的二进制表示不同的是，它要求相邻两个数字只能有1个数位不同。首尾两个数字也要求只有1位之差。
有很多算法来生成格雷码。以下是较常见的一种：
从编码全0开始生成。当产生第奇数个数时，只把当前数字最末位改变（0变1，1变0）当产生第偶数个数时，先找到最右边的一个1，把它左边的数字改变。
用这个规则产生的4位格雷码序列如下：
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
以下是实现代码，仔细分析其中逻辑，并填写划线部分缺少的代码。

#include <stdio.h>
void show(int a,int n)
{
    int i;
    int msk = 1;
    for(i=0; i<n-1; i++) msk = msk << 1;
    for(i=0; i<n; i++){
        printf((a & msk)? "1" : "0");
        msk = msk >> 1;
    }
    printf("\n");
} 

void f(int n)
{
    int i;
    int num = 1;
    for(i=0; i<n; i++) num = num<<1;

    int a = 0;
    for(i=0; i<num; i++){
        show(a,n);

        if(i%2==0){
            a = a ^ 1;
        }
        else{
            a = _________________________ ; //填空
        }
    }
}

int main()
{
    f(4);
    return 0;
}

请注意：只需要填写划线部分缺少的内容，不要抄写已有的代码或符号。

思路:

D.调手表

题目描述:

小明买了块高端大气上档次的电子手表，他正准备调时间呢。
在 M78 星云，时间的计量单位和地球上不同，M78 星云的一个小时有 n 分钟。
大家都知道，手表只有一个按钮可以把当前的数加一。在调分钟的时候，如果当前显示的数是 0 ，那么按一下按钮就会变成 1，再按一次变成 2 。如果当前的数是 n - 1，按一次后会变成 0 。
作为强迫症患者，小明一定要把手表的时间调对。如果手表上的时间比当前时间多1，则要按 n - 1 次加一按钮才能调回正确时间。
小明想，如果手表可以再添加一个按钮，表示把当前的数加 k 该多好啊……
他想知道，如果有了这个 +k 按钮，按照最优策略按键，从任意一个分钟数调到另外任意一个分钟数最多要按多少次。
注意，按 +k 按钮时，如果加k后数字超过n-1,则会对n取模。
比如，n=10, k=6 的时候，假设当前时间是0，连按2次 +k 按钮，则调为2。

输入格式

一行两个整数 n, k ，意义如题。

输出格式

一行一个整数
表示：按照最优策略按键，从一个时间调到另一个时间最多要按多少次。

样例输入

5 3

样例输出

2

样例解释

如果时间正确则按0次。否则要按的次数和操作系列之间的关系如下：
1：+1
2：+1, +1
3：+3
4：+3, +1

数据范围

对于 30% 的数据 0 < k < n <= 5
对于 60% 的数据 0 < k < n <= 100
对于 100% 的数据 0 < k < n <= 100000

资源约定：

峰值内存消耗（含虚拟机） < 256M
CPU消耗  < 1000ms

思路:

#include<iostream>
using namespace std;
int max1=0;
int main()
{
    int n,k,sum;
    cin>>n>>k;
    for(int i=1;i<=n-1;++i)
    {
        sum=i/k+i%k;
        if(sum>max1) 
            max1=sum;
    } 

    cout<<max1;
    return 0;
}

上面代码只能过一部分样例，当样例范围很大的时候，就不对了，看样对于题意的理解还不到位.

E.搭积木

F.矩阵求和
```
#include[HTML_REMOVED]

include[HTML_REMOVED]

using namespace std;
int a[10005][10005];
int main()
{
int n,sum=0;
cin>>n;
for(int i=1;i<=n;i)
for(int j=1;j<=n;j)
a[i][j]=__gcd(i,j)*__gcd(i,j);

for(int i=1;i<=n;++i)
    for(int j=1;j<=n;++j)
        sum+=a[i][j];


cout<<sum;
return 0;

}
```
上面只能过一部分算法