杂题
二分
-
二分查找(lc704)
-
lc35、lc34、lc69、lc367
- 、
双指针
//递归实现
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL||head->next== NULL)return head;
ListNode* tail= reverseList(head->next);
head->next->next = head;
head->next =NULL;
return tail;
}
};
//双指针
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL||head->next== NULL)return head;
ListNode* p = NULL;
ListNode* q = head;
while(q){
ListNode* tmp = q->next;
q->next = p;
p = q;
q = tmp;
}
return p;
}
};
```
* [19. 删除链表的倒数第 N 个结点](https://leetcode.cn/problems/remove-nth-node-from-end-of-list/)(lc19)
* [160. 相交链表](https://leetcode.cn/problems/intersection-of-two-linked-lists/)
* ==[142. 环形链表 II](https://leetcode.cn/problems/linked-list-cycle-ii/)====、====[287. 寻找重复数](https://leetcode.cn/problems/find-the-duplicate-number/)==
[环形链表思路](https://programmercarl.com/0142.环形链表II.html#思路)
```c++
//lc142
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
bool isStart = true;
while(fast && slow){
if(!isStart&&fast == slow)break;
isStart = false;
if(fast->next&&fast->next->next&&slow->next){
fast = fast->next->next;slow = slow->next;
}else return NULL;
}
while(head!=slow){
slow = slow->next;
head = head->next;
}
return head;
}
};
```
* [15. 三数之和](https://leetcode.cn/problems/3sum/)
* [18. 四数之和](https://leetcode.cn/problems/4sum/)
* ==[202. 快乐数](https://leetcode.cn/problems/happy-number/)====(快慢指针)==
## 滑动窗口
==[3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters/)==
```c++
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = s.length();
int res = 0;
unordered_set<char> set;
int r = 0;
for(int i = 0; i<len; i++){
if(i)set.erase(s[i-1]);
while(r<s.size() && set.find(s[r])==set.end()){
set.insert(s[r]);
r++;
}
res = max(res, r-i);
}
return res;
}
};
==209. 长度最小的子数组==
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0; // 滑动窗口数值之和
int i = 0; // 滑动窗口起始位置
int subLength = 0; // 滑动窗口的长度
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while (sum >= s) {
subLength = (j - i + 1); // 取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
链表
哈希表
==459. 重复的子字符串==(思想)
求能重复由 子串构成的字符串 abab. 那么两个字符串合并后中间肯定可以找出 s即 ab==abab==ab
class Solution {
public:
bool repeatedSubstringPattern(string s) {
return (s+s).substr(1, 2*s.size()-2).find(s)!=string::npos;
}
};
栈和队列
二叉树
==101. 对称二叉树== 简单题,但我感觉不太简单🥲
==110. 平衡二叉树== 简单题,我觉得不简单
class Solution {
public:
int compare(TreeNode* node){
if(node == NULL)return 0;
int rightHeight = compare(node->right);
int leftHeight = compare(node->left);
int tmpHeight = max(rightHeight, leftHeight)+1;
if(rightHeight==-1 || leftHeight==-1)return -1;
if(abs(leftHeight-rightHeight)>1)return -1;
return tmpHeight;
}
bool isBalanced(TreeNode* root) {
return compare(root)>=0;
}
};
==617. 合并二叉树==
==98. 验证二叉搜索树==(二叉搜索树的验证,很典型中序遍历查找范围的应用)
//递归法
class Solution {
public:
bool dfs(TreeNode* node, long long lower, long long up){
if(!node)return true;
if(node->val<=lower || node->val>=up)return false;
return dfs(node->left, lower,node->val)&&dfs(node->right, node->val,up);
}
bool isValidBST(TreeNode* root) {
return dfs(root, LONG_MIN, LONG_MAX);
}
};
//中序遍历
class Solution {
public:
long long tmp = LONG_MIN;
bool flag= true;
void inorder(TreeNode* node){
if(node==NULL)return;
inorder(node->left);
if(node->val<=tmp){flag = false;return;}
tmp = node->val;
inorder(node->right);
}
bool isValidBST(TreeNode* root) {
inorder(root);
return flag;
}
};
==236. 二叉树的最近公共祖先==
==701. 二叉搜索树中的插入操作==
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root == NULL)return new TreeNode(val);
if(root->val>val){
root->left = insertIntoBST(root->left, val);
}
if(root->val<val){
root->right = insertIntoBST(root->right, val);
}
return root;
}
};
==450. 删除二叉搜索树中的节点==(在二叉树中插入节点分五种情况讨论)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root)return NULL;//没有找到
if(root->val == key){
//无左右节点
if(!root->left && !root->right){
delete root;
return nullptr;
}else if(root->left && !root->right){//有左无右
TreeNode* tmp = root->left;
delete root;
return tmp;
}else if(root->right && !root->left){
auto tmp = root->right;
delete root;
return tmp;
}else{//左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
auto left = root->left;
auto right = root->right;
auto cur = right;
while(cur->left){
cur = cur->left;
}
cur->left = left;
delete root;
return right;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
==669. 修剪二叉搜索树==
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {//不在该范围中的删除即可
if(!root)return NULL;//没有找到
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
if(root->val < low ||root->val>high){
//无左右节点
if(!root->left && !root->right){
root=NULL;
return nullptr;
}else if(root->left && !root->right){//有左无右
TreeNode* tmp = root->left;
root=NULL;
return tmp;
}else if(root->right && !root->left){
auto tmp = root->right;
root=NULL;
return tmp;
}else{//左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
auto left = root->left;
auto right = root->right;
auto cur = right;
while(cur->left){
cur = cur->left;
}
cur->left = left;
root=NULL;
return right;
}
}
return root;
}
};
回溯
下面这两道题:循环中进行 dfs总搞不懂,有的地方该循环,有的地方不该,比如组合总和二中,卡到了下面的代码,其实
for(int i = start; i<candidates.size(); i++)循环内部的逻辑已经完整了,应该去掉这一层循环
//
void dfs(vector<int>& candidates, int target, int sum, int start){
if(sum>=target){
if(sum == target){
ans.push_back(tmp);
}
return;
}if(start>=candidates.size())return;
for(int i = start; i<candidates.size(); i++){
int k = i;
while(k+1<candidates.size() && candidates[i] == candidates[k+1])k++;
dfs(candidates, target, sum, k+1);
for(int j = i; j<=k; j++){
sum+=candidates[j];
tmp.push_back(candidates[j]);
dfs(candidates, target, sum, k+1);
}
for(int j = k; j>=i; j--){
tmp.pop_back();
sum-=candidates[j];
}
i = k;
//dfs(candidates, target, sum, i+1);
}
}
回溯分割类问题
==131. 分割回文串==(个人觉得很绕很典型的一道题,没做出来)93. 复原 IP 地址(两道题一起)

class Solution {
public:
vector<string> path;
vector<vector<string>> ans;
void dfs(string s, int start){
if(start>=s.size()){//走到头肯定是符合的
ans.push_back(path);return;
}
for(int i = start; i<s.size(); i++){
string tmpS = s.substr(start, i-start+1);
if(isValidRepeat(tmpS)){
path.push_back(tmpS);
dfs(s, i+1);//注意是i+1不是start+1
path.pop_back();
}else{//不符合的话走下一个
continue;
}
}
}
bool isValidRepeat(string s){
int l = 0, r = s.size()-1;
while(l<r){
if(s[l++]!=s[r--])return false;
}
return true;
}
vector<vector<string>> partition(string s) {
dfs(s, 0);
return ans;
}
};
exclusion
==491. 非递减子序列==(思想有几点很绕)即 dfs里每一层相同的元素只能出现一次,因为前面的第一次出现的该数值的元素已经囊括了我们要找的所有情况了,也就是和全排列 II原理类似 eg:1 1 2第一层选定了 1 了,1 在第一层出现后在第一层中不会再出现 1

class Solution {
public:
vector<int> path;
vector<vector<int>> ans;
void dfs(vector<int> nums, int start){
if (path.size() > 1) {
ans.push_back(path);
// 注意这里不要加return,要取树上的节点
}
unordered_set<int> set;
for(int i = start; i<nums.size(); i++){
if(path.size()&&path.back()>nums[i])continue;
if(set.find(nums[i])!=set.end())continue;
set.insert(nums[i]);
path.push_back(nums[i]);
dfs(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
dfs(nums,0);
return ans;
}
};
贪心
==135. 分发糖果==
那么本题我采用了两次贪心的策略:
- 一次是从左到右遍历,只比较右边孩子评分比左边大的情况。
- 一次是从右到左遍历,只比较左边孩子评分比右边大的情况。
==406. 根据身高重建队列==
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性

// 版本一
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
vector<vector<int>> que;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
que.insert(que.begin() + position, people[i]);
}
return que;
}
};
452. ==用最少数量的箭引爆气球== 、435. 无重叠区间
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int findMinArrowShots(vector<vector<int>>& points) {
if (points.size() == 0) return 0;
sort(points.begin(), points.end(), cmp);
int count = 1; // 记录非交叉区间的个数
int end = points[0][1]; // 记录区间分割点
for (int i = 1; i < points.size(); i++) {
if (end < points[i][0]) {
end = points[i][1];
count++;
}
}
return count;
}
};
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 1; // 记录非交叉区间的个数
int end = intervals[0][1]; // 记录区间分割点
for (int i = 1; i < intervals.size(); i++) {
if (end <= intervals[i][0]) {
end = intervals[i][1];
count++;
}
}
return intervals.size() - count;
}
};
class Solution {
public:
int monotoneIncreasingDigits(int n) {//逻辑为 231 ->229. 298->289.
string nums = to_string(n);
int flag = nums.size();
for(int i = nums.size()-2; i>=0; i--){
if(nums[i]>nums[i+1]){
flag = i;
nums[i]--;
nums[i+1] = '9';
}
}
for(int i = flag+1; i<nums.size(); i++){
nums[i] = '9';
}
return stoi(nums);
}
};
单调栈
深度搜索广度搜索
==417. 太平洋大西洋水流问题==(被恶心到)
==827. 最大人工岛==
==127. 单词接龙==
并查集应用
==684. 冗余连接==
DP
==343. 整数拆分==
class Solution {
public:
int integerBreak(int n) {
//f[i] = j*f[i-j];
int f[n+1];
memset(f, 0, sizeof f);
f[2] = 1;
for(int i = 3; i<=n; i++){
//f[i] = max(i, f[i]);
for(int j = 1; j<i; j++){//拆分是两个还是多个
f[i] = max(f[i], max(j * (i-j), j * f[i-j]));
}
}
return f[n];
}
};
==96. 不同的二叉搜索树==
原题链接
有序列的数字构成的二叉搜索树 = 相同节点数目构成的二叉树的数目。
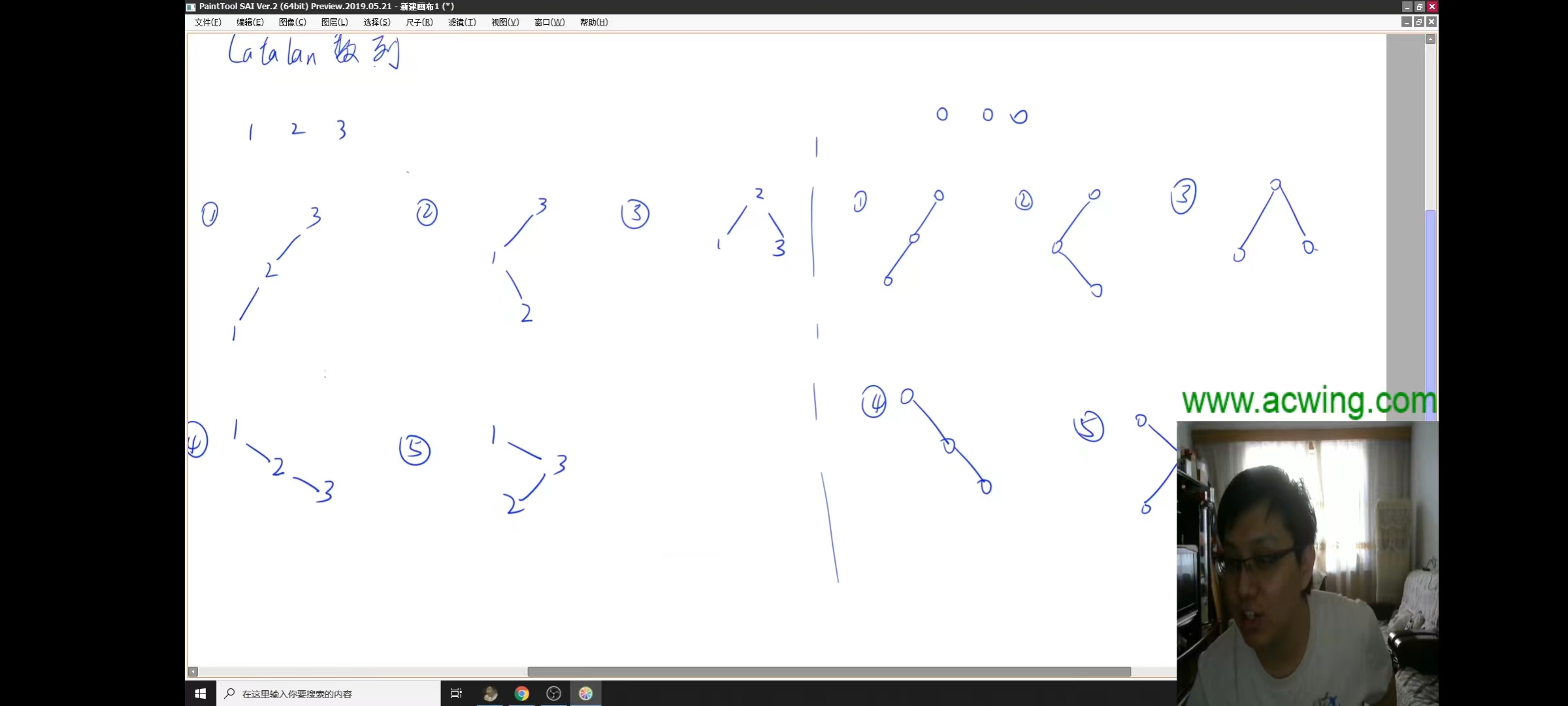
可以抽象为一棵树共有i个节点,其左右子树分别有k, i-k-1节点。f(i)为共有的二叉树状态
则$f(i)=\sum_{k=0}^{i-1} f(k) \cdot f(i-1-k)$
这个公式为卡特兰数的变形:$C_n = \frac{1}{n+1} C^{n}_{2n} $,详见题目
#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
const int MOD = 1e9+7;
int n;
typedef long long LL;
int main(){
cin>>n;
f[0] = 1;
for(int i = 1; i<=n; i++){
for(int j = 0; j<i; j++){
f[i] = (f[i] + (LL)f[j] * f[i - 1 - j]) % MOD;
}
}
cout<<f[n];
return 0;
}
0-1背包
int main(){
int n, maxV;
cin>>n>>maxV;
memset(f, 0, sizeof f);
for(int i = 1; i<=n; i++){
cin>>v[i]>>w[i];
}
for(int i = 1; i<=n; i++){
for(int j = 0; j<=maxV; j++){
f[i][j] = f[i-1][j];
if(j-v[i]>=0){
f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
}
}
}
cout<<f[n][maxV]<<endl;
}
完全 0-1 背包
int main(){
int n, m;
cin>>n>>m;
for(int i = 1; i<=n; i++)cin>>v[i]>>w[i];
memset(f, 0, sizeof f);
for(int i = 1; i<=n; i++){
for(int j = 0; j<=m; j++){
f[i][j] = f[i-1][j];
if(j-v[i]>=0)
f[i][j] = max(f[i][j], f[i][j-v[i]]+w[i]);
}
}
cout<<f[n][m]<<endl;
}

4==16. 分割等和子集==(转化为 0-1 背包)
class Solution {//f[j]以 j为最大容量能装下的最多数值
public:
int f[20010];
long long sum;
bool canPartition(vector<int>& nums) {
for(int i = 0; i<nums.size(); i++){
sum+=nums[i];
}
if(sum%2)return false;
for(int i = 0; i<nums.size(); i++){
for(int j = sum/2; j>=nums[i]; j--){
f[j] = max(f[j], f[j-nums[i]]+nums[i]);
}
}
if(f[sum/2] == sum/2)return true;
return false;
}
};
1==049. 最后一块石头的重量 II==
class Solution {
public:
int f[30][3010];
int sum;
int lastStoneWeightII(vector<int>& stones) {
for(int i = 0; i<stones.size(); i++){
sum+=stones[i];
}
int target = sum/2;
for(int i = stones[0]; i<=sum/2; i++){
f[0][i] =stones[0];
}
for(int i = 1; i<stones.size(); i++){
for(int j = 0; j<=sum/2; j++){
if(j-stones[i]>=0){
f[i][j] = max(f[i-1][j], f[i-1][j-stones[i]]+stones[i]);
}else{
f[i][j] = f[i-1][j];
}
}
}
cout<<f[stones.size()-1][target]<<endl;
return sum-f[stones.size()-1][target]-f[stones.size()-1][target];
}
};
==494. 目标和==(第一遍用的 dfs过了,没找出如何迁移到背包问题中)
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
/**left-right = target;
left+right = sum;
left = (sum+target)/2
*/
int sum = 0;
for(int i = 0; i<nums.size(); i++){
sum+=nums[i];
}
int f[20010];
cout<<(sum+target)/2<<endl;
if(sum<abs(target) ||(sum+target) %2 == 1)return 0;
int res = 0;
memset(f, 0, sizeof f);
f[0] = 1; //f[i]表示最大填充重量为i的方案数
for(int i = 0; i<nums.size(); i++){
for(int j =(sum+target)/2; j>=nums[i] ; j--){
f[j]+=f[j-nums[i]];
}
}
return f[(sum+target)/2];
}
};
class Solution {
public:
int f[101][101];
int findMaxForm(vector<string>& strs, int m, int n) {
int size = strs.size();
int l[size+1];
int r[size+1];
memset(l, 0, sizeof l);
memset(r, 0, sizeof r);
for(int i = 0; i<size; i++){
for(int j = 0; j<strs[i].size(); j++){
if(strs[i][j] == '0')l[i]++;
else r[i]++;
}
}
for(int i = 0; i<size; i++){
for(int j = m;j>=l[i]; j--){
for(int k = n; k>=r[i]; k--){
f[j][k] = max(f[j][k], f[j-l[i]][k-r[i]]+1);
}
}
}
return f[m][n];
}
};
0-1 背包问题总结
- 纯 0 - 1 背包 (opens new window) 是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集 (opens new window) 是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II (opens new window) 是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和 (opens new window)474. 一和零 是求 给定背包容量,装满背包有多少种方法。
完全背包
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
//518
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
int f[amount+1];
int f2[amount+1];
memset(f, 0, sizeof f);
f[0]=1;
for(int i = 0; i<n; i++){
for(int j = coins[i]; j<=amount; j++){
f[j] += f[j-coins[i]];
}
}
return f[amount];
}
};
//377
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
long long f[1010];
memset(f, 0, sizeof f);
f[0] =1;
for(int j = 0; j<=target; j++){
for(int i = 0; i<nums.size(); i++){
if(j>=nums[i] && f[j] < INT_MAX - f[j - nums[i]]) f[j]+=f[j-nums[i]];
}
}
return f[target];
}
};
==322. 零钱兑换==
这三道题类型一模一样
//322
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
int f[amount+1];
memset(f, 0, sizeof f);
int f2[amount+1];//f[j]表示该金额下最少硬币数量
memset(f2, 0x3f, sizeof f2);
f2[0] = 0;
for(int i = 0; i<n; i++){
for(int j = coins[i]; j<=amount; j++){
f[j] = max(f[j], f[j-coins[i]]+coins[i]);//当前容量最大金额数量
if(f[j] == j){
f2[j] = min(f2[j], f2[j-coins[i]]+1);
}
}
}
return f2[amount] == 0x3f3f3f3f ? -1: f2[amount];
}
};
淘天笔试题,染色最少次数,给定一串数字,初始都是白色,有两种染色策略:1.一次可以染一个数字 2.一次可以染一个去剪[l,r]但是需要保证 a[l]!=a[r]问最少染色次数
#include <bits/stdc++.h>
using namespace std;
#define all(a) begin(a), end(a)
#define int long long
int n, m;
//染色问题
void solve() {
cin >> n;
vector<int> a(n);
for (auto &i : a) cin >> i;
int l = 0;
while (a[0] == a[l] and l < n) l++;
if (l == n)
cout << n << "\n";
else {
if (a[0] != a[n - 1]) {
cout << "1\n";
} else {
set<int> S;
for (int i = 0; i < n; i++) {
if (a[i] != a[0]) {
S.emplace(i);
}
}
int ans = INT_MAX;
auto it = S.begin();
while (next(it) != S.end()) {
ans = min(ans, 1LL + *next(it) - *it);
cout<<ans<<" ";
it = next(it);
}
cout<<endl;
vector<int> dp1(n);
vector<int> dp2(n);
for (int i = n - 1; i >= 0; i--) {
if (i + 1 < n and a[i] == a[i + 1]) {
dp1[i] = dp1[i + 1] + 1;
} else {
dp1[i] = 1;
}
}
for (int i = 0; i < n; i++) {
if (i > 0 and a[i] == a[i - 1]) {
dp2[i] = dp2[i - 1] + 1;
} else {
dp2[i] = 1;
}
}
ans = min(dp1[0] + 1LL, ans);
ans = min(dp2[n - 1] + 1LL, ans);
cout << ans << "\n";
}
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int __;
cin >> __;
while (__--) solve();
return 0;
}
1 1 2 2 3 2 1 1 1 1 1

