离散化与区间合并笔记

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

离散化与区间合并笔记

作者：

wuog , 2019-08-05 00:05:42 , 所有人可见 , 阅读 2606

17

18

离散化

首先我们先理解一下什么是离散化!
离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。(人话该这样说：就是原数据在区间太过于分散，我们要将它放到一个小的空间里面进行处理)！！
或者说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

例如我要你处理10^18这样的类似数据本身很大，而且还十分分散，但是数据只有几十个，这些数据自身无法作为数组的下标保存对应的value值。如果这时只是需要你处理这些数据，你当然不能用一个超级大的数组，那样空间与时间利用会超出范围，那么可以对其进行离散化处理。当数据只与它们之间的相对大小有关，而与具体是多少无关时，可以进行离散化。

所以离散化的重点就是将那些散乱的数字映射到有序的数组里面下面看具体操作：

例如：
设有4个数：
1234567、123456789、12345678、123456
排序：123456<1234567<12345678<123456789
=>1<2<3<4
那么这4个数可以表示成：2、4、3、1
例如：
    原数据：1,999,100000,15；处理后：1,3,4,2；
    原数据：{100,200}，{20,50000}，{1,400}；处理后：{3,4}，{2,6}，{1,5}；

到这里你可能就似乎明白离散化就是处理一些改进一个低效的算法问题，甚至实现根本不可能实现的算法。

STL 算法离散化

思路是：
   1.先排序
   2.再删除重复元素
   3.最后就是索引元素离散化后对应的值。

   是不是感觉就像你让一群分散的人根据一些条件排队，然后来领东西；


 假定待离散化的序列为a[n]，b[n]是序列a[n]的一个副本，则对应以上三步为：

sort(sub_a,sub_a+n);

int size=unique(sub_a,sub_a+n)-sub_a;
//size为离散化后元素个数

  for(i=0;i<n;i++)
  a[i]=lower_bound(sub_a,sub_a+size,a[i])-sub_a + 1;
//k为b[i]经离散化后对应的值

对于第3步，若离散化后序列为0,1,2,...,size-1则用lower_bound，从1,2,3,...,size则用upper_bound。
其中lower_bound返回第1个不小于b[i]的值的指针
而upper_bound返回第1个大于b[i]的值的指针

bound函数
当然在这个题中也可以用lower_bound然后再加1得到与upper_bound相同结果，两者都是针对以排好序列。使用STL离散化大大减少了代码量且结构相当清晰。当然我们也可以用二分的方法去解决。

例题

1.模板（1）

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

2.模板（2）

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
     int a=alls.size()-1;
     return  lower_bound(alls,alls + a,x)-alls;
     //该函数详解请参照cppAPI
}

3.unique函数
(类似双指针的处理)

vector<int>::iterator unique(vector<int> &a)
{
    int j = 0;
    for (int i = 0; i < a.size(); i ++ )
        if (!i || a[i] != a[i - 1])
            a[j ++ ] = a[i];
    // a[0] ~ a[j - 1] 所有a中不重复的数

    return a.begin() + j;
}

unique函数

例题

例题来源
代码：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

typedef pair<int ,int>PII;

const int N=300010;
int n,m;
int a[N],s[N];
vector<int> alls;
vector<PII> add,query;

int find(int x){
    int l=0,r=alls.size()-1;
    while(l<r){
        int mid=(l+r)>>1;
        if(alls[mid]>=x)r=mid;
        else l=mid+1;
    }
    return r+1;
}
int main(){
    cin>>n>>m;

    for(int i=0;i<n;i++){
        int x,c;
        cin>>x>>c;
        add.push_back({x,c});

        alls.push_back(x);

    }

    for(int i=0;i<m;i++){
        int l,r;
        cin>>l>>r;
        query.push_back({l,r});

        alls.push_back(l);
        alls.push_back(r);


    }
    //排序
    sort(alls.begin(),alls.end());

    //去重
    alls.erase(unique(alls.begin(),alls.end()),alls.end());

    //加上某一个值
    for(auto item:add){
        int x=find(item.first);
      a[x]+=item.second;
    }

    //前缀和
    for(int i=1;i<=alls.size();i++)
      s[i]=s[i-1]+a[i];


    for(auto item:query)
    {
        int l=find(item.first),r=find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;

}

区间合并

我们先来理解一下啊什么是区间合并！
假如给定 n 个闭区间[ai,bi]，其中i=1,2,…,n。任意两个相邻或相交的闭区间可以合并为一个闭区间。例如，[1,2]和[2,3]可以合并为[1,3]，[1,3]和[2,4]可以合并为[1,4]，但是[1,2] 和 [3,4] 不可以合并。
我们的任务输出区间合并后的数量;

其实这个问题本质就是看各个小区间的端点值，我们换一个图来理解一下：
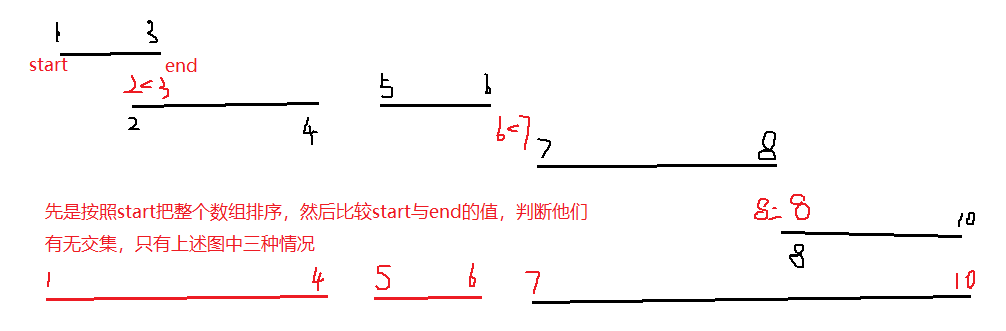
捕获.PNG

模板

// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res;
    //排序
    sort(segs.begin(), segs.end());
    //给端点赋值
    int st = -2e9, ed = -2e9;

    //循环合并
    for (auto seg : segs)//核心技术

        if (ed < seg.first)// 第一种情况 7>6
        {
            // 一个简单的赋值过程
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }

        else ed = max(ed, seg.second);// 第二种与第三种情况 2<3 8=8

    if (st != -2e9) 
         res.push_back({st, ed});  //写入区间段

    segs = res;
}

   该题最重要的就是模拟端点比较三种情况

例题

例题链接

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring> 
using namespace std;

typedef pair<int,int> PII;
vector<PII> segs;

int n;
void merge(vector <PII> &segs){
    vector<PII> res;
    sort(segs.begin(),segs.end());
    int st=-2e9,ed=-2e9;
    for(auto s:segs){
        if(ed<s.first){
            if(st!=-2e9)res.push_back({st,ed});
            st=s.first,ed=s.second;
        }
        else ed=max(ed,s.second);
    }
    if(st!=-2e9)res.push_back({st,ed});
    segs=res;
}

int main(){
    cin>>n ;
    for(int i=0;i<n;i++){
        int l,r;
        cin>>l>>r;
        segs.push_back({l,r});
    }
    merge(segs);
    cout<<segs.size()<<endl;
    return 0;
}

小结

1.离散化的难点是映射，如何排序？然后如何将他们有序化？
2.区间合并就一个动态模拟合并的三种情况。
谢谢你的阅读，希望您能有所收获。

ycx 老师模板链接

离散化（例题一）

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

区间合并（例题二）

// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end());

    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);

    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}