单向链表
我们要学习单向链表就要先了解一下链表这个数据结构:
是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而顺序表相应的时间复杂度分别是O(logn)和O(1)。
使用链表结构可以克服数组需要先知道数据大小的缺点,链表结构可以充分利用内存空间。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
组成:
链表通常由一连串节点组成,每个节点包含任意的实例数据和一或两个用来指向上一个/或下一个节点的位置的链接。
链表最明显的好处就是,数据的访问往往要在不同的排列顺序中转换。而链表是一种自我指示数据类型,因为它包含指向另一个相同类型的数据的指针。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取,这也是链表的一个缺点。
链表有很多种不同的类型:单向链表,双向链表以及循环链表。
好了,看了这些我们来看一下单向链表:
因为链接方向是单向的,对链表的访问要通过从头部开始,依序往下读取,所以叫单向链表
一个单向链表的节点被分成两个部分。第一个部分保存或者显示关于节点的信息,第二个部分存储下一个节点的地址。单向链表只可向一个方向遍历。我们画一个图理解一下:
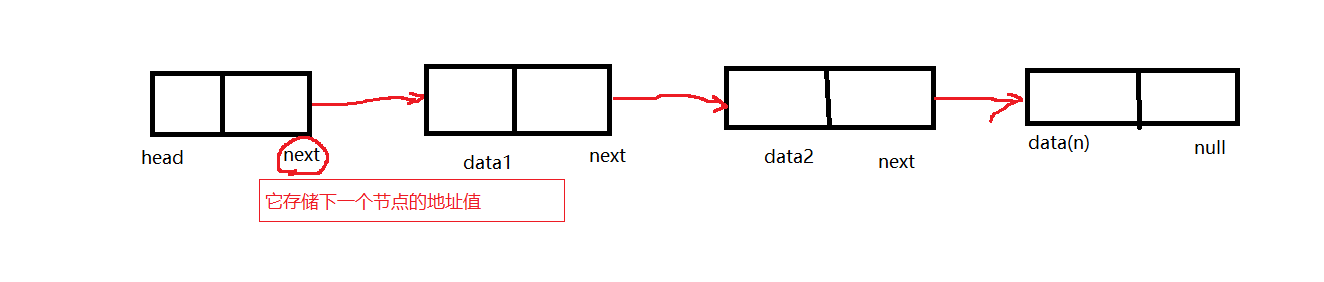
所以我们简单把他们分为数据域和指针域,数据域存储数据,指针域指向下一个存储节点的地址。
下面我们来看一下如何实现比较简单静态链表 增删改功能:
// head存储链表头,e[]存储节点的值,ne[]存储节点的next指针,idx表示当前用到了哪个节点
静态模板
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 在链表头插入一个数a
void insert(int a)
{
e[idx] = a, ne[idx] = head, head = idx ++ ;
}
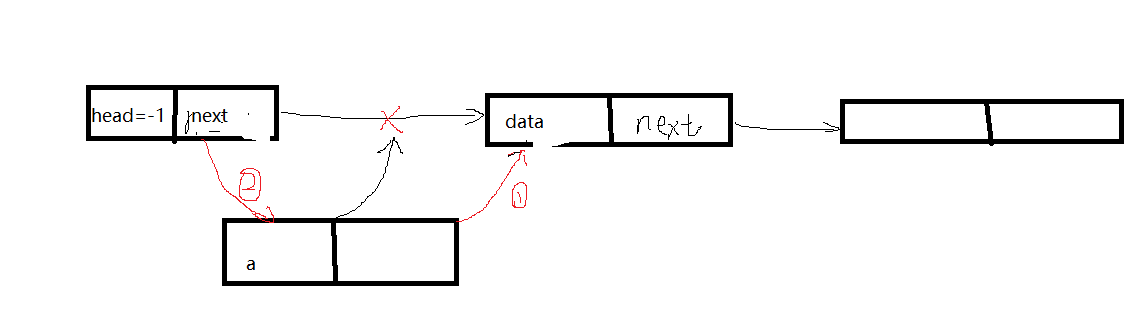
解释一下 就先把值赋到数据域,然后让head的地址值存入指针域,让idx向下移一位;
//向表中k位置插图x
void add(int k,int x){
n[idx]=x;
ne[idx]=ne[k];
ne[k]=idx++;
}
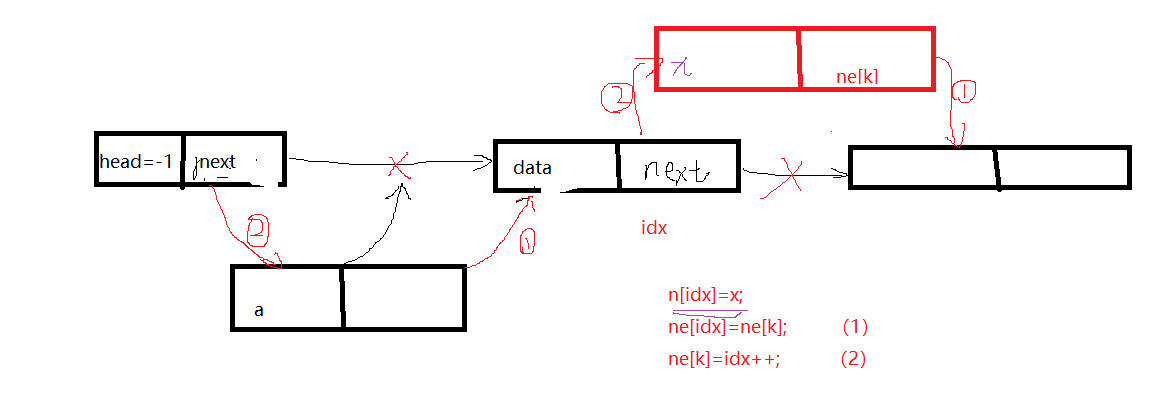
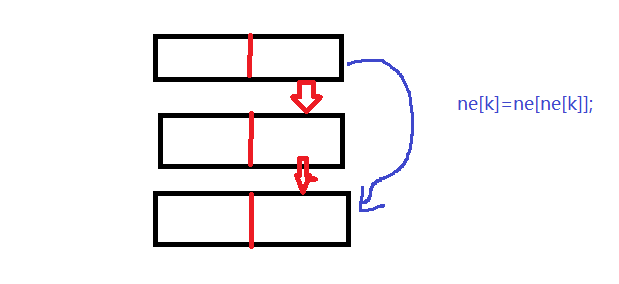
// 将k删除,需要保证头结点存在
void remove(int k)
{
ne[k]=ne[ne[k]];
}
这个与插入思想类似:
我们来看一个实际运用吧!
例题
题意:就是让我们用静态链表实现增删改功能:
代码:
#include<iostream>
using namespace std;
const int N=100010;
int idx,head,n[N],ne[N];
void add_head(int x){
n[idx]=x;
ne[idx]=head;
head=idx++;
}
void add(int k,int x){
n[idx]=x;
ne[idx]=ne[k];
ne[k]=idx++;
}
void remove(int k){
ne[k]=ne[ne[k]];
}
int main(){
head=-1;idx=0;
cin>>a;
while(a--){
string op;
int k,x;
cin>>op;
if(op=="D")
{
cin>>k;
if(!k)head=ne[head];
remove(k-1);
}
else if(op=="H")
{
cin>>x;
add_head(x);
}
else if(op=="I"){
int k,x;
cin>>k>>x;
add(k-1,x);
}
}
for(int i=head;i!=-1;i=ne[i])
cout<<n[i]<<" ";
return 0;
}
动态模板
这个是静态的,让我们看一下动态的单向链表:
typedef int ElemType;
struct LNode {
ElemType data;
struct LNode *next;
} LNode, *LinkList;
//初始化
void init(LinkList *L) {
*L = (LinkList)malloc(sizeof(struct LNode));
if (!*L) //存储分配失败
exit(-1);
(*L)->next = NULL;
}
//获取元素个数(长度)
int Length(LinkList L) {
int i = 0;
LinkList p = L->next; // p指向第一个结点
while (p) { // 没到表尾
i++;
p = p->next;
}
return i;
}
//查找
int Find(LinkList L, int i, ElemType *e) {
int j = 1; // j为检索
LinkList p = L->next; // p指向第一个结点
while (p && j < i) { // 顺指针向后查找,直到p指向第i个元素或p为空
p = p->next;
j++;
}
if (!p || j > i) // 第i个元素不存在
return 0;
*e = p->data; // 取第i个元素
return e;
}
bool Insert(LinkList L, int i, ElemType e) {
// 表L中第i个位置之前插入元素e
int j = 0;
LinkList p = L, s;
while (p && j < i - 1) { // 寻找第i-1个结点
p = p->next;
j++;
}
if (!p || j > i - 1) // i小于1或者大于表长
return false;
s = (LinkList)malloc(sizeof(struct LNode)); // 动态地分配内存空间,生成新结点
s->data = e; // 插入L中
s->next = p->next;
p->next = s;
return true;
}
bool Delete(LinkList L, int i, ElemType *e) {
int j = 0;
LinkList p = L, q;
while (p->next && j < i - 1) { // 寻找第i个结点,并令p指向其前驱结点
p = p->next;
j++;
}
if (!p->next || j > i - 1) // 删除位置不合理
return flase;
q = p->next; // 删除并释放结点
p->next = q->next;
*e = q->data;
free(q);
return true;
}
当然他还有其他的功能我们这里就不一一列举,有兴趣的童鞋就去看cpp底层代码或者API文档。
双向链表
有了单向链表的基础,我们就可以很好的去理解双向链表,下面我们来看一下:
它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。他弥补了单向链表的缺点,一般我们都构造双向循环链表。
画个图看看:

动态模板
struct DuLNode {
ElemType data;
struct DuLNode *prior, *next;
} DuLNode, *DuLinkList;
//初始化
void init(DuLinkList *L) {
*L = (DuLinkList)malloc(sizeof(DuLNode));
(*L)->next = (*L)->prior = *L;
}
//判断是否为空
bool is_Empty(DuLinkList L) {
if (L->next == L && L->prior == L)
return true;
else
return false;
}
//获取长度
intLength(DuLinkList L) {
int i = 0;
DuLinkList p = L->next; // p指向第一个结点
while (p != L) { // p没到表头
i++;
p = p->next;
}
return i;
}
//查找
int Find(DuLinkList L, int i, ElemType *e) {
int j = 1; // j为索引值
DuLinkList p = L->next; // p指向第一个结点
while (p != L && j < i) { // 顺指针向后查找,直到p指向第i个元素或p指向头结点
p = p->next;
j++;
}
if (p == L || j > i) // 第i个元素不存在
return 0;
*e = p->data; // 取第i个元素
return e;
}
// L中第i个位置之前插入元素e,i的合法值为1<=i<=l.length+1,否则无法在第(length+1)个结点之前插入元素
boll Insert(DuLinkList L, int i, ElemType e) {
DuLinkList p, s;
if (i < 1 || i > ListLength(L) + 1) // i值不合法
return ERROR;
p = GetElemP(L, i - 1); // 在L中确定第i个元素前驱的位置指针p
if (!p) // p=NULL,即第i个元素的前驱不存在(设头结点为第1个元素的前驱)
return false;
s = (DuLinkList)malloc(sizeof(DuLNode));
if (!s)
return OVERFLOW;
s->data = e;
s->prior = p; // 在第i-1个元素之后插入
s->next = p->next;
p->next->prior = s;
p->next = s;
return true;
}
// 表L的第i个元素,i的合法值为1<=i<=length
bool Delete(DuLinkList L, int i, ElemType *e) {
DuLinkList p;
if (i < 1) // i值不合法
return true;
p = GetElemP(L, i); // 在L中确定第i个元素的位置指针p
if (!p) // p = NULL,即第i个元素不存在
return ERROR;
*e = p->data;
p->prior->next = p->next; // 此处并没有考虑链表头,链表尾
p->next->prior = p->prior;
free(p);//释放空间
return false;
}
静态模板
由于静态模板是由动态实例化出来的,所以我们在这里不做过多的解释。
其原理和过程就是动态数组
int m;
int e[N], prior[N], next[N], idx;
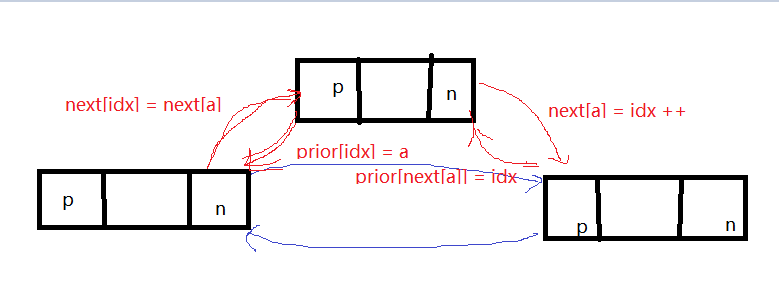
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
e[idx] = x;
prior[idx] = a, next[idx] = next[a];
prior[next[a]] = idx,next[a] = idx ++ ;
}
// 删除节点a
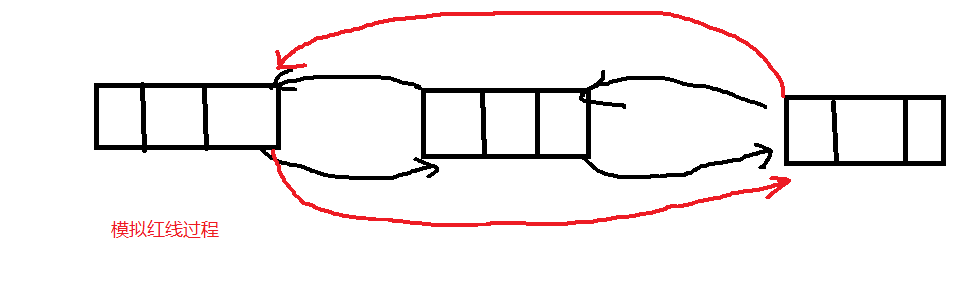
void remove(int a)
{
prior[next[a]] = prior[a];
next[prior[a]] = next[a];
}
例题
例题练习
ac代码(参考)
#include <iostream>
using namespace std;
const int N = 100010;
int m;
int e[N], l[N], r[N], idx;
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
e[idx] = x;
l[idx] = a, r[idx] = r[a];
l[r[a]] = idx, r[a] = idx ++ ;
}
// 删除节点a
void remove(int a)
{
l[r[a]] = l[a];
r[l[a]] = r[a];
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> m;
// 0是左端点,1是右端点
r[0] = 1, l[1] = 0;
idx = 2;
while (m -- )
{
string op;
cin >> op;
int k, x;
if (op == "L")
{
cin >> x;
insert(0, x);
}
else if (op == "R")
{
cin >> x;
insert(l[1], x);
}
else if (op == "D")
{
cin >> k;
remove(k + 1);
}
else if (op == "IL")
{
cin >> k >> x;
insert(l[k + 1], x);
}
else
{
cin >> k >> x;
insert(k + 1, x);
}
}
for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
cout << endl;
return 0;
}
小结
由于链表动态太过于复杂,我们一般都是用静态去解决链表问题,当然动态模板才是本质,例如leetcode上面的链表专题, leetcode链表专题 ,其实链表就和一般数组一样,只是他们的索引值形式不同,一般数组是有序的索引,而链表是地址值来连接的,所以我们可以将他视为一个数组,只是索引值处理不同罢了,由于内容过多,可能错误就非常多,希望大家能客观看待,有错误就发给我,谢谢,希望你有所收获。
yxc老师的模板 链接
单链表 —— 模板题 AcWing 826. 单链表
// head存储链表头,e[]存储节点的值,ne[]存储节点的next指针,idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 在链表头插入一个数a
void insert(int a)
{
e[idx] = a, ne[idx] = head, head = idx ++ ;
}
// 将头结点删除,需要保证头结点存在
void remove()
{
head = ne[head];
}
双链表 —— 模板题 AcWing 827. 双链表
// e[]表示节点的值,l[]表示节点的左指针,r[]表示节点的右指针,idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;
// 初始化
void init()
{
//0是左端点,1是右端点
r[0] = 1, l[1] = 0;
idx = 2;
}
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
e[idx] = x;
l[idx] = a, r[idx] = r[a];
l[r[a]] = idx, r[a] = idx ++ ;
}
// 删除节点a
void remove(int a)
{
l[r[a]] = l[a];
r[l[a]] = r[a];
}


棒!