konig定理的说明以及一些思考

首先进行以下步骤：
1、求出二分图的最大匹配。
2、从左部未匹配点出发，进行一次匈牙利算法（必定失败，否则匹配数+1，与最大匹配矛盾），对所有访问过的点进行标记。
那么，取左边未标记的点和右边标记的点，就得到最小点覆盖。

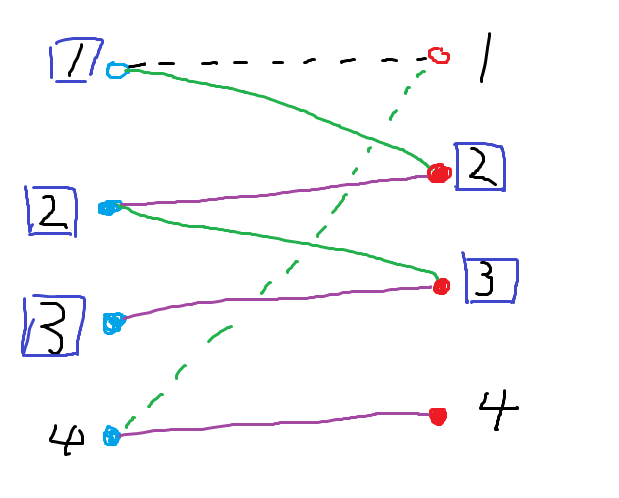
图的说明：

数字表示点编号，如果数字有方框说明在第2步该点被标记。
如果点被涂实，表面该点在最大匹配中。
紫色的线表示最大匹配中的匹配边。
绿色的线表示在二分图但不在匹配图中的边。
虚线表示假想边，其中黑色虚线不存在，绿色虚线可以存在也可以不存在。
图中表示一种konig算法的一种基本情况。

算法流程分析

图中只有左1未匹配，则dfs(1)。
依次访问的点有：左1 -> 右2 -> 左2 -> 右3 -> 左3。
由于到左3后未发现增广路径，所以dfs失败。
最终选择的最小覆盖的点为：左4、右2、右3。
左4和右4与左侧匹配未匹配点无关联，因此没被标记，但可能与右侧未标记点有边（左4与右1）。

对于左侧未标记点，左4连接了右侧匹配点右4和未匹配点右1；对于右侧标记点与之对称，连接了左侧匹配点左2和未匹配点左1，显然这些点就可以覆盖二分图且最小。

同时可以看出：
1、对于匹配边的两个点，在dfs中要么全被标记，要么全不标记
2、右侧的非匹配点不会被标记，否则找到一条增广路径。

最小覆盖点数3 = 最大匹配边数3，定理结论正确。

一些思考：

如果左侧表示男生，右侧表示女生。
1、在最大匹配后，剩下的男女要么喜欢的的已经有对象，要么没有喜欢的。
2、剩下的男女宁可单着也不愿将就（图中男1喜欢女2，但女2已有男友2，但男1不会选择女1，尽管女1现在单身。或者女1也可能喜欢男4，但就是不会和男1在一起）。
3、想要脱单要选择有备胎的，这样脱单几率才会提高。图中如果左1选择右4，则由于左4有备胎右1，这种情况左1能够上位（找到增广路径）。
4、konig是一个构造性证明，从构造过程可以看出，最终被选作最小覆盖的点，是那些既有对象还有备胎的点（左4、右2、右3）。这种点在二分图中扮演了关键角色，每条边（关系）都和他们有关联，即这种人才能够在情场左右逢源。