最长子序列的dp分析也不难,重点是如何把题目意思转化为一个最长上升子序列问题

最长上升子序列

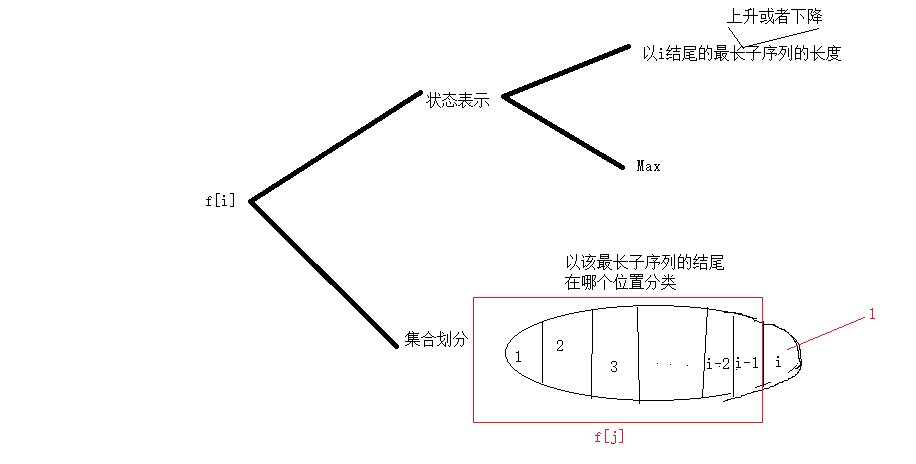
最长上升子序列模型

for(int i=1;i<=n;i++)
{
    f[i]=1;
    for(int j=1;j<i;j++)
        if(a[i]>a[j]) f[i]=max(f[j]+1,f[i]);
}

最长下降子序列模型

for(int i=1;i<=n;i++)
{
    f[i]=1;
    for(int j=1;j<i;j++)
        if(a[i]<a[j]) f[i]=max(f[j]+1,f[i]);
}

从某点向两端做LIS

数据特点呈一个开口向上或者向下的勾
开口向上
1017. 怪盗基德的滑翔翼

开口向下
1014. 登山
482. 合唱队形

//开口向上是从两端都做最长下降子序
for(int i=n;i>=n;i--)
{
    f[i]=1;
    for(int j=n;j>i;j--)
        if(a[i]<a[j]) f[i]=max(f[j]+1,f[i]);
}
//开口向下是从两端都做最长上升子序
for(int i=n;i>=n;i--)
{
    f[i]=1;
    for(int j=n;j>i;j--)
        if(a[i]>a[j]) f[i]=max(f[j]+1,f[i]);
}

如何转化成LIS问题(特点)

数据之间存在严格的大于小于关系,新进来的数大于之前所有数,而不是仅仅大于前一个
拿 1012. 友好城市举例

• 由题意,我们可以知道,两个申请不会矛盾的条件是a1<a2,则b1<b2.
• 那么拿一条边来整体考虑,需要a值小于a’的那么b值也要小于b’, a值大于a’的那么b值也要大于b’
• a值呈现明显的大小关系,那么我们可以先对a进行排序,依次考虑每个a,因为a已经满足了严格的大于小于关系,那么就只需要考虑b的大小关系,那么对于某个ai来说,能修的边应该就需要b<bi(b为1~i-1中小于bi的数)
• 但是仅仅满足小于bi够吗？由于要保证能修的边b互相不存在矛盾,那么b之间应该也要满足相应的大小关系
• 综上考虑,相当于寻找到严格递增的b

该题就变成了以a标签排好序的数组b,进行求最长上升子序列

Diworth定理

一个序列中下降子序列的最少划分数个数等于最长上升子序列的长度。
一个序列中上升子序列的最少划分数个数等于最长下降子序列的长度。

1010. 拦截导弹

存储转移方案

在状态转移过程中,开一个g[i]数组,记录以i结尾的子序列是从第j个中哪个元素转移过来的

打印的结果是逆序的.

 for(int i=1;i<=n;i++)
        {
            f[i]=1;
            g[i]=i; //初始化
            for(int j=1;j<i;j++)
            {
                if(a[i]<a[j])       
                {
                    f[i]=max(f[j]+1,f[i]);
                    g[i]=j; //记录到的一定是当前元素能够构成的第一个长度最大的子序列
                }

            }
            if(f[i]>res.first)
            {
                res.first=max(f[i],res.first);
                res.second=i;   
            }
             int k;
            for(k=res.second;k!=g[k];k=g[k])
            {
                cout<<a[k]<<" ";
            }
            cout<<a[k]; //最后一个元素要记得打印
            cout<<endl;

        }