第十五届蓝桥杯考前抱佛腿
1、dfs深度搜索遍历问题
模板题
第十四届蓝桥杯真题
2、二分法
(1)整数二分
//区间[l,r]被划分为[l,mid]和[mid+1,r]时使用:
int bsearch_1(int l,int r)
{
while(l<r)
{
int mid=l+r>>1;
if(check(mid)) r=mid; //check()判断mid是否满足性质
else l=mid+1;
}
return 1;
//区间[l,r]被划分为[l,mid-1]和[mid,r]时使用:
int bsearch_2(int l,int r)
{
while(l<r)
{
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
return 1;
}
3、线性DP问题
模版题
AcWing 898. 数字三角形
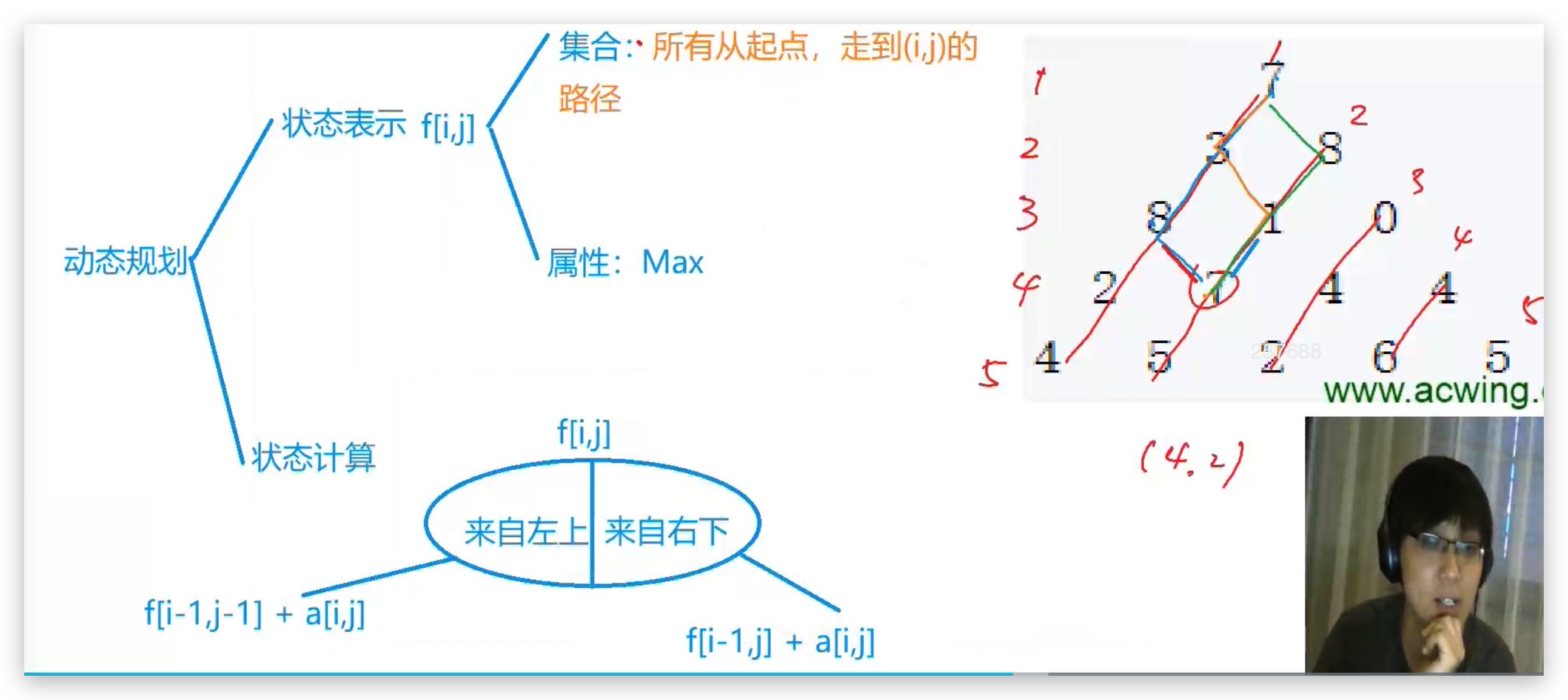
【注】
涉及到f[i-1]这种下标,i应该从1开始循环,将f[0]设置为0;
为了不处理边界问题,将状态数组先初始化为-无穷,从0开始初始话,每行都要初始化够,在状态转移中,所有用到的状态变量都需要初始化为负无穷;
#include<algorithm>
#include<iostream>
using namespace std;
const int N =510;
const int INF=1e9;
int n;
int a[N][N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
f[i][j]=-INF;
}
}
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
}
}
int res=-INF;
for(int i=1;i<=n;i++)
{
res=max(f[n][i],res);
}
printf("%d",res);
return 0;
}
AcWing 895. 最长上升子序列
【注】状态计算划分依据:f[i]表示以第i个数结尾的所有上升子序列的集合,我们要得到这个集合中的最大值,集合中每个元素长度的最大值,我们在状态计算中,划分依据是他的上一个数是原序列中的第几个数,可以分为i类,这个以第【i】个数结尾的上升子序列的上一个数,可以没有,可以是原序列中的第一个数到原序列中的第i-1个数,综上所述,椭圆中可以划分为i个小方格。
#include<iostream>
#include<algorithm>
using namespace std;
const int N =1010;
int n;
int a[N];
int f[N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(a[i]>a[j])
{
f[i]=max(f[j]+1,f[i]);
}
}
}
int res=1;
for(int i=1;i<=n;i++)
{
res=max(res,f[i]);
}
printf("%d",res);
return 0;
}
896. 最长上升子序列 II
【注1】这里对于时间复杂度进行了优化,使用了贪心的思想:对于同样长度的上升子序列来说,自然是末尾数字越小越好,这样后面进行拓展的可能性越高。
例子:
1 9 10 11 12 2 3 4 5 6 7
得到:
st: 1
st: 1 9
st: 1 9 10
st: 1 9 10 11
st: 1 9 10 11 12
st: 1 2 10 11 12
st: 1 2 3 11 12
st: 1 2 3 4 12
st: 1 2 3 4 5
st: 1 2 3 4 5 6
st: 1 2 3 4 5 6 7
st中保存的是以st[i]为结尾的最长子序列的长度,只需要保证长度最长,不需要保证序列稳定。
新进来的元素要不就在末尾增加,要不就替换掉第一个大于等于他的元素。
替换第一个大于大于他的数的目的是:为了给未来做到更长铺好路。
如果是替换操作:说明我在保持以我为结尾的最长子序列不变的同时,可以让未来能够变得更长!
如果是加在末尾:说明以我为结尾,能够让最长的长度加1了!
上述的例子,从2开始就进行不断的替换,显然,到了6这个地方,就不再是替换了,而是增加了长度!这就是前面的2~5的替换,为6和7的到来铺好了路。
#include<iostream>
#include<algorithm>
using namespace std;
const int N =100010;
int n;
int a[N];
int f[N];//维护的“最长上升子序列”,并非严格的上升子序列
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
int len=1;
f[1]=a[1];
for(int i=2;i<=n;i++)
{
int l=1,r=len;
while(l<r)
{
int mid=(l+r)>>1;
if(a[i]<=f[mid]) r=mid;
else l=mid+1;
}
if(l==len && a[i]>f[l])
{
len++;
f[l+1]=a[i];
}
else
{
f[l]=a[i];
}
//for( int j=1;j<=len;j++)
//{
// printf("%d ",f[j]);
//}
// cout<<endl;
}
printf("%d",len);
return 0;
}
897. 最长公共子序列
f[i][j]:A前i个字符,B前j个字符的公共子序列 的集合
属性:maxlen
集合划分:
情况1:a[i],b[j] 均存在于 最长公共子序列中 (前提a[i]==b[j])
情况2:a[i] 在,b[j] 不在 (无前提)
情况3:a[i],b[j] 均不在 (无前提)
情况4:a[i]不在,b[j]在 (无前提)
情况1:暂用f[i-1][j-1]+1表示
情况2:暂用f[i][j-1]表示
情况3:暂用f[i-1][j-1]表示
情况4:暂用f[i-1][j]表示
对于情况2暂用f[i][j-1]表示:
f[i][j-1]的含义是A前i个字符,B前j-1个字符的最长公共子序列长度 –>②
a[i]在不在该最长公共子序列中 并不一定,可能在也可能不在。
而情况2 的限制是:a[i] 一定在,b[j]一定不在 最长公共子序列中 –>①
很显然①是②的子集,即②包含了①,并不一定为①
那么我们可以继续 使用f[i][j-1]来表示情况2 吗?
答案是不可以的,但我们可以用它来表示 情况2和情况3
因为 对于 f[i][j-1],首先 a[j]一定不在 最长公共子序列中
其次,a[i]可能在 也可能不在,所以我们得到的 也就是f[i][j-1]其实是
a[i]在时 的最长公共子序列的长度 和 a[i]不在时的长度 的最大值
同理:f[i-1][j] 不能表示情况4,但可以用来表示 情况3和情况4
我们需要 求得的是 max(情况1,情况2,情况3,情况4)
而:f[i-1][j-1]+1 可以表示情况1 –> a
f[i][j-1]=max(情况2,情况3) –> b
f[i-1][j]=max(情况3,情况4) –> c
所以我们最终只需要 求 max(a,b,c) 即可
#include<iostream>
#include<algorithm>
using namespace std;
const int N =1010;
int n,m;
char a[N],b[N];
int f[N][N];
int main()
{
scanf("%d",&n);
scanf("%d",&m);
cin>>a+1>>b+1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j]=max(f[i][j-1],f[i-1][j]);
if(a[i]==b[j]) f[i][j]=max(f[i-1][j-1]+1,f[i][j]);
}
}
printf("%d",f[n][m]);
return 0;
}
蓝桥杯竞赛真题:
AcWing 4958. 接龙数列
分析
(1)状态计算部分:定义f[i]为以第i个数结尾的接龙数列的集合,该集合的属性为所以集合长度的最大值;
(2)状态分析部分:以第i个数结尾的接龙数列,那个前一个数是原集合中的哪个数?有i种情况,前一个数不存在,前一个数是原集合中的第1~i-1个数,由此f【i】即为其中的最大值加上a【i】
代码实现:
朴素版本dp:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =100010;
int l[N],r[N];
int f[N];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
char num[20];
scanf("%s",num);
l[i]=num[0]-'0';
r[i]=num[strlen(num)-1]-'0';
}
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(l[i]==r[j])
{
f[i]=max(f[j]+1,f[i]);
}
}
}
int res=1;
for(int i=1;i<=n;i++)
{
res=max(f[i],res);
}
printf("%d",n-res);
}
优化:开一个新的数组g[i],这个数组的作用是负责记录所有以i这个数字结尾的最长接龙数组的长度,这样的话,可以去掉一层循环,从而降低时间复杂度。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =100010;
int l[N],r[N];
int f[N];
int g[N];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
char num[20];
scanf("%s",num);
l[i]=num[0]-'0';
r[i]=num[strlen(num)-1]-'0';
}
for(int i=1;i<=n;i++)
{
f[i]=1;
// printf("i:%d g[l[i]]: %d\n",i,g[l[i]]);
f[i]=max(f[i],g[l[i]]+1);
//printf("f[i]:%d\n",f[i]);
g[r[i]]=max(f[i],g[r[i]]);
//printf("i:%d g[r[i]]: %d\n",i,g[r[i]]);
}
int res=0;
for(int i=1;i<=n;i++)
{
res=max(f[i],res);
}
printf("%d",n-res);
}
AcWing 2067. 走方格
算法标签:从dfs-dp
简单的DP问题,与三角形类似
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N =40;
int n,m;
int f[N][N];
int main()
{
scanf("%d %d",&n,&m);
f[1][1]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(i==1&&j==1) continue;
if(i%2!=0|j%2!=0)
{
f[i][j]=f[i-1][j]+f[i][j-1];
// printf("i=%d j= %d f[i][j]=%d\n",i,j,f[i][j]);
}
}
}
printf("%d",f[n][m]);
return 0;
}
数据结构问题之哈希表问题
模版题
蓝桥杯真题
AcWing 2068. 整数拼接
n是去10e5的,说明整个算法的时间复杂度需要控制在nlogn以内,这个题目可以转化为,枚举Ai,当Ai固定时,我们需要寻找Aj满足题意。
[思路]:
拼接两个整数,比如说拼接12和345,那么拼接后的数字为12345 = 1210^3+345 = Aj * 10^Ki + Ai (Ki 可以表示为 length(to_string(Ai))
to_string 为将数字转换成字符串的函数。
我们需要使得拼接后的数字是K的整数,那么拼接后的整数对K取余等于0,那么我们有下面的等式:
[(Aj*10^Ki)+Ai]%K==0
上述等式做一下恒等变形,我们得到下面的等式:
(Aj * 10^Ki) % K==-1 * (Ai%K)
这个时候,我们通过枚举Ai,去寻找满足条件的Aj,累加得到最后的答案,如何去寻找满足条件的Aj呢?
首先,确定了Ai,Ki也随之确定,Ki可以取得0~10,把范围扩大,保证不重不漏,然后去开一个哈希表,即一个二维数组,s[11][N],例如,当s[2][20]表示Aj*10^2%K=20的个数。
通过枚举Ai,计算Ai%K的值,去寻找
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =100010;
typedef long long LL;
int n,k;
LL a[N];
int s[11][N];//例如s[2][20]表达的意思是,a[j]*10^2 %k 的余数等于20的个数有多少
int main()
{
//1、读入数据
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
//2、数据读入完成,开始下一步,预处理哈希数组
for(int i=1;i<=n;i++)
{
LL t=a[i]%k;
for(int j=0;j<11;j++)
{
s[j][t]++;
t=t*10%k;
}
}
//3计算全部可以的数组个数,并滤除不符合要求的
LL res=0;//用来存储不断累加的方案数目
for(int i=1;i<=n;i++)
{
LL t=a[i]%k;
int len=to_string(a[i]).size();
res+=s[len][(k-t)%k];
//判断是否重复
LL r=t;
while(len--) r=r*10%k;
if(r==(k-t)%k) res--;
}
printf("%lld",res);
return 0;
}
C++ STL简介与使用技巧
数据结构问题之并查集
并查集的作用:高效的存储和查找字符串。
并查集支持的操作:
(1)将两个集合合并
(2)询问两个元素是否在一个集合当中
基本原理:每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点,p[x]表示x的父节点。
问题1:如何判断树根 if(p[x]==x)
问题2:如何求x的集合编号:while(p[x]!=x) x=p[x];
问题3:如何合并两个集合:px是x的集合编号,py是y的集合编号。p[x]=y;
优化:在搜寻过一个路径之后,将这个路径上所有的点直接指向根节点。
在优化之后,并查集的时间复杂度基本上可以看作是O(1)的时间复杂度
并查集的核心操作:
//寻找x的祖宗节点+路径压缩
int find()
{
if(p[x]!=x) p[x]=find(p[x])
return p[x];
}
模版题
AcWing 836. 合并集合
#include<iostream>
using namespace std;
const int N =100010;
int p[N];
int n,m;
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
p[i]=i;
}
while(m--)
{
char op[2];
int a,b;
scanf("%s%d%d",op,&a,&b);
if(op[0]=='M')
{
p[find(a)]=find(b);
}
else
{
if(find(a)==find(b))
{
puts("Yes");
}
else{
puts("No");
}
}
// printf("a=%d,p[a]= %d",a,find(a));
//printf("b=%d p[b]= %d\n",b,find(b));
}
return 0;
}
837. 连通块中点的数量
注:在累加集合数量的时候,应当注意先去进行累加,再去合并,否则,累加会出现错误。
#include<iostream>
#include<cstring>
using namespace std;
const int N =100010;
int n,m;
int p[N];
int siz[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
p[i]=i;
siz[i]=1;
}
while(m--)
{
char op[5];
int a,b;
scanf("%s",op);
if(op[0]=='C')
{
scanf("%d%d",&a,&b);
if(find(a)==find(b)) continue;
siz[find(b)]+=siz[find(a)];
p[find(a)]=find(b);
}
else if(op[1]=='1')
{
scanf("%d%d",&a,&b);
if(find(a)==find(b)) puts("Yes");
else puts("No");
}
else
{
scanf("%d",&a);
printf("%d\n",siz[find(a)]);
}
}
return 0;
}

