引言

通常的数据结构，一旦进行了CRUD操作，那么数据或状态将发生变化。因此，只能够保存当前数据集的最新状态。

如果想要记录数据结构的历史版本，那么最朴素的方式就是将每一个版本都做完全备份。这样做显然会增加时间和空间开销，而且通常在进行一次操作后，发生变化的数据只占原数据集的一小部分。因此，自然的想法就是：将未改变的部分直接继承，然后多保存增量部分。

可持久化数据结构就是完成了上述想法，提升了空间效率。可持久化数据结构实现的核心是：将不变部分的指针交给新版本，增量部分开辟新内存空间，同一内存空间被多个版本数据结构通过指针访问。这种方式有点类似于浅拷贝，在创建新副本时，不变部分只是多了些指针引用而已，指针的内存就太小了，因此可以大大减少内存开销。

可持久化Trie

以Trie的持久化为例，如下图所示：

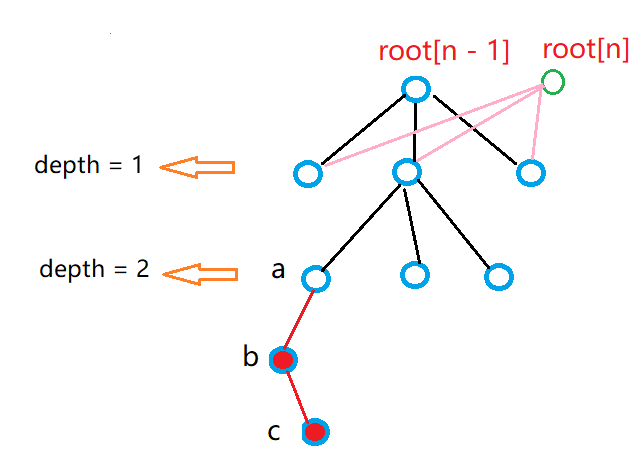
$root[n-1]$表示前一历史版本，$root[n]$表示新创建的版本。

将Trie中添加单词时，必然在某一层和上一版本不同。上图中第二层的节点a以后，是新版本独有的。

要保证新增单词是加在版本号为n的Trie中，需要跟踪该添加路径。

第一次层没有新增，因此将版本n-1的每条引用赋值给版本n。

创建第一层的中间节点t，作为以后添加新节点父节点。

递归到第二层，将原树的不变引用给节点t。

递归到第三层，这一次是新增了，与普通的Trie一样，创建新节点b，节点a指向b。

第四层的操作与第三层完全类似。

设插入的单词为str, 长度为len。从上面的过程可以看出：

• 新版版本创建了len个新节点
• 与老版本相同路径上新版本也创建了节点，这样是保证，新节点b,c只能被版本n访问到
• 不在str路径上的节点，直接将版本n-1的引用传递给版本n即可
• 虽然只有节点b,c是新增，但是该路径上也要重新创建节点

习题

以AcWing 256.最大异或和为例

题目要求
$$ a[p]\ xor \ a[p + 1] \ xor \ .... xor \ a[N] \ xor x $$
的最大值，并且满足$l \le p \le r$。

设$s[k] = a[1] \ xor \ a[2] \ xor \ … \ xor \ a[k]$，第k次向Trie插入的单词为$s[k]$，那么如果先不考虑p范围的限制，等价与找到一个k，使得：
$$ s[k] \ xor \ s[N] \ xor \ x $$
的值最大。

只要在Trie中选择与$s[N] \ xor \ x$对称的路径即可，如果没有对称路径则选择相同路径。

如果采用可持久化Trie，则$root[t]$表示插入前t个单词后的树，对于右边限制r，只需取$root[r - 1]$。

对于左限制，用$last$数组来记录每个节点能够访问到的最大单词编号。如果$last[node] \ge l - 1$，则可以选择对称路径。

代码：

#include <iostream>

using namespace std;

const int N = 600010, M = 24 * N ;

int trie[M][2], last[M], s[N], root[N], n, m, tot;

void insert(int i, int k, int p, int q) {
    if (k < 0) {
        last[q] = i;
        return;
    }
    int c = s[i] >> k &  1;
    if (p) trie[q][c ^ 1] = trie[p][c ^ 1];
    trie[q][c] = ++ tot;
    insert(i, k - 1, trie[p][c], trie[q][c]);
    last[q] = max(last[trie[q][0]], last[trie[q][1]]);
}

int query(int now, int val, int k, int limit) {
    if (k < 0) return s[last[now]] ^ val;
    int c = val >> k & 1;
    if (last[trie[now][c ^ 1]] >= limit) return query(trie[now][c ^ 1], val, k - 1, limit);
    else return query(trie[now][c], val, k - 1, limit);
}

int main() {
    cin >> n >> m;
    root[0] = ++tot;
    last[0] = -1;
    insert(0, 23, 0, root[0]);
    for (int i = 1; i <= n; i++) {
        int x;
        scanf("%d", &x);
        root[i] = ++tot;
        s[i] = s[i - 1] ^ x;
        insert(i, 23, root[i - 1], root[i]);
    }
    char op[5];
    while (m--) {
        scanf("%s", op);
        if (*op == 'A') {
            int x;
            scanf("%d", &x);
            root[++n] = ++tot;
            s[n] = s[n - 1] ^ x;     
            insert(n, 23, root[n - 1], root[n]);
        } else {
            int l, r, x;
            scanf("%d%d%d", &l, &r, &x);
            printf("%d\n", query(root[r - 1], x ^ s[n], 23, l - 1));
        }
    }
    return 0;
}