树和图的存储

一、知识点

1.树是一种特殊的图，无环连通图，所以以下只讲图。
2.图分为有向图（a->b）和无向图（a–b），但我们在算法题中如果遇到无向图，就直接（a->b）和（b->a）都建立，因此无向图就是特殊的有向图。

3.存储方法：

（1）邻接矩阵

g[a][b] = x代表a、b之间有一条长度为x的边，但这种方式不常用，因为比较浪费空间，空间复杂度为O(n²)，适合存储稠密图

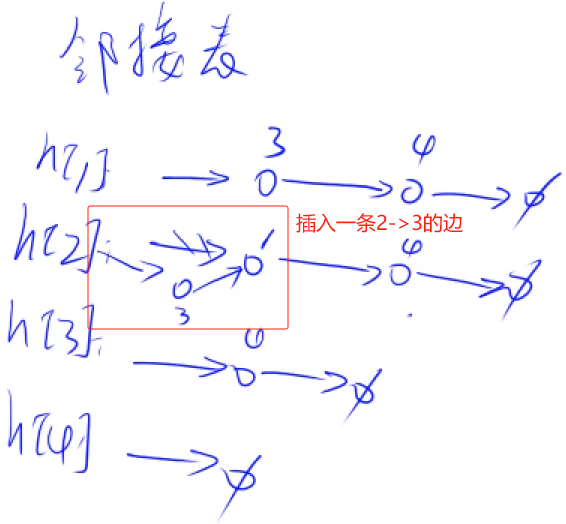
（2）邻接表

最常用的，每个点上都有一个单链表，存的是这个点可以走到哪些点。
插入边的操作：

4.时间复杂度

对于树和图的遍历，不管是DFS还是BFS，因为每个点只会被遍历一次，所以时间复杂度与点和边的数量成线性关系，为O(n + m)。

二、代码

这里的遍历只写了DFS，BFS见：树和图的BFS。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 100010, M = 2 * N;
// N代表点的个数，M代表边的条数
// n个结点的树最多有n - 1条边，如果考虑无向边需要开两倍的n - 1来存储

int n, m;
int h[N], e[M], ne[M], idx;
// h[i]：第 i 个节点的第一条邻边的 idx
// e[idx]：存储 idx 这条边的终点，也就是与第 i 个节点相连的某一个点
// ne[idx]：存储 与第 idx 条边 同起点的 下一条边的 idx，也就是邻接表中的下一个节点
// idx：用于标识每条边的下标，存的是边的编号
bool st[N];// 用于标识某点是否已经被遍历过了

// 存储：插入一条从a到b的边
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];// 新插入的边是插到链表头
    h[a] = idx++;
}

// DFS
void dfs(int u) {
    st[u] = true;// 标记一下该点被遍历到了
    // 遍历u的所有出边
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];// j是该边终点
        if (!st[j]) {// 如果该点没有被遍历过，就继续dfs
            dfs(j);
        }
    }
}

int main() {
    memset(h, -1, sizeof h);// 头节点初始化为-1
    dfs(1);
}

三、总结