查字典的Trie

作者： 作者的头像   wuog ,  2019-08-08 01:06:57 ,  所有人可见 ,  阅读 1492

9


16

Trie基础知识点

Trie，又叫字典树，字典你现在可以想一想你手上的牛津第八版词典，假设你是这本词典的主编，我们要去查找一个单词这么查，怎么添加一个热点词汇？

我们一般查找单词都是按26个字母排序去检索的，而添加也是一样的，那为什么我们可以怎么轻松去完成这些步骤？那是因为词典特有的存储方式。我们来看一下实体图：

捕获.PNG

这个就是词典和Tire的存储方式。我们还是给他一个官方的定义：

Trie树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高

其实它可以看成一个二维数组，保存一些字符串->值的对应关系。基本上，它跟Map的 HashMap 功能相同，都是 key-value 映射，是一个键值对！只不过 Trie 的 key 只能是字符串。

至于Trie树的实现，可以用数组，也可以用指针动态分配，我做题时为了方便就用了数组，静态分配空间。当然我们后面会提到动态如何去实现。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。当然后面会详细解释它。

Trie特点及方法

Trie树的基本性质可以归纳为：

（1）根节点不包含字母，除根节点意外每个节点只包含一个字母。
（2）从根节点到某一个节点，路径上经过的字符连接起来，为该节点存储的单词。
（3）每个节点的所有子节点包含的单词不相同。

Trie树有一些特性：
其实就是基本性质扩展到实际问题！
1）根节点不包含字母，除根节点外每一个节点都只包含一个字母。
2）从根节点到某一节点，路径上经过的字母连接起来，为该节点对应的单词。
3）每个节点的所有子节点包含的字母都不相同。
4）如果字母的种数为n，则每个结点的出度为n，这也是空间换时间的体现，浪费了很多的空间。
5）插入查找的复杂度为O(n)，n为单词长度。

插入，查找基本思想（以查单词为例）：

1、插入过程
对于一个单词，从根开始，沿着单词的各个字母所对应的树中的节点分支向下走，直到单词遍历完，将最后的节点标记为红色，表示该单词已插入Trie树。

2、查询过程
同样的，从根开始按照单词的字母顺序向下遍历trie树，一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色，则表示该单词不存在，若最后的节点标记为红色，表示该单词存在。

模板

好了有了一些基本点知识点，我们来用他们去解决实际问题：

  我们就想怎么去向词典中加东西，和怎么去查询一个单词是否存在？
插入

代码：

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

我们还是以画图的方式去理解：
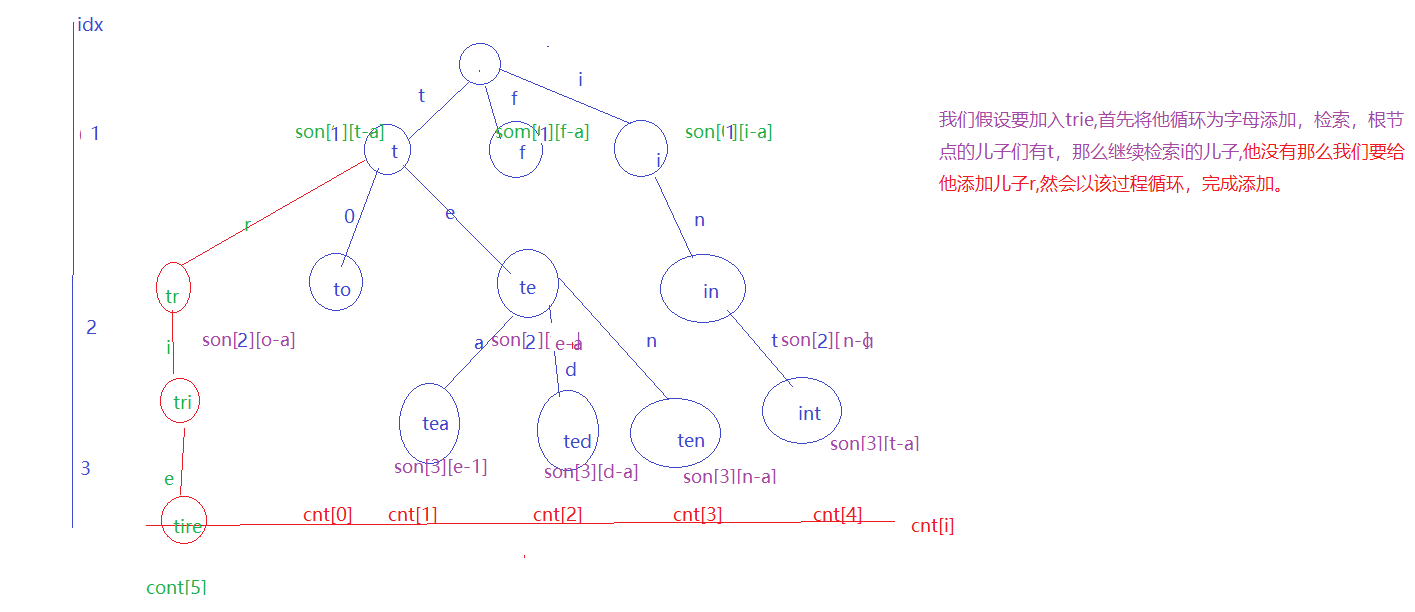
捕获00.PNG 

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}
查询

当然查询与插入思想一致，我们在这里不做过多的强调与解释！！

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}
动态实现

当然动态实现它，要注意指针的移动与及时的更新！

与静态一样在Trie树中主要有2个操作，插入、查找。一般情况下Trie树中很少存在删除单独某个结点的情况，因此只虑删除整棵树。

1、插入
假设存在字符串str，Trie树的根结点为root。i=0，p=root。
1)取str[i]，判断p->next[str[i]-‘a’]是否为空，若为空，则建立结点temp，并将p->next[str[i]-‘a’]指向temp，然后p指向temp；若不为空，则p=p->next[str[i]-‘a’]；
2)i++，继续取str[i]，循环1)中的操作，直到遇到结束符’\0’，此时将当前结点p中的 exist置为true。
2、查找
假设要查找的字符串为str，Trie树的根结点为root，i=0，p=root
1)取str[i]，判断判断p->next[str[i]-‘a’]是否为空，若为空，则返回false；若不为空，则p=p->next[str[i]-‘a’]，继续取字符。
2)重复1)中的操作直到遇到结束符’\0’，若当前结点p不为空并且st为true，则返回true，否则返回false。
3、删除
删除可以以添加的思想进行删除，它是是一个递归思想（先去查找单词，当他的父节点只有他一个儿子节点那么p->next[i] = NULL;）;

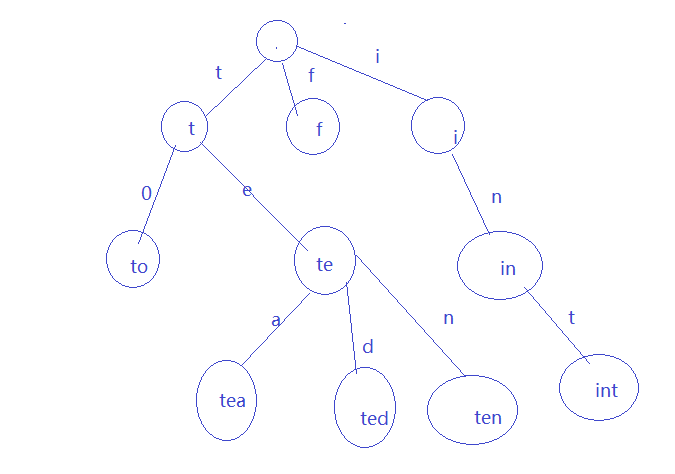
由于思想一致，所以我们再看一下这个图片：

捕获00.PNG

(与下面ac代码相比这个要复杂一点，考虑的情况更加多， 为了你理解我建议你直接去看AC的动态代码)

typedef  256 TREE_WIDTH 

typedef  128 WORDLENMAX 

struct trie_node_st {
        int idx;
        int pass;  
        struct trie_node_st *next[TREE_WIDTH];
};
struct trie_node_st root={0, 0, {NULL}};


//清空
void myfree(struct trie_node_st * rt)
{
    for(int i=0; i<TREE_WIDTH; i++){
        if(rt->next[i]!=NULL){
            myfree(rt->next[i]);
            rt->next[i] = NULL;
        }
    }
    free(rt);
    return;
}

void insert (char *word)
{
        int i;
        struct trie_node_st *curr, *newnode;

        if (word[0]=='\0')  return;
        curr = &root;
        for (i=0; ; ++i) {
                if (word[i] == '\0') {
                        break;
                }
                curr->pass++;
                if (curr->next[word[i]] == NULL)//不存在
                {
                        newnode = (struct trie_node_st*)malloc(sizeof(struct trie_node_st));//开辟空间
                        memset (newnode, 0, sizeof (struct trie_node_st));//清空
                        curr->next[word[i]] = newnode;//插入
                } 
                curr = curr->next[word[i]];//存在
        }
        curr->idx ++;
        return 0;
}

 int query (struct trie_node_st *rootp)
{
        char worddump[WORDLENMAX+1];
         int pos=0;
        int i;

        if (rootp == NULL) return 0;
        if (rootp->idx) {
                worddump[pos]='\0';
               return  rootp->idx+rootp->pass;//返回
        }
        for (i=0;i<TREE_WIDTH;++i) {
                worddump[pos++]=i;
                query(rootp->next[i]);
                pos--;
        }
        return 0;
}

习题

习题链接

题意：
就是我们词典对操作！！ 添加，查找：
AC代码：

#include<iostream>

using namespace std;

typedef long long  LL;
const LL N=1e5+5;
struct stu
{
    int son[26];                    
    int f=0;
};
stu a[N];
LL idx;
void insert(char *ch)
{
    LL i=0,p=0;             
    while(ch[i])
    {
        int x=ch[i]-'a';
        if(!a[p].son[x]) a[p].son[x]=++idx;
        p=a[p].son[x];
        i++;
    }
    a[p].f++;       
}
LL query(char *ch)
{
    LL i=0,p=0;
    while(ch[i])
    {
        int x=ch[i]-'a';
        if(a[p].son[x]==0)
            return 0;
        p=a[p].son[x];
        i++;
    }
    return a[p].f;
}
int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    LL  n;
    cin>>n;
    while(n--)
    {
        string c;
          char str[N];
        cin>>c>>str;
        if(c=="I")
            insert(str);
        else
            cout<<query(str)<<endl;
    }
}

下面就是个人比较喜欢的静态代码：

#include<iostream>

using namespace std;

const int N=200010;
int son[N][26],cnt[N],idx;
char str[N];
bool st[N];

int n;

void insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}
int query(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}
int main(){
    cin>>n;
    while(n--){
        string op;
        cin>>op>>str;
        if(op=="I")insert(str);
        else 
        cout<<query(str)<<endl;

    }
    return 0;
}

小结

Trie树其实可以他把它放到一个字典的具体实例中，你就更加能理解和操作，因为你你查词典找单词的思想是通俗易懂的，Trie 的强大之处就得益于他特有的存储方式。它的插入和查询时间复杂度都为 O(k) ，其中 k 为 key 的长度，与 Trie中保存了多少个元素无关。Hash 表号称是 O(1) 的，但在计算 hash 的时候就肯定会是 O(k)， ，而且还有存储的问题；Trie 的缺点是空间消耗很高，如果你还没有懂！！那么你可以去用词典查一下TIRE的含义是什么？然会你在回想刚才查找的过程？
其实Trie就是一个查字典的一个生活中可以用的到的算法，好了!trie知识点就是这些，谢谢你的阅读！希望你有所收获!

习题

习题一
习题二

关于题解：
可以去b站观看yxc老师@小雪菜数据结构这个一章节的讲解，或者去看相关的题解!其具体思路还是不变的，就是多了一些操作！

yxc老师的模板 链接

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

作者：yxc
链接：https://www.acwing.com/blog/content/404/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

7 评论

用户头像
Conan15   2022-02-01 18:26         踩      回复

我也来写题了，同步打卡~
写的很好，给个赞！

#include <bits/stdc++.h>
using namespace std;
int n, cnt[100010], trie[100010][30], c;
void insert(string str) {
    int q = 0;
    for (int i = 0; i < str.size(); i++) {
        int u = str[i] - 'a';
        if (trie[q][u] == 0) trie[q][u] = ++c;
        q = trie[q][u];
    }
    cnt[q]++;
}
int query(string str) {
    int q = 0, ans = 0;
    for (int i = 0; i < str.size(); i++) {
        int u = str[i] - 'a'; q = trie[q][u];
        if (q == 0) return 0;
    }
    return cnt[q];
}
int main() {
    scanf("%d", &n);
    while (n--) {
        char opt; string s;
        cin >> opt >> s;
        if (opt == 'I') insert(s);
        else printf("%d\n", query(s));
    }
    return 0;
}

上面是我的代码

用户头像
S7former   2020-10-02 10:11         踩      回复

大佬tql！

用户头像
妙WA种子_   2020-07-15 18:28         踩      回复

典型收藏比赞多Doge_

用户头像
剑指Rejection   2019-11-26 16:57         踩      回复

学到许多！

用户头像
wuog   2019-11-26 17:54         踩      回复

你这个学习速度有点快呀！hhhhh

用户头像
青柠   2019-08-30 20:52         踩      回复

果断收藏

用户头像
秦淮岸灯火阑珊   2019-08-08 15:27         踩      回复

高产啊！大佬比我强多了。