题目描述

题目链接

一棵二叉树可以按照如下规则表示成一个由 $0、1、2$ 组成的字符序列，我们称之为 “二叉树序列 $S$”：

$S= \begin{cases} 0 \ \ \ \ \ \ \ \ \ \ 表示该树没有子节点 \newline 1S_1 \ \ \ \ \ \ 表示该树有一个子节点，S_1 为其子树的二叉树序列 \newline 2S_1S_2 \ \ 表示该树有两个子节点，S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}$

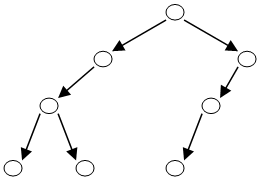
例如，下图所表示的二叉树可以用二叉树序列 $S=21200110$ 来表示。

你的任务是要对一棵二叉树的节点进行染色。

每个节点可以被染成红色、绿色或蓝色。

并且，一个节点与其子节点的颜色必须不同，如果该节点有两个子节点，那么这两个子节点的颜色也必须不相同。

给定一棵二叉树的二叉树序列，请求出这棵树中最多和最少有多少个点能够被染成绿色。

输入格式

仅有一行，表示一个二叉树序列。

输出格式

只有一行，包含两个数，依次表示最多和最少有多少个点能够被染成绿色。

数据范围

输入序列长度不超过 $5 \times 10^5$。

输入样例：

1122002010

输出样例：

5 2

解题报告

题意理解

每一个节点可以染三种颜色，红黄绿三种，要求父子节点颜色不同，而且左右儿子之间的颜色也要不同，问有多少个节点可以染色为绿色

探求算法

这是一棵树。

这棵树父子节点之前存在一定的限制关系。

题目要求最值计数

根据上面的这些分析，我们不难得出本题需要用树形DP

算法分析

既然本题要用动态规划，那么我们得严格按照，以下顺序求解本题。

1. 如何设计状态
2. 状态如何转移

首先，我们来设计状态。

状态的属性必然是，可以染绿色的节点最多是多少。

接着，根据树形DP最常见的状态设计为：

一个节点，及其子树再满足条件的情况下，答案是多少？

所以我们不难设计出：

$$ f[i]为i及其子树，满足染色条件下，可以染成绿色的节点，最多为多少。 $$

这是初级的状态设计，我们还需要通过在分析状态转移的过程中，明确如何完善状态的设计。

接下来，设计状态转移。

分析题目的限制条件，来约束状态转移，使其满足不重复不遗漏。

接下来罗列一下约束条件：

1. 父与子，节点颜色不同
2. 左右儿子，两者之间，颜色不同

那么此时我们发现，如果还是初级的状态设计，是没有办法转移的。

因为我们并不知道每个节点的染色情况，那么也无法转移了。

所以我们需要优化状态设计

$$ f[i][0/1/2]表示节点i染色为红，黄，绿，在他和他的子树都满足染色条件下，染成绿色节点最多为多少。 $$

这样，我们就彻底完成了状态设计，那么接下来开始状态转移。

如果说：

$$ a表示左儿子的染色，son_a为左儿子序号 \\\\ b表示右儿子的染色，son_b为右儿子序号 \\\\ now表示当前节点的染色，i为当前节点序号 $$

那么显然
$$ a \neq b \neq now\\\\ $$

f[x][i]=max(f[son_a][a]+f[son_b][b],f[son_a][b]+f[son_b][a]);
g[x][i]=min(g[son_a][a]+g[son_b][b],g[son_a][b]+g[son_b][a]);
//f[son_a][a]为左儿子选择颜色a，f[son_b][b]为右儿子选择颜色b
//f[son_a][b]为左儿子选择颜色b，f[son_b][a]为右儿子选择颜色a
//在这里a,b的定义不同于上面，指的是两种颜色，而且满足a,b不是当前节点的颜色
//f[x][i]为当前节点x选择颜色为i的绿色节点最大值,g[x][i]为最小值

如果说只有一个儿子节点，状态转移方程有所不同，但是和上面思路一样，具体可以直接看代码。

参考代码

//My English is poor.The Code maybe have some grammer problems.
//To have a better Font display in Acwing.com,I must choose English.
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+20;
char s[N];
int tot,tree[N][3],f[N][3],g[N][3],Size[N];
void dfs(int root)//Build the Tree
{
    Size[root]=s[root]-'0';//count the number of sons
    if (s[root]>='1')//left son
    {
        tree[root][0]=++tot;
        dfs(tot);
    }
    if (s[root]=='2')//right son
    {
        tree[root][1]=++tot;
        dfs(tot);
    }
}
void tree_DP(int x)
{
    if (Size[x]==0)//The node is a leaf node
    {
        f[x][2]=g[x][2]=1;
        return ;
    }
    for(int i=0; i<Size[x]; i++)//son
        tree_DP(tree[x][i]);
    for(int i=0; i<=2; i++)//color
    {
        int a=(i+1)%3,b=(i+2)%3;//other colors
        int son_a=tree[x][0],son_b=tree[x][1];//other sons
        if (Size[x]==1)//only a son
        {  

            f[x][i]=max(f[son_a][a],f[son_a][b]);
            g[x][i]=min(g[son_a][a],g[son_a][b]);
        }
        if (Size[x]==2)//two sons
        {
            f[x][i]=max(f[son_a][a]+f[son_b][b],f[son_a][b]+f[son_b][a]);
            g[x][i]=min(g[son_a][a]+g[son_b][b],g[son_a][b]+g[son_b][a]);
        }
        if (i==2)//the now node chooses the green color
            f[x][i]++,g[x][i]++;
        // printf("%d %d %d\n",x,f[x][i],g[x][i]);
    }
}
inline void out()//Output
{
    int ans_Min=1e9,ans_Max=0;
    for(int i=0; i<=2; i++)
    {
        ans_Min=min(ans_Min,g[1][i]);
        ans_Max=max(ans_Max,f[1][i]);
    }
    printf("%d %d\n",ans_Max,ans_Min);
}
inline void init()//Input
{
    scanf("%s",s+1);
    tot=1;
    dfs(1);
}
signed main()
{
    init();
    tree_DP(1);
    out();
    return 0;
}

更好的阅读体验

题目描述

题目链接

有一棵点数为 $N$ 的树，树边有边权。

给你一个在 $0 \sim N$ 之内的正整数 $K$，你要在这棵树中选择 $K$ 个点，将其染成黑色，并将其他的 $N-K$ 个点染成白色。

将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。

问收益最大值是多少！

输入格式

第一行两个整数 $N,K$。

接下来 $N-1$ 行每行三个正整数 $fr,to,dis$，表示该树中存在一条长度为 $dis$ 的边 $(fr,to)$。

输入保证所有点之间是联通的。

输出格式

输出一个正整数，表示收益的最大值。

数据范围

$1 \le N \le 2000$,
$0 \le K \le N$

输入样例：

5 2
1 2 3
1 5 1
2 3 1
2 4 2

输出样例：

17

样例解释

将点 $1,2$ 染黑就能获得最大收益。

解题报告

题意理解

原题很清晰，没法简析了。

探索算法

有一说一，第一眼看到这道题目，博主是真的没有认为这道题目的是一个树形DP。

但是，染色的题目，加上最值问题的要求，还是和树形DP联系很大。

那么我们为什么很难看出来呢？可能是因为我太菜了

因为我们的关注点，是一个点，它所提供的贡献。

而不是一条边，所提供的贡献

其实这也是一个难想&常见的思路。

对于树上的题目，求贡献，不是点，就是边。至少提高组范畴是这样的

那么如果说，我们按照边来思考的话，这道题目的转移方程还是很有意思的。

算法解析

类似于状态压缩动态规划，树形DP的题目，状态设计是极为重要的一步。

那么如何设计状态呢？

既然上面，我们说了，要按照边来算贡献，那么我们就先来分析边，是如何提供贡献的？

对于一条边而言，他可以提供的贡献，来自于两个节点之间的路径有它，也就是经过它：

1. 左右两边黑色节点提供的。（自己子树内的黑色节点 $ \times $ 子树外黑色节点。
2. 左右两边白色节点提供的。（自己子树内的白色节点 $ \times $ 子树外白色节点。

那么此时我们需要确定状态了

$ f[x][i] 表示节点x它到父亲节点的这条边，他的子树有i个染黑节点，此时提供的最大贡献 $

那么对于一个节点他有多少个染黑节点呢？

不知道？

那么枚举吧。

于是本题成了一个树形背包。

每个节点他的子树有多少个黑色节点（体积），然后算出这条边对答案的贡献（价值）

black_sum=s*(k-s)
white_sum=(Size[y]-s)*((n-Size[y])-(k-s)) 

$s$为当前节点他的子树有多少个染成黑色的节点

$k$为题目给出的有k个节点染成黑色

$Size[y]$表示当前节点他的子树一共有多少个节点

因此本题就这么愉快的解决了，在这里默认，树形背包DP大家都会吧。。。

如果不会的话，可以参照Acwing我曾经的背包DP的讲义。

参考代码

//My English is poor.The Code maybe have some grammer problems.
//To have a better Font display in Acwing.com,I must choose English.
#include <bits/stdc++.h>
using namespace std;
const int N=2100;
int n,k,head[N<<1],edge[N<<1],Next[N<<1],tot,Size[N];
long long f[N][N],ver[N<<1];
inline void add_edge(int a,int b,int c)
{
    edge[++tot]=b;
    ver[tot]=c;
    Next[tot]=head[a];
    head[a]=tot;
}
void tree_DP(int x,int fa)
{
    Size[x]=1;
    memset(f[x],-1,sizeof(f[x]));
    f[x][0]=f[x][1]=0;
    for(int i=head[x]; i; i=Next[i])//visit its sons
    {
        int y=edge[i];
        if (y==fa)//its father
            continue;//can't visit its father node
        tree_DP(y,x);//visit the son
        Size[x]+=Size[y];//count the Size of the tree
    }
    //Next part is the DP whose kind is knapsack.
    for(int i=head[x]; i; i=Next[i])
    {
        int y=edge[i];
        if (y==fa)//its father
            continue;//can't visit its father node
        for(int j=min(k,Size[x]); j>=0; j--)//choose black nodes whose number is j
        {
            for(int s=0; s<=min(j,Size[y]); s++)
                if (~f[x][j-s])
                {
                    long long black_sum=s*(k-s);//balck pairs
                    long long white_sum=(Size[y]-s)*((n-Size[y])-(k-s));//white pairs
                    f[x][j]=max(f[x][j],f[x][j-s]+f[y][s]+(black_sum+white_sum)*ver[i]);
                }
        }
    }
}
inline void init()
{
    scanf("%d%d",&n,&k);
    for(int i=1; i<n; i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add_edge(a,b,c);
        add_edge(b,a,c);
    }
    tree_DP(1,0);
    printf("%lld\n",f[1][k]);
}
signed main()
{
    init();
    return 0;
}