分别进行 （从上到下） 和（ 从下到上）的计算：

从下往上算 sum[u] 和 cnt[u];
因为上节点需要下面节点的信息；
先dfs（j）再更新u（先dfs子节点再更新u）

从上往下计算up[j]:
计算up[j]的时候需要计算出父节点up[u];
先更新j再dfs（j）

//从下往上的计算：u往下朝着j的方向延伸
/* u=0; (0-2-3 0-2-4 0-2-5)
j=2; (2-3 2-4 2-5)
sum[u] += sum[j]+ cnt[j] (因为需要提前获得sum[j]，所以需要从下往上计算！！)
cnt[u] += cnt[j];
/
void dfs1(int u,int father){
sum[u] = 0;
cnt[u] = 1;
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
//因为是从父节点过来的，不能重复的遍历父节点
if(j==father) continue;
dfs1(j,u);//因为需要先获得j的往下方向的信息！
//之后才能再去更新u的信息：
sum[u]+=sum[j]+cnt[j];
cnt[u]+=cnt[j];
}
}

//从上往下的计算方式：
/**
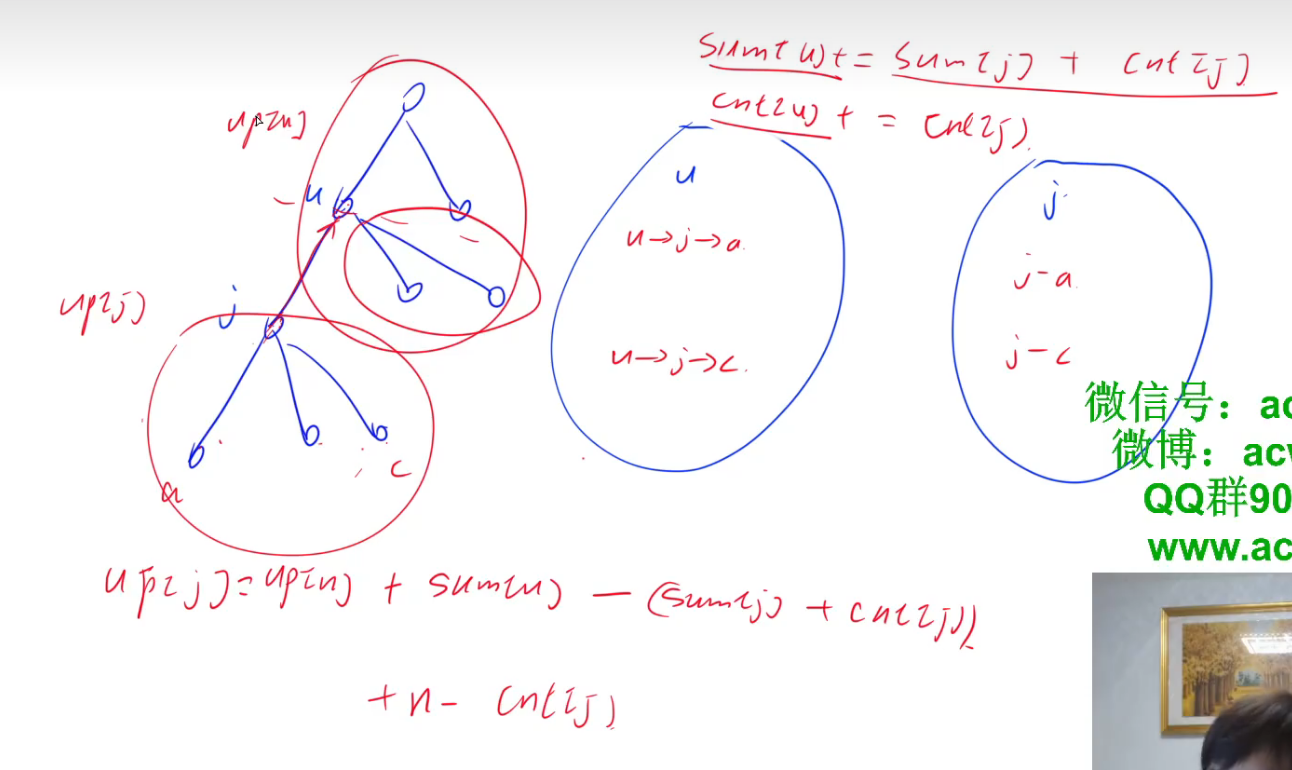
   up[j] = up[u] + sum[u] - (sum[j] + cnt[j]) + n-cnt[j]
   up[u] ：u节点的往上延伸的节点的数量；
   sum[u]: u节点往下延伸的节点的数量，往下的其中一个分治就包括j
   (sum[j] + cnt[j])：u-j,以及j往下的全部的总和不能囊括进up[j]的计算，因此需要删除这一部分；
   n-cnt[j]：u以及上面节点的数量的总和；
 */
void dfs2(int u,int father){
    for(int i=h[u];i!=-1;i=ne[i]){
        int j = e[i];
        if(j==father) continue;
         //因为向上方向的u的节点的信息已经知道了，所以需要先更新j的节点的信息
        up[j] = up[u] +sum[u] - (sum[j]+cnt[j]) + n - cnt[j];
        //然后再递归的往下更新：
        dfs2(j,u);
    }
}

  //需要从下往上和从上往下分别的计算：
   dfs1(0,-1);
   dfs2(0,-1);