BFS图的遍历问题（有向/无向图的邻接表存储形式）

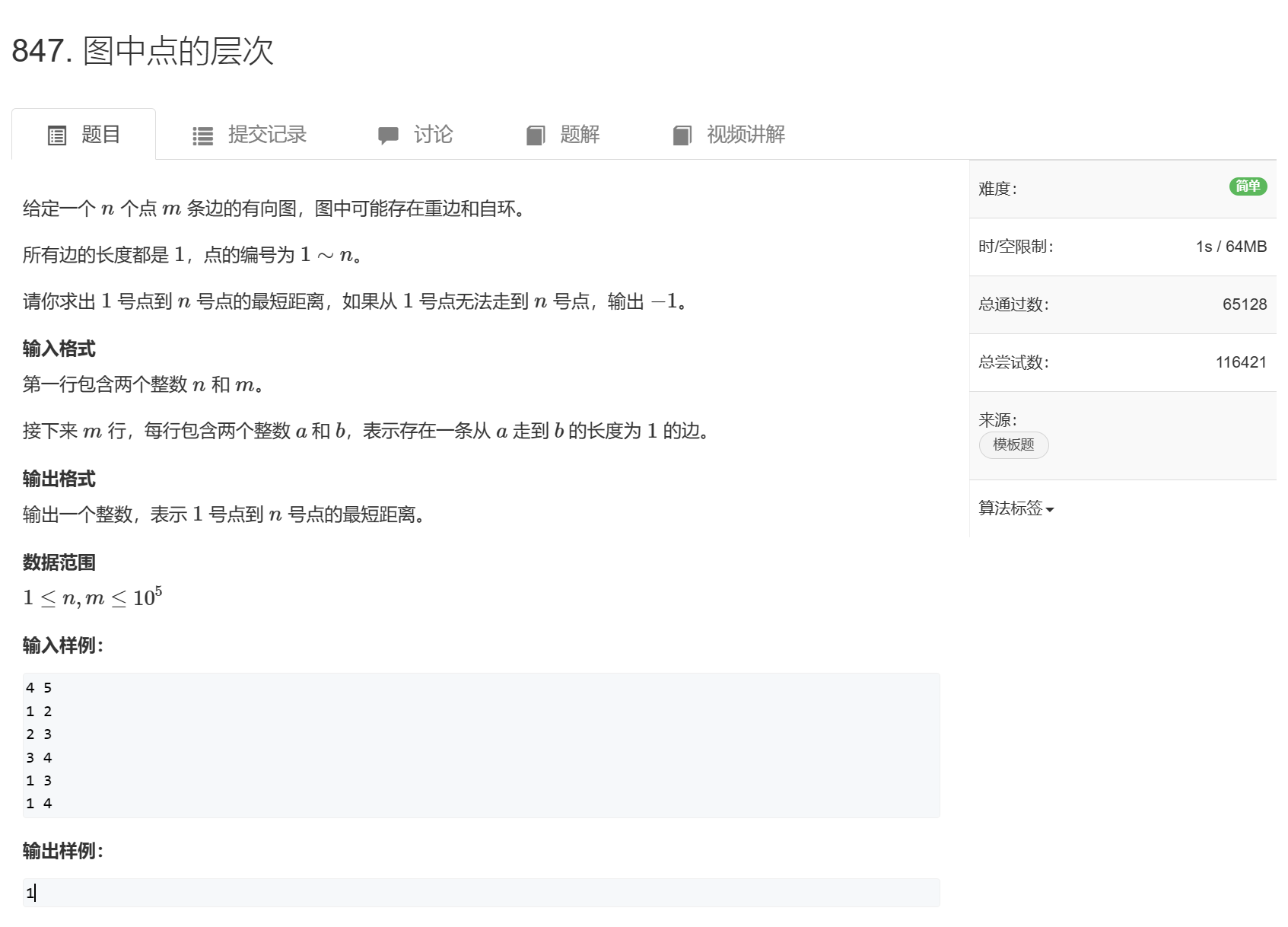
BFS一般解决的问题：两点之间的最短路

BFS问题的模板：

• 创建一个队列，将第一个元素入队
• while循环直到队列为空，在while循环中弹出队列头的元素，判断通过这个元素可以拓展出哪些新的结点，将这些结点入队。
• 在上述过程中找到想要的答案

图的邻接表存储：

• 需要的数据结构为：int h[N], nex[N], e[N], idx;
• h[N]:h[i]为从结点i出去的第一条边（顺序无所谓），这条边在邻接表的链表头 这里的i代表点
• nex[N]: nex[idx]代表下一条起点是i的边, 类比单链表的next，idx是边的编号
• e[N]: e[idx]代表以i为起点，idx这条边的终点的点的序号，表示的是边的终点
• idx:可以理解为边的索引号
• add函数是重点，它的功能是如何向邻接表中添加一条边，传入的参数就是起点a终点b

#include<iostream>
#include<cstring>
#include<queue>

using namespace std;

const int N = 1e5 + 10;
int h[N], nex[N], e[N], idx;
bool st[N];
int n, m;

void add(int a, int b){
    e[idx] = b;
    nex[idx] = h[a];
    h[a] = idx;
    idx++;
}

int bfs(){
    queue<pair<int,int>> q;
    q.push({1, 0});
    st[1] = true;

    while(!q.empty()){
        auto t = q.front();
        q.pop();
        int node = t.first;
        int distance = t.second;
        st[node] = true;
        if(node == n) return distance; //node=n已经代表找到结点1到结点n的最短距离
        for(int i = h[node] ; i != -1 ; i = nex[i]){ //for循环中的i代表的是边
            int j = e[i];
            if(!st[j]){ //只需要将从来未遍历过的点加入队列
                //st[j] = true;
                q.push({j, distance + 1});
            }
        }
    }

    return -1;
}
int main(){
    scanf("%d %d", &n, &m);

    memset(h, -1, sizeof(h));
    for(int i = 0 ; i < m ; i++){
        int a = 0, b = 0;
        scanf("%d %d", &a, &b);
        add(a,b);
        //add(b,a); 若为无向图需要加上
    }

    printf("%d", bfs());
    return 0;
}