状态何时可以转移

• 前一列是1，后一列不能是1，因为会重叠j & k == 0
• 合并列后连续0的个数为偶数st[j | k] == 1

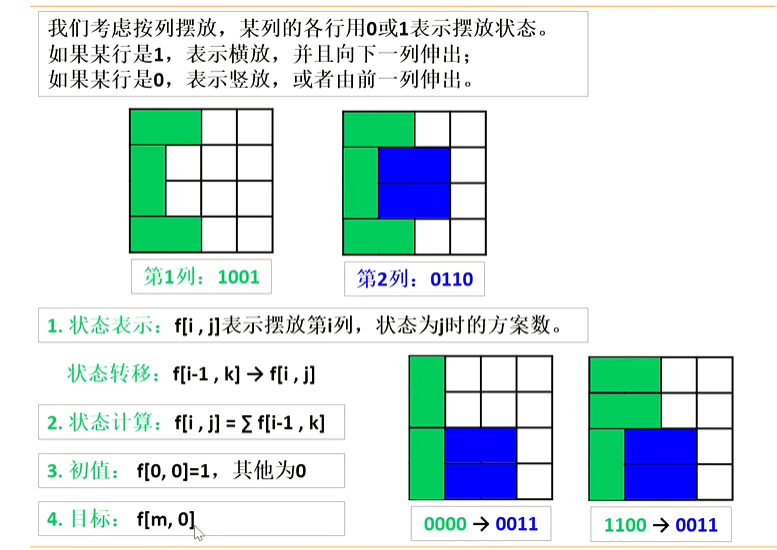
状态计算解读

• 因为f[i][j]表示的是方案数,因此f[i][j] += f[i][k]求的是当前的所有方案
• 目标是f[m][0]:摆放好了最后一列，并且最后一列没有向下一列伸出的格子

AC代码

while 1:
    n, m = map(int, input().split())
    if n == 0 and m == 0:
        break

    # 每一次需要预处理出来所有合法的状态
    # 要判断每个状态是不是合法，需要判断出合并列之后连续0的个数是否为偶数
    st = [True for _ in range(1 << n + 1)]
    for i in range(1 << n):
        cnt = 0
        for j in range(n):
            if i >> j & 1: # 如果当前列为1
                if cnt & 1: # 如果连续0的个数为奇数
                    st[i] = False
                    break
            else:
                cnt += 1
        # 需要额外判断高位是不是存在0
        # 例如4 -> 0100 枚举到1的时候连续0的个数为偶数，本应该继续判断，但是break了，所以需要再加一个判断高位
        if cnt & 1:
            st[i] = False

    f = [[0] * (1 << n + 1) for _ in range(m + 1)]
    f[0][0] = 1
    for i in range(1, m + 1): # 枚举列
        for j in range(1 << n): # 枚举第i列状态
            for k in range(1 << n): # 枚举第i - 1列状态
                if (j & k) == 0 and st[j | k]:
                    f[i][j] += f[i - 1][k]

    print(f[m][0])