算数基本定理

质数性质

任意一个大于1的整数要么本身是质数，要么可以分解为一些质数的乘积。
公式 1：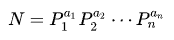
$P_1, P_2, P_3, … , P_n$ 是N的所有质因数。
$a_1, a_2, a_3, … , a_n$ 是质因数对应的指数。

分解质因数

由公式1可得

• x 的质因子最多只包含一个大于 根号x 的质数。如果有两个，这两个因子的乘积就会大于 x，矛盾。

• i 从 2 遍历到 根号x。 用 x / i，如果余数为 0，则 i 是一个质因子。

• s 表示质因子 i 的指数，x /= i 为 0，则 s++， x = x / i 。

• 最后检查是否有大于 根号x 的质因子，如果有，输出。

质数筛

#include "bits/stdc++.h"
#define int long long
using namespace std;
typedef pair<int,int> PII;
const int N = 500010,INF = 0x3f3f3f3f;
int n;
map<int,int> _;
int primes[N], cnt;
bool st[N];

void get_primes(int n) {
    memset(st, false, sizeof st);
    cnt = 0;
    for(int i = 2; i <= n; i++) {
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}

$ primes $ 数组中存的是所有的质数

约数性质

约数个数定理
公式 2：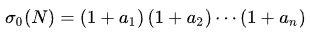
由算数基本定理可得，$a_n$表示质数的指数，而$N$由若干个$P_n$组成，由于$P_n$是质数，它自身只有约数$1$，所以$P_n$的约数个数为$(a_n + 1)$。N又是由若干个这样的$P_n$组成，由此可以推导出以上公式。

约数之和定理
公式 3：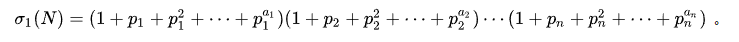
由公式1和公式2易得$P_n$的所有约数之和为$1 + P_n^1 + P_n^2 + … + P_n^a$，由此可推理出公式3。

欧拉函数

n的阶乘分解


我们要先记录一下$ n $的所有质因子,然后按照上面的公式分解即可

#include "bits/stdc++.h"
#define int long long
using namespace std;
const int N = 1e6 + 10;
int n, cnt;
int primes[N];
bool st[N];

void get_primes(int n) {
    memset(st, 0, sizeof st);
    for (int i = 2; i < n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    get_primes(1e6 + 10);
    cin >> n;
    for (int i = 0; i < cnt; i++) {
        int res = 0;
        int p = primes[i];
        for (int j = n; j; j /= p) {
            res += j / p;
        }
        if (res) {
            cout << p << " " << res << '\n';
        }
    }
}