二分,通常用来查找;
普通查找,难免遍历整个数组:O(n)的时间复杂度
但如果是二分,类似于二进制编码的原理,将时间复杂度控制在O(logN),底数是2;

y总总结过:一个题目,如果一个区间具有单调性质,那么一定可以二分,但是如果说这道题目没有单调性质,而是具有某种区间性质的话,我们同样可以使用二分.

划重点:二分的使用通常伴随:单调性,区间性质.但我做完一些题之后,发现只要有区间二段性的,也就是以一个点为分界,左右情况不同,也使用二分;同样,二分的对象是什么,也需要扣题分析

还有呢就是,不要自己限制了自己二分可以取到值的可能性,比如被二分的值全是奇数,那么二分出来的值也可以是非奇数哦!

回过头来看这些模板,模板一是从左边开始找大于等于目标值的值,模板二是从右边开始找大于等于目标值的值,分别近似对应algorithm:lower_bound(找第一个大于等于目标值的值),upper_bound(找第一个大于目标值的值).

算法模板1:

//从左边开始查找:对应的a[mid] >= k ,mid是被夹逼的中值,k是要查找的元素;
void equant(int a[],int k)//待查找元素
{
   int l = 0,r = n - 1;//n是输入数组a[]的长度    //注意!!!数组从0开始,这里的r就取n-1,如果从1开始取,r取n;
    while(l < r)
    {
        int mid = r+l >> 1;//如果mid 赋值给了r,那么mid就不用+1;
        if(a[mid] >= k) r = mid;
        else l = mid + 1;
    }
    if(a[l] != k) {cout << "从前面找,找不到这个元素" << endl;continue;}

    ...;
}

算法模板2:

//从右边开始查找:对应的a[mid] <= k;
void equant(int a[],int k)
{
    int l = 0 , r = n - 1;

    while(l < r)
    {
        int mid = r+l+1 >> 1//如果mid赋值给了l,那么mid就需要+1;
        if(a[mid] <= k) l = mid;
        else r = mid-1;
    }
    if(a[l] != k) {cout << "从后面找,找不到这个元素" << endl; continue;}

    ...;
}

例题1:acwing算法基础课题目:数的范围
相比于基础课里的算法做了一点小小的优化

#include <iostream>

using namespace std;

const int N = 100010;

int a[N];
int n,q,k,l,r;

int main()
{
    cin >> n >> q;

    for(int i = 1 ; i <= n ; i++) cin >> a[i];

    while(q--)
    {
        cin >> k;

        l = 0 , r = n;
        while(l < r)
        {
            int mid = l+r >> 1;
            if(a[mid] >= k) r = mid;
            else l = mid+1;
        }
        if(a[l] != k) {cout << "-1 -1" << endl; continue;}

        cout << l-1 << " ";

        r = n;
        while(l < r) 
        {
            int mid = l+r+1 >> 1;
            if(a[mid] <= k) l = mid;
            else r = mid-1;
        }
        cout << l-1 << endl;
    }
    return 0;
}

例题二:算法基础课:数的三次方根.
一定要注意,最后代码打印的一定要用printf(“%.6f”, );

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int main()
{
    double n; cin >>  n;

    double l = -10010 , r  = 10010;

    while(r - l > 1e-8)
    {
        double mid = (l+r)/2 ;
        if(mid * mid * mid  >= n) r =  mid;
        else l = mid;
    }
    printf("%.6lf",l);
}

例题三:NOI提高组题目:借教室
二分加差分.
二分对订单标号,差分对区间订单要借用的教室数目.

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>

#define int long long

using namespace std;

const int N = 1000010;

int a[N],b[N],sum[N];
int d[N],s[N],t[N];
int n,m;

bool check(int mid)
{
    memset(b,0,sizeof b);
    memset(sum,0,sizeof sum);
    for(int i = 1 ; i <= mid ; i ++) { b[s[i]]+=d[i] ; b[t[i]+1]-=d[i]; }

    for(int i = 1 ; i <= n ; i++) 
    {
        sum[i] = sum[i-1] + b[i];
        if(a[i] < sum[i] ) return false;
    }
    return true;
}

signed main()
{
    cin >> n >> m;

    for(int i = 1; i <= n ; i++) cin >> a[i];

    for(int i = 1 ; i <= m ; i++) cin >> d[i] >> s[i] >> t[i];

    int l = 0 , r = m;

    while(l < r)
    {
        int mid = (l+r+1) >> 1;
        if(check(mid)) l= mid;//执行的话:a[i] > sum[i];
        else r = mid-1;
    }
    if(r == m) puts("0");
    else printf("-1\n%lld\n" , r + 1);//r满足的情况是合理的极限情况.

    return 0;
}

例题四: 蓝桥题目:分巧克力
这道题在对l和r的评判上出错了
如果刚开始我l取0,而对r我是这样赋值的

for (int i = 0; i < n; i ++ ) 
    {
        scanf("%d%d", &h[i], &w[i]);
        minnum = min(h[i] , minnum);
        minnum = min(w[i] , minnum);
    }

这是前面的代码,我取可能的巧克力的最小边长对r赋值.
结果这样我试了,最多,撑死只能过3个样例.服了.我还以为这样简化了代码~笑死

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>

#define int long long

using namespace std;

const int N = 100010;

int n,k,minnum  = 1e5 + 10;
int h[N],w[N];

bool check(int mid)//1表示 > k;  0 表示圆满; -1表示 < k; 
//切完的蛋糕数目应该 >= k的临界值;另一种情况是<k,不够肯定不行啊!!!
{//下取整
    int len = 0 , wide = 0;
    int sum = 0;

    for(int i = 1 ; i <= n ; i++) 
    {
        len = h[i] / mid;//3
        wide = w[i] / mid;//2
        sum+= len * wide;
        if(sum >= k) return true;
    }
    return false;
    /*if(sum < k) return -1;//不满足要求,再小点!!!
    else  return 1;*/

}

signed main()//暴力 : 1e10;  二分优化:log(1e10);
{
    cin >> n >> k;

    for(int i  = 1 ; i  <= n ; i++) cin >>  h[i] >> w[i];
    //cout << minnum << endl;

    int l = 0 , r = 1e5;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(check(mid)) l =  mid;//小了;
        else  r = mid -1;
    }


    cout << r << endl;

    return 0;
}

例题五:蓝桥赛题:管道
没什么好说的,第一遍check函数完全写错了,但就是有思路,代码转化能力的问题
这道题和算基课里面的区间合并那道题难度高一点,区间需要自己去取
其他没有一丝一毫的变化.就看你会不会取区间了
或者说这道题的难点就在取区间.

区间该如何取呢?根据你所二分查找的结束时刻来,很简单的数学,画个数轴一目了然

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

#define int long long

typedef pair<int,int> PII;

#define x first
#define y second

const int N = 100010;

PII w[N],s[N];
int n,m;

bool check(int mid)
{
    int cnt = 0;
    for(int i = 0 ; i < n ; i++)
    {
        int p = w[i].x , t = w[i].y;
        if(mid >= t)
        {
            int der = mid - t;
            int l = max(w[i].x - der, (long long)1), r = min(m , w[i].x + der);
            s[cnt++] = {l,r};
        }
    }

    sort(s,s+cnt);

    int st = -1, ed = -1;
    for(int i = 0 ; i < cnt ; i ++)
    {
        if(ed + 1 >= s[i].x) ed = max(ed,s[i].y);
        else st = s[i].x , ed = s[i].y;
    }

    return st==1 && ed==m;
}

signed main()
{
    cin >> n >> m;

    for(int i  = 0 ; i < n ; i++) scanf("%lld%lld",&w[i].x,&w[i].y);

    int l = 0, r = 2e9;
    while(l < r)
    {
        int mid = (l + r ) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }

    cout <<  l << endl;

    return 0;
}

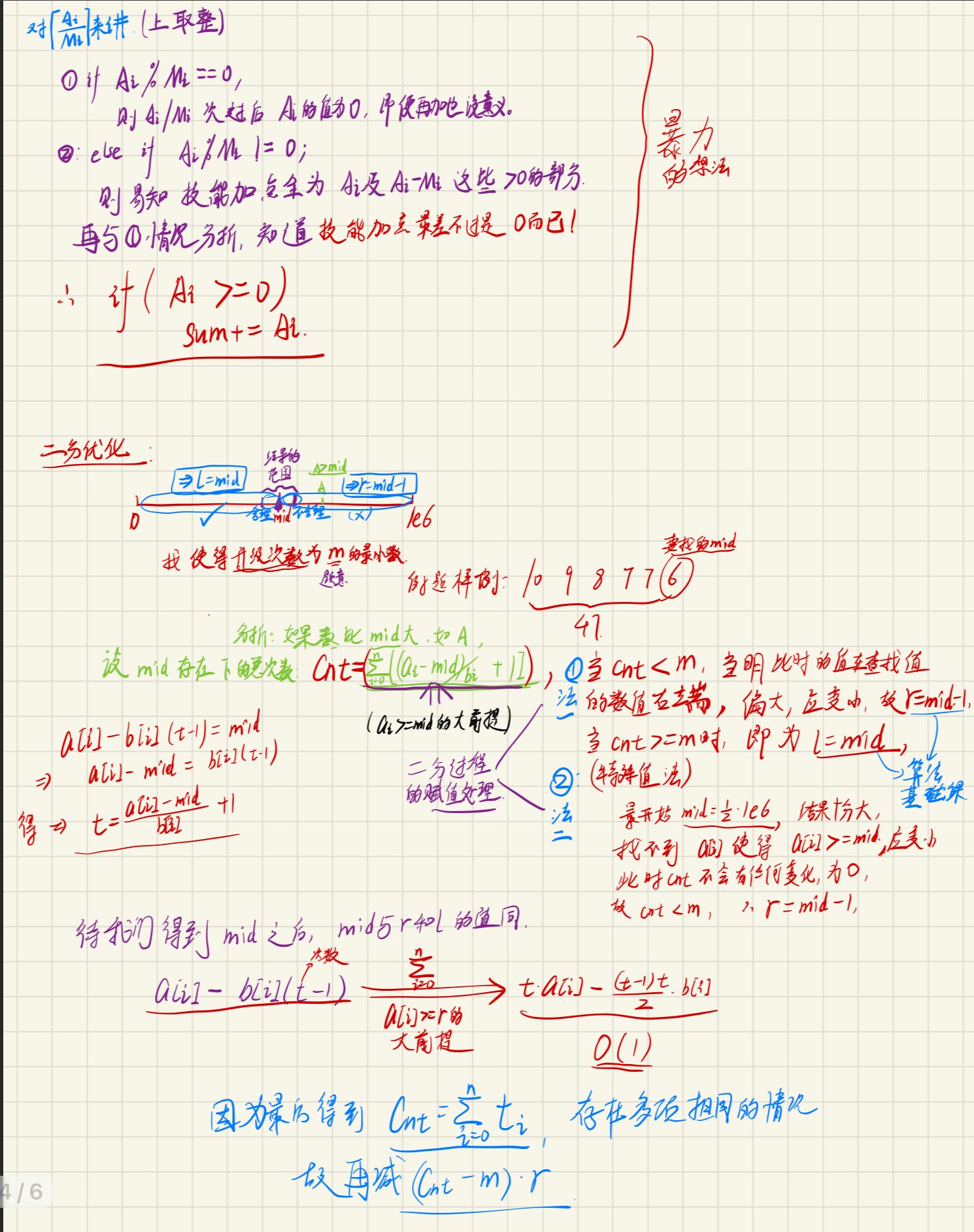
例题六:蓝桥第十三届赛题:技能提升

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
#define int long long

const int N = 100010;

int a[N],b[N];
int n,m;

bool check(int mid)
{
    int cnt = 0;
    for(int i = 0 ; i < n ; i ++)
    {
        if(a[i] >= mid)
            cnt += (a[i] - mid) / b[i] + 1;
    }
    return cnt >= m;
}

signed main()
{
    cin >> n >> m;

    for(int i = 0 ; i < n ; i++) scanf("%lld%lld",&a[i],&b[i]);

    int l = 0 , r = 1e6;
    while(l < r)
    {
        int mid = (l + r + 1 )>> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }

    int res = 0 , cnt = 0;
    for(int i = 0 ; i < n ; i++)
    {
        if(a[i] >= r)
        {
            int t = (a[i] - r)/b[i] + 1;
            cnt += t;
            res += t*a[i] - (t-1)*t*b[i]/2;
        }
    }
    cout << res - (cnt - m)*r << endl;
}

洛谷P1102题

https://www.luogu.com.cn/problem/P1102#submit

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
#define int long long
const int N = 1e6 + 10;
typedef pair<int, int> pii;
int a[N], b[N], n, c;
map<string, int> mp;//string代表的是字符串序号的直接相加
void Lntano()
{//说真的,又被自己蠢哭
    //题目中有两个数组的数相减,得到的答案是C,但是为什么要处理两个变量增大出错的概率呢???
    int cnt = 0;
    for (int i = 0; i < n; i++)
    {
        int num1 = 0, num2 = 0;
        int k = a[i] - c;
        int l = 0, r = n - 1;
        while (l < r)//感觉自己曲解了二分的意思,最后要的是l,r
        {
            int mid = (l + r) >> 1;
            if (a[mid] >= k) r = mid;
            else l = mid + 1;
        }
        num1 = l;//找的是从左边开始大于等于k的最大值.
        if (a[num1] != k) continue;
        //cout << num1 << " ";
        l = 0, r = n - 1;
        while (l < r)
        {
            int mid = (r + l + 1) >> 1;
            if (a[mid] <= k) l = mid;
            else r = mid - 1;
        }
        num2 = l;//从右边开始大于等于k的最大值.
        //cout << num2 << "\n";
        cnt += num2 - num1  + 1;
    }
    if (c == 0) cnt--;
    cout << cnt << "\n";
}
signed main()
{
    cin >> n >> c;
    for (int i = 0; i < n; i++) cin >> a[i];
    sort(a, a + n);
    Lntano();
    return 0;
}

因为y总的模板一与模板二可以近似看成lower_bound()与upper_bound()函数,所以另一个AC的代码如下:

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <vector>
#include <map>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int, int> pii;
#define int long long
int a[N], n, c;
map<string, int> mp;//string代表的是字符串序号的直接相加
void Lntano()
{
    int ans = 0;
    for (int i = 0; i < n; i++)
    {
        int k = a[i] - c;
        int x1 = upper_bound(a,a+n,k) - lower_bound(a, a + n, k) ;
        ans += x1;
    }
    if (c == 0) ans--;
    cout << ans << endl;
}
signed main()
{
    cin >> n >> c;
    for (int i = 0; i < n; i++) cin >> a[i];
    sort(a, a + n);
    Lntano();
    return 0;
}