回溯算法

• 回溯算法中函数返回值一般为void。

• 回溯函数终止条件:

if (终止条件) {
    存放结果;
    return;
}

• 回溯搜索的遍历过程:，回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。
  

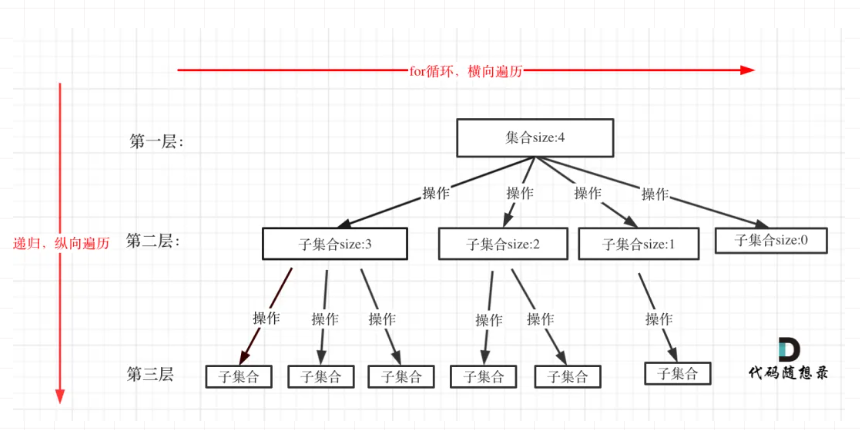
图中，特意举例集合大小和孩子的数量是相等的！

回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

可以从图中看出「for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历」，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

 void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

gpt给出的模板：

def backtrack(candidate, state):
    if state is terminal:
        # 判断是否为最终解，如果是则返回解
        output(candidate)
        return

    for next_candidate in list_of_candidates:
        if is_valid(next_candidate, state):
            # 如果满足约束条件，进行选择
            choose(next_candidate, state)
            # 递归调用回溯函数
            backtrack(next_candidate, state)
            # 撤销选择，进行回溯
            unchoose(next_candidate, state)

def is_valid(candidate, state):
    # 判断当前状态下的候选解是否满足约束条件
    pass

def choose(candidate, state):
    # 根据候选解，做出选择，更新状态
    pass

def unchoose(candidate, state):
    # 撤销上一步的选择，恢复到之前的状态
    pass

def output(candidate):
    # 输出结果，这里根据具体问题自定义
    pass

# 初始化调用
backtrack(initial_candidate, initial_state)

来源：代码随想录