堆(下标从1开始)

堆是一个完全二叉树：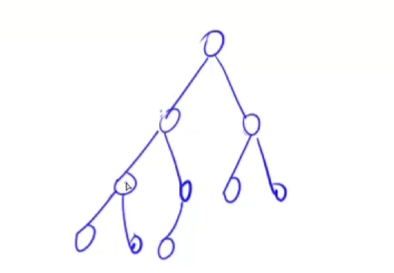

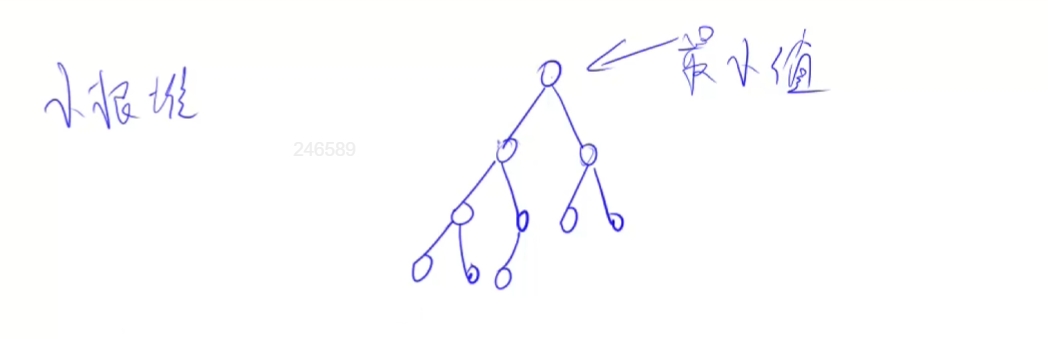
小根堆

根节点是最小值，小于他的左右节点

堆的存储

使用一维数组存储

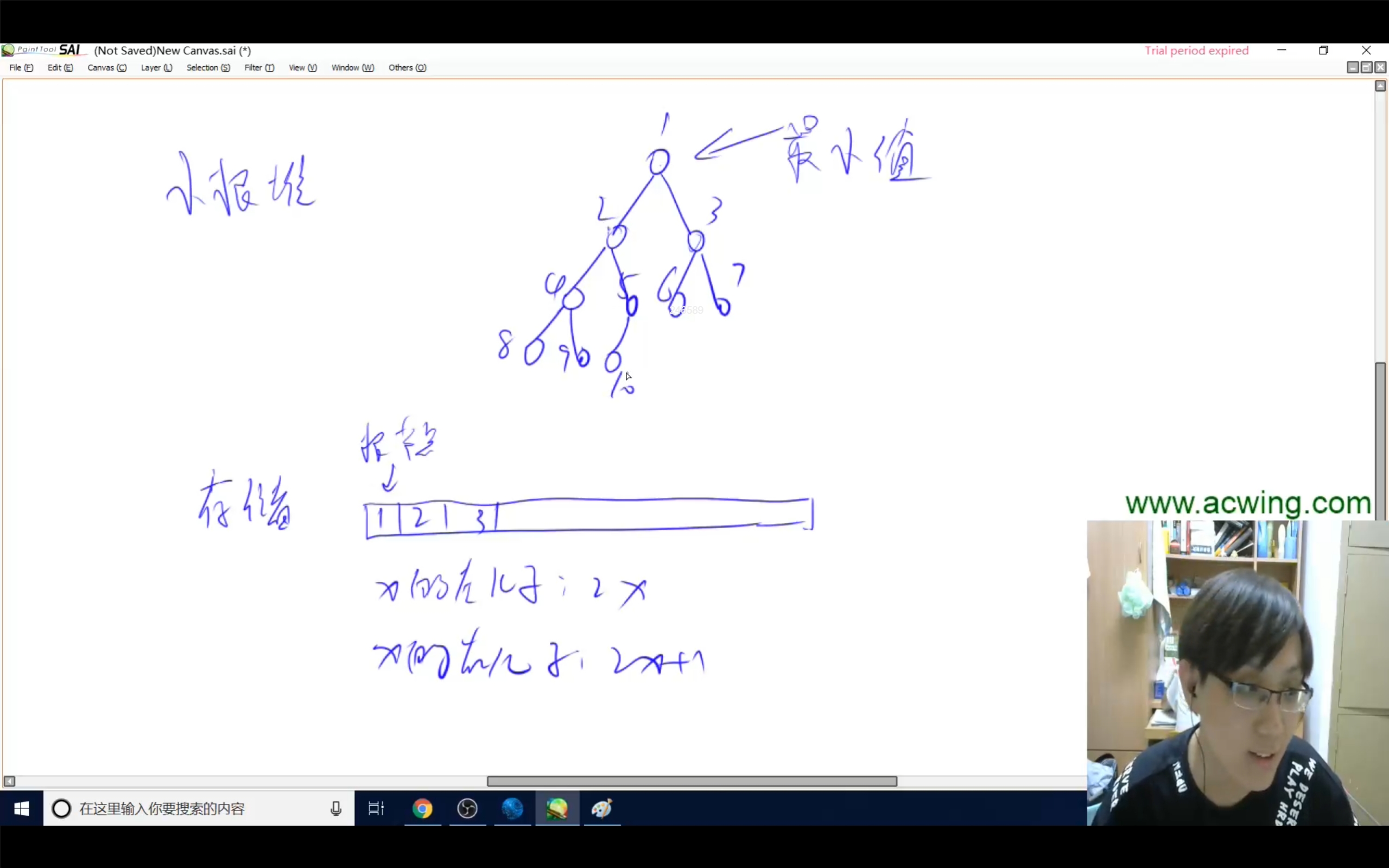
小根堆的down()操作

例如，现在有小根堆：
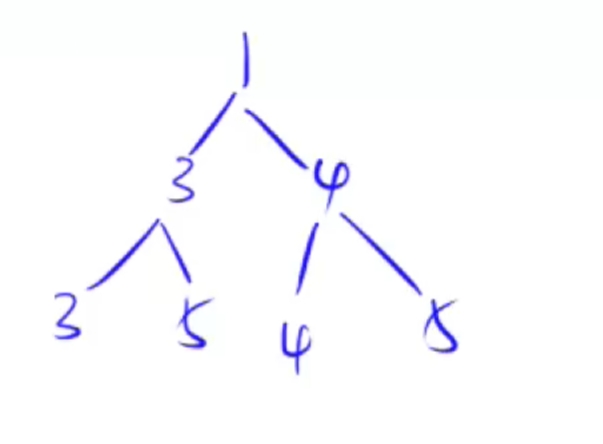
将根节点换成6，有：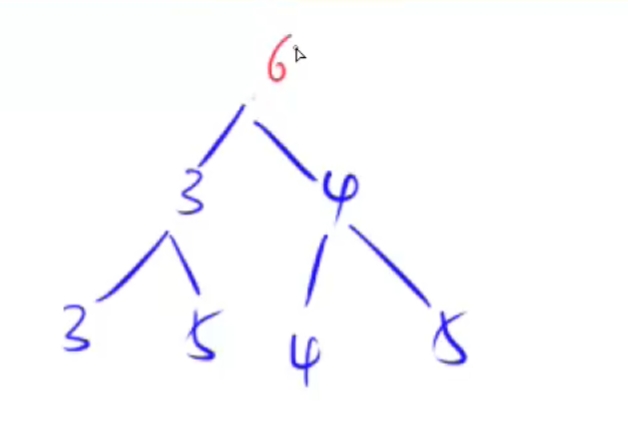
因为此时不满足小根堆的定义，所以6要不断下沉，即down();


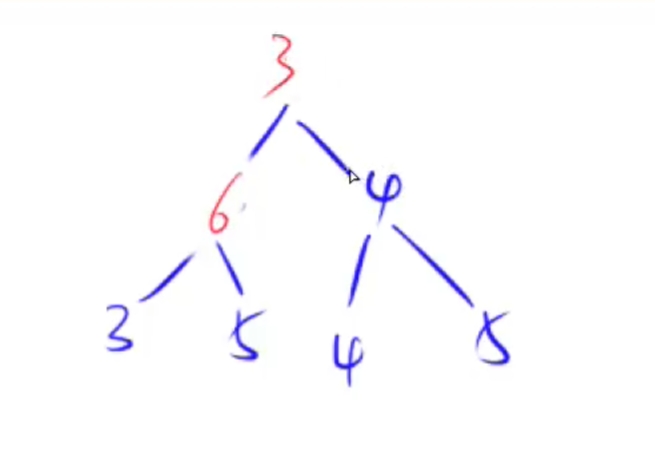
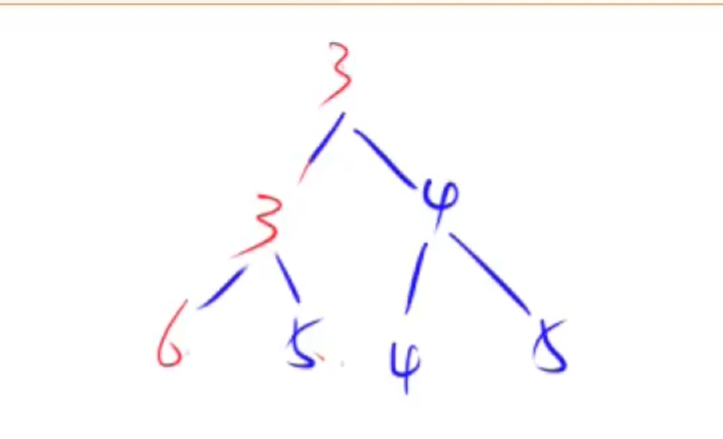
代码为：

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

小根堆的up()操作

当一个节点变小的时候，就要往上走，所以有up()；

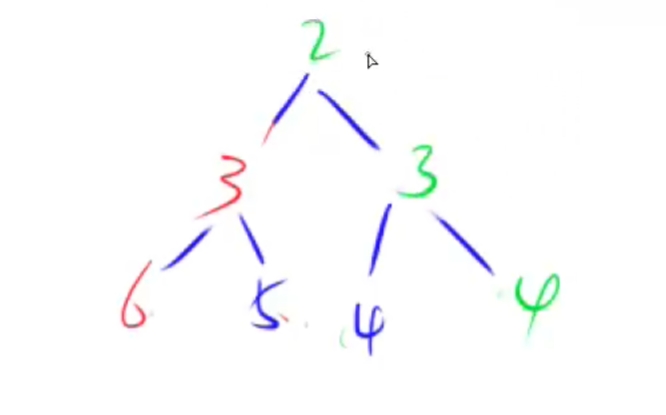
代码为:

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(u, u / 2);
        u >>= 1;
    }
}

小根堆的操作：

1、插入一个数
插入一个新的数，就是在堆的最后一位加上一个新的数，
再不断往上移即可，有：

heap[++size] = x; up(size);

2、求集合中的最小值
显然，小根堆的最小值就是根节点，即heap[1];

3、删除最小值
删除最小值时，把最后一位元素，覆盖掉根节点，最后再down()即可。
因为小根堆的存储是 一位数组，因此将好操作的最后一个点覆盖第一个点即可。

heap[1] = heap[size]; size--; down(1);

4、删除任意一个元素

heap[k] = heap[1]; size--;down(k);up(k);

删除这个元素后，不论后来是down() or up()，依据条件，只会执行一个，所以写在一起，就不用判断
到底是小了，还是大了。

5、修改任意一个元素

heap[k] = x;down(k);up(k);