最短路问题

一、分类

如图：

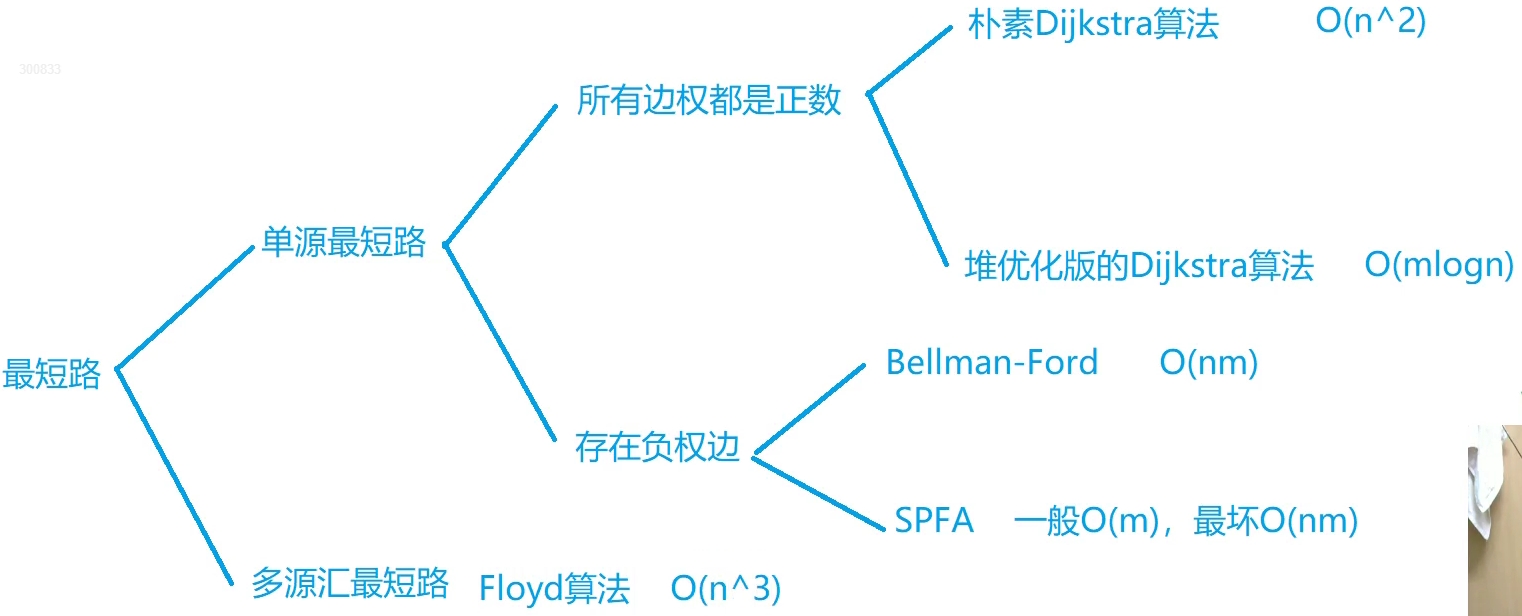
解析：

1.源点 就是 起点，汇点 就是 终点。多源汇就是任给两个点a、b，求他们之间的最短路。
2.约定n代表点数，m代表边数。
3.一些解释：

• 朴素版Dijkstra算法的时间复杂的为O(n²)，与边数m无关，所以适用于稠密图（边多的）。当边数m和O(n²)是一个级别的时候，如果使用堆优化版Dijkstra算法，时间复杂度就会变为O(n²logn)，比朴素高。
• 但如果是稀疏图，比如n和m都是10^5左右的级别，就不能用朴素版，要用堆优化版。
• 稠密图：m和n²一个级别，边多。
• 稀疏图：m和n一个级别，边少。

4.SPFA算法是对Bellman-Ford算法的优化。但如果对最短路经过的边数有限制的话，那么就只能使用Bellman-Ford算法。
5.原理（这个不要求掌握）
Dijkstra算法基于贪心，Floyd算法基于动态规划，Bellman-Ford算法基于离散数学的一些知识。
6.最短路算法只需要考虑有向图，因为无向图是特殊的有向图。
7.正权图建议使用Dijkstra，负权的话SPFA比较好用。但y总本人很推荐SPFA算法，很多正权图的问题拿SPFA都可以过，但如果被卡了就要换。（被卡的意思就是出题人将SPFA算法的时间复杂度卡到了O(nm)，此时就需要使用堆优化版的Dijkstra算法）

二、难点

1.最短路问题的难点在于：建图，即如将原问题抽象为最短路问题，如何定义出点和边。

三、解析

1. 为什么Dijkstra算法求最短路时，要求图中不能有负权边？

ChatGPT：
Dijkstra算法是一种用于在加权图中找到某个顶点到其他所有顶点的最短路径的算法。其基本原理是每次从未确定最短路径的顶点中选择一个距离最小的顶点，然后通过这个顶点更新其他顶点的最短路径。这个过程依赖于一个关键的假设：一旦顶点的最短路径被确定，它就不会再改变。

这里的假设建立在所有边的权重都是非负的基础上。如果图中存在负权边，这个假设就不再成立，因为：

• 当图中包含负权边时，一个顶点的最短路径可能会因为后续的计算而发生变化。具体来说，如果通过已确定最短路径的顶点可以回溯到一条包含负权边的路径，那么这条路径可能比之前找到的路径更短。
• 这意味着，当算法选择了一个顶点作为最短路径确定的顶点后，由于负权边的存在，可能会出现通过这个顶点回溯并包含负权边的路径，使得原本确定的最短路径变得不再是最短的。
• Dijkstra算法的每一步选择都是基于当前已知的最短路径来更新其他顶点的距离，如果存在负权边，那么这个基于局部最优选择的过程就不能保证得到全局最优解，因为它没有回溯重新考虑之前的选择。

简而言之，Dijkstra算法在设计时假定通过增加更多的边可以使路径的总权重增加，这对于非负权重是成立的。但是，如果存在负权边，这个假定就不成立了，可能会出现通过增加边使得路径总权重减少的情况，这就违反了Dijkstra算法的基本原理。

对于包含负权边的图，Bellman-Ford算法或者Floyd-Warshall算法就可以用来找到最短路径，因为它们能够正确处理负权边的情况。