双指针—6题20图一次搞懂

使用双指针是降低算法复杂度的一个有效途径，有些问题的暴力解法时间复杂度是O(n^2)，但使用双指针可以大幅度降低算法复杂度。如果面试者能将求解过程从暴力法优化到双指针，说明面试者的基础知识、代码能力、逻辑思维都是十分扎实的。

同贪心算法一样，双指针的难点在于自己想不出、别人的理解不了、正确性难以证明。

常用的双指针法有一下几类：

1. 左右指针：两个指针，相向而走，中间相遇。

2. 快慢指针：两个指针，有快有慢，同向而行。

3. 灵活运用：两个指针，灵活运用，伺机而动。

下面将结合具体题目，从暴力做法一步一步优化到双指针，攻克想不出、看不懂、不会用的难题。

左右指针

左右指针地熟练使用需要一定经验的积累，如果接触的较少，是不容易想出来的。下面将以题目为例，一步步从暴力解法优化到双指针。

思路：先找出暴力解法，根据题目性质，优化到双指针

例题一:盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点(i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为(i, ai)和(i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

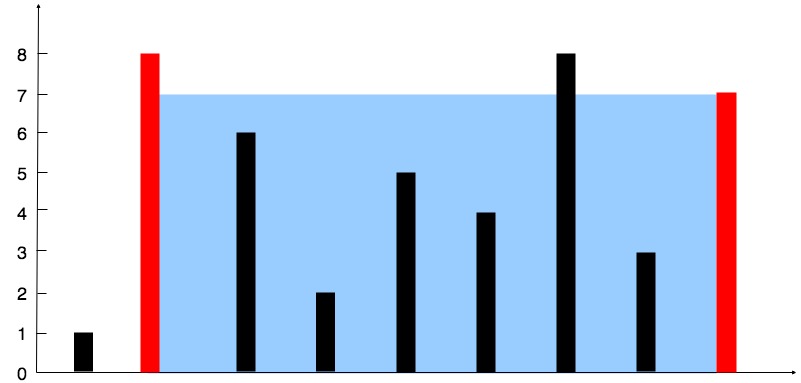
示例 ：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

这道题的最优解法是左右双指针法。双指针法的难点在于难于想到，难以证明。接下来将一步一步地从暴力解法优化到双指针法。证明也就很简单了。

暴力法：

找出每一种情况，求出盛水值，最大的就是答案。

1. i指向左挡板，从第一块到遍历倒数第二块。

2. j指向右挡板，从倒数第一块遍历到i后面那一块。

3. res保存最大盛水值。

4. 返回res。

代码：

//cpp
class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size() <= 1) return 0;
        int res = 0;//保存结果
        for(int i = 0; i < height.size() - 1; i++)//以i为左挡板，从O开始
        {
            for(int j = height.size() - 1; j > i; j--)//以j为右挡板，从height.size() - 1开始
            {
                int L = j - i;//底边长度
                int H = min(height[i], height[j]);//对短的挡板为高
                res = max(res, L * H);//取最大值
            }
        }
        return res;
    }
};

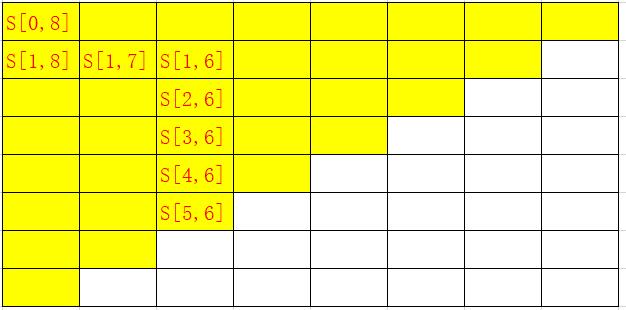
用S[l,r]表示以第l块板为左挡板，第r块板为右挡板的盛水值。S[l, r]就等于min(height[l], height[r]) / (r - l)。

以输入[1,8,6,2,5,4,8,3,7]为例，共8块挡板，看看都计算了哪些值：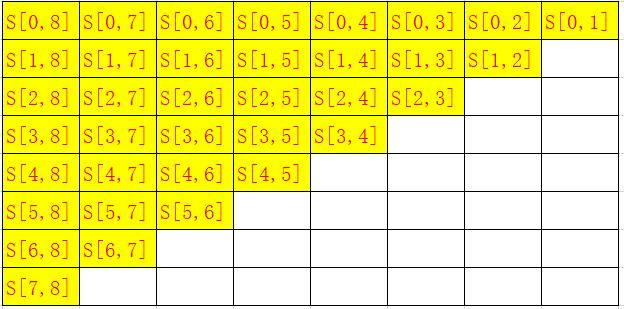

优化：

1. 开始时，l指向第0块挡板，r指最后一块挡板。S[l, r]=min(1, 7) * (8 - 0) = 8。

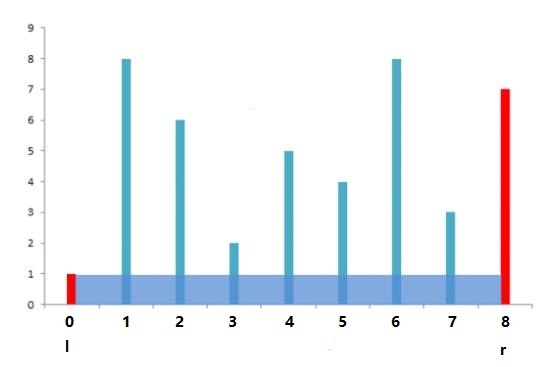
2. 向内移动指向较长挡板的r指针，盛水面积不会变大。向内移动r指针的时候，盛水值S[l, r] = min(height[l], height[r]) / (r - l)。min(height[l], height[r]) 不会大于height[l]，也就是不会大于7。(r - l)会随着r内移减小。所以向内移动r指针的时候,盛水值不可能变大。也就是S[0,8]肯定大于S[0,7],S[0,6],S[0,5],S[0,4],S[0,3],S[0,2],S[0,1]。

因此知道了以height[0]为左挡板的最大盛水值。以后计算就不用考虑height[0]了

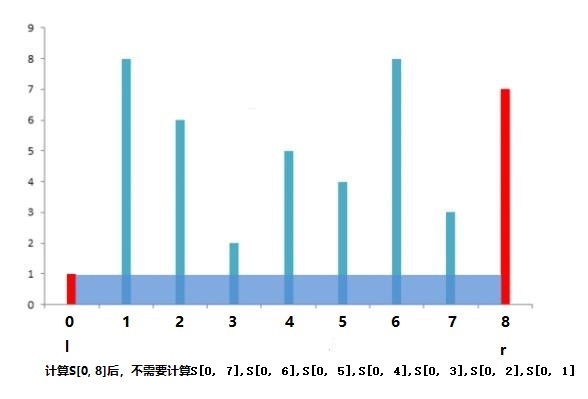
3. 子问题就变成了：在[8,6,2,5,4,8,3,7]中求出最大盛水值，然后与刚才的求出的以height[0]为左挡板的最大盛水值比较大小，大的为答案。

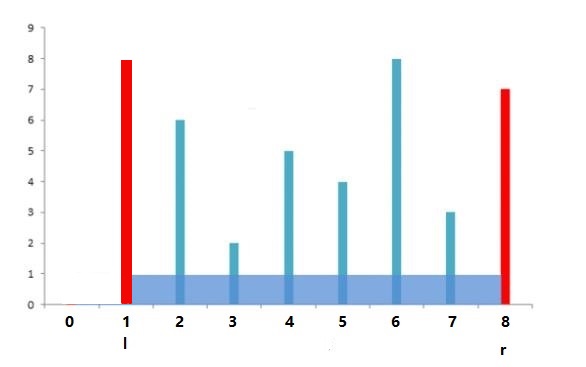
4. 子问题求解时，用l指向指向第0块挡板，也就是height[1]，r指最后一块挡板,也就是height[8]。S[l, r]=min(8, 7) / (8 - 1) = 56。

这个时候，如果向内移动指向较长挡板的l指针，盛水面积不会变大。

因为向内移动l指针的时候，盛水值S[l, r] = min(height[l], height[r]) / (r - l)。min(height[l], height[r]) 不会大于height[r]，也就是不会大于7。(r - l)会随着l内移减小。所以向内移动l指针的时候,盛水值不可能变大。也就是S[1,8]肯定大于S[2,8],S[3,8],S[4,8],S[5,8],S[6,8],S[7,8]，就知道了以height[8]为右挡板的最大盛水值。

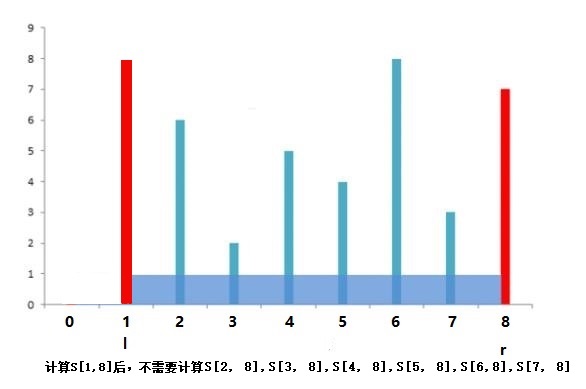
5. 子问题可以再次缩小，就变成了：在[8,6,2,5,4,8,3]中求出最大盛水值，然后与刚才的求出的以height[0]为左挡板的最大盛水值，以height[8]为右挡板的最大盛水值比较大小，大的为答案。

6. 以此类推，每次就能求出以最外侧两个挡板中，短的挡板为边界的最大值。然后再一次缩小问题。就不需要计算所有的情况了，只需要计算出每块挡板为边界的最大值，然后求出其中的最大值，就是答案。

7. 这样下去，求解空间就变为了：

代码:

//cpp
class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size() <= 1) return 0;
        int res = 0;//保存答案
        int l = 0, r = height.size() - 1;//开始时，l指向最左边的挡板，r指向最右边的挡板
        while(l < r)//如果l,r之间还有挡板
        {
            res = max(min(height[l], height[r]) * (r - l), res);//计算盛水值
            if(height[l] <= height [r])//谁小谁以后就不用再考虑 
                l++;
            else
                r--;
        }
        return res;
    }
};

时间上，l,r指针遍历一遍，所以时间复杂度是O(n)。空间上，没有开辟与输入有关的空间，所以空间复杂度是O(1)。

例题二： 和为s的两个数字

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

示例 ：

输入：nums = [2,7,11,15], target = 9
输出：[2,7] 或者 [7,2]

暴力法：

穷举出每一种情况，如果两数之和等于target的，输出答案。

1. i指向数对的第一个数字，从0到nums.size() - 2;

2. j指向数对的第二个数字，从nums.size() - 1到i+1;

3. 如果nums[i] + nums[j] == target，返回[nums[i], nums[j]]

代码：

//cpp
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        for(int i = 0; i < nums.size() - 2; i++)//i指向数对的第一个数字，从0到nums.size()-2
        {
            for(int j = nums.size() - 1; j > i; j--)//j指向数对的第二个数字，从nums.size()-1到i+1
            {
                if(nums[i] + nums[j] == target)//如果两数之和等于target
                    return vector<int>{nums[i], nums[j]};//返回数对
            }
        }
        return vector<int>{-1, -1};//穷举完没有答案，返回[-1,-1]
    }
};

两个遍历数组的循环，所以时间复杂度是O(n^2)；没有开辟与数组大小相关的空间，所以空间复杂度是O(1)

优化一：j不用走到i+1再结束

暴力法没有用到数组有序这个条件，第一次优化利用了数组有序这个性质。

因为数组有序，所以nums[j] > nums[j-1]。若nums[i] + nums[j] < target，则nums[i]加nums[j-1]后面的数一定小于target。所以j不用从nums.size()-1遍历到i+1，只需要遍历到nums[i] + nums[j] < target即可。

举例：nums = [1,4,6,7,8,11]，target = 10。

第一次遍历：i = 0, j = 5开始，当 j减小为4的时候，nums[0] + nums[4] = 1 + 8 = 9 < target。

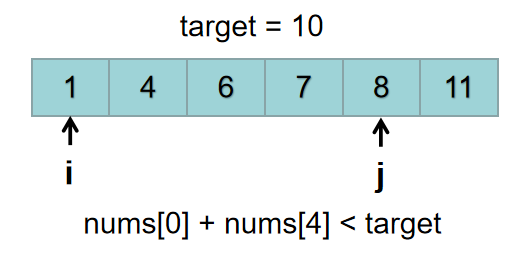
数组有序，所以nums[2] < nums[3] < nums[4]。j往前走，nums[j]的值会一直变小，nums[i] + nums[j]一定小于target。所以j的这次循环可以停止了。

代码

//cpp
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        for(int i = 0; i < nums.size() - 2; i++)//i指向数对的第一个数字，从0到nums.size()-2
        {
            for(int j = nums.size() - 1; j > i; j--)//j指向数对的第二个数字，从nums.size()-1到i+1
            {
                if(nums[i] + nums[j] == target)//如果两数之和等于target
                    return vector<int>{nums[i], nums[j]};//返回数对
                if(nums[i] + nums[j] < target)//当两数之和小于target的时候，nums[j]左侧的数字加nums[i]一定小于target，可以跳出循环。
                    break;
            }
        }
        return vector<int>{-1, -1};//穷举完没有答案，返回[-1,-1]
    }
};

虽然能提前跳出j的循环，但是时间复杂度和空间复杂度都没有变。

优化二：j不用每次都从nums.size()-1出开始

数组有序，所以nums[i + 1] > nums[i]。 如果nums[i] + nums[j] > target, 则nums[i + 1] + nums[j]一定大于target。

程序执行过程中，当第一次遇到nums[i] + nums[j] < target 的时候，j的这次遍历结束。此时，nums[i] + nums[j + 1]是大于target的。

程序执行i + 1,i指向后一个元素，此时，nums[i] + nums[j + 1]肯定大于target。所以j不用从nums.size() - 1重新开始遍历，只需要从当前位置往前遍历即可。

举例：nums = [1,4,6,7,8,11],target = 10。

第一次遍历：i = 0,j = 5开始，当j 为5的时候，nums[0] + nums[5] = 1 + 11 = 12 > target。j向左移动一格后，j = 4。

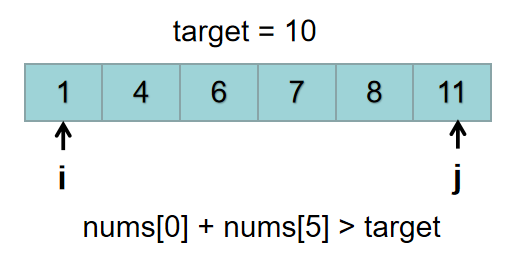
当j为4的时候，nums[0] + nums[4] = 1 + 8 = 9 < target。j的此次遍历结束。这个时候，nums[i] + nums[j] < target, nums[i] + nums[j + 1] > target。

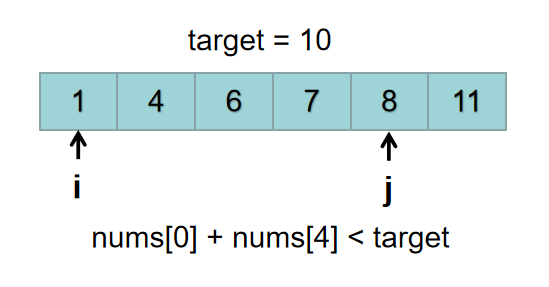
程序继续，执行i+1:i = 1。 数组有序，所以nums[1] > nums[0]。 因为nums[0] + nums[5] > target, 所以nums[1] + nums[5]肯定大于target，所以j不用从5开始往后遍历，从上次位置继续往后遍历即可。

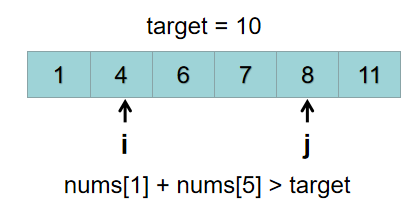
//cpp
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int j = nums.size() - 1;
        for(int i = 0; i < nums.size() - 2; i++)////i指向数对的第一个数字，从0到nums.size()-2
        {
            while(nums[i] + nums[j] > target)//j一直往前走即可
                j--;
            if(nums[i] + nums[j] == target)
                return vector<int>{nums[i], nums[j]};
        }
        return vector<int>{-1, -1};
    }
};

在i从0到nums.size() - 2过程中，j只遍历了一次，所以时间复杂度O(n)；没有开辟与数组大小相关的空间，所以空间复杂度是O(1)。

小结

左右双指针法的实质是合理利用题目的规则，减少遍历的次数，从而降低时间复杂度。可以从暴力出发，想办法利用题目规则，一步一步进行优化。

快慢指针

快慢指针是指移动的步长，即每次向前移动速度的快慢。（例如，让快指针每次前移动2步，慢指针每次向前移动1步）。常被用来在O(N)时间复杂度O(1)空间复杂度的情况下。

例题一： 链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 ：

输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。

暴力法：

1. 用一个指针遍历一遍链表，求出链表的最后一个节点编号:n（节点编号从0开始）。

2. 中间节点在第n/2向上取整的位置。

3. 用一个指针从表头往后走n/2向上取整步，指向的节点就是答案。

//cpp
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        if(!head) return NULL;
        int n = 0;//保存节点编号
        ListNode *p = head;
        while(p->next)
        {
            n ++;
            p = p->next;
        }

        int mid = (n + 1 ) / 2;//中间节点位置。(len + 1 ) / 2 = len/2 向上取整。
        p = head;
        while(mid -- )//走mid步及为中点
        {
            p = p->next;
        }
        return p;
    }
};

时间上遍历两遍链表，所以时间复杂度是O(2n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。

优化：快慢指针法

想象两个人比赛跑步，一个人的速度是另一个人的2倍，当速度快的到达终点的时候，速度慢的人肯定在赛道中点。

同理：用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步，fast 一次走两步。当 fast 到达链表的末尾时，slow 必然位于中间。

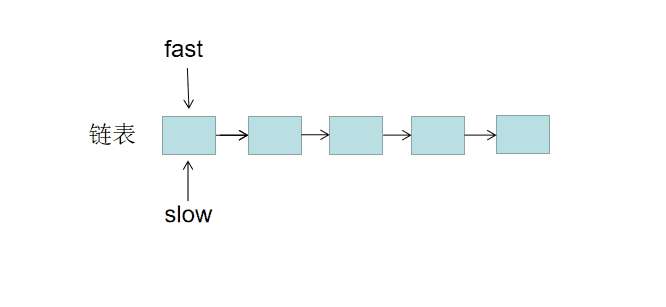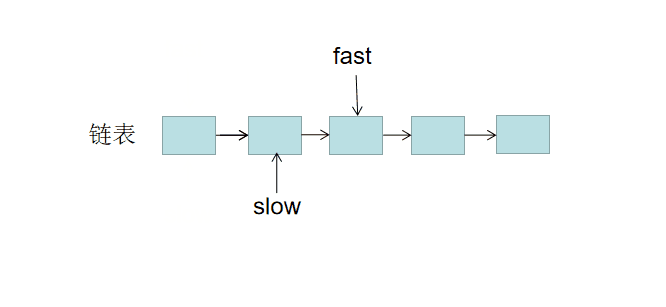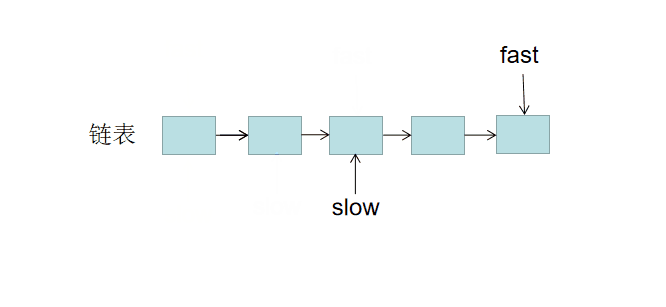
//cpp
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
       if(!head) return NULL;
       ListNode *fast, *slow;
       fast = head;
       slow = head;
       while(fast->next)
       {
           fast = fast->next;
           if(fast->next) fast = fast->next;//fast走两步
           slow = slow->next;//slow走一步
       }
       return slow;
    }
};

时间上遍历一遍链表，所以时间复杂度是O(n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。

例题二：环形链表

暴力法：

遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过。

具体地，使用哈希表来存储所有已经访问过的节点。每次到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。重复这一过程，直到遍历完整个链表即可。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> h;//保存访问过的节点
        while (head != nullptr) {
            if (h.count(head)) {//如果当前访问节点在h中，则有换
                return true;
            }
            h.insert(head);//将当前节点放入h
            head = head->next;
        }
        return false;
    }
};

时间上遍历一遍链表，所以时间复杂度是O(n)；开辟了存储访问过的节点的哈希表，与链表线性相关，所以空间复杂度是O(n)。

优化：

想像两个人从宿舍同时出发去操场跑步，一个人的速度快，一个人的速度慢。经过一段时间后，这两个人总能在操场相遇。

同理：

指针fast，slow在链表上移动，fast移动地快，slow移动地慢。当fast和slow从链表上的同一个节点开始移动时，如果该链表中没有环，那么fast将一直处于slow 的前方；如果该链表中有环，那么fast会先于slow 进入环，并且一直在环内移动。等到slow 进入环时，由于fast的速度快，它一定会在某个时刻与slow相遇。

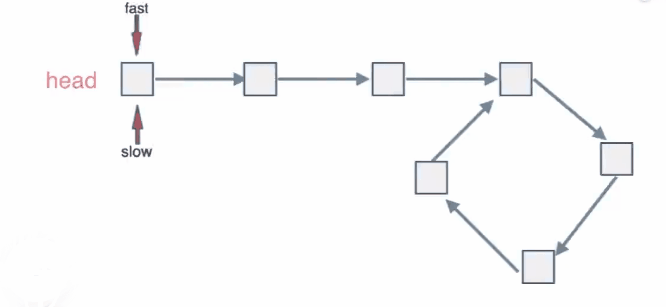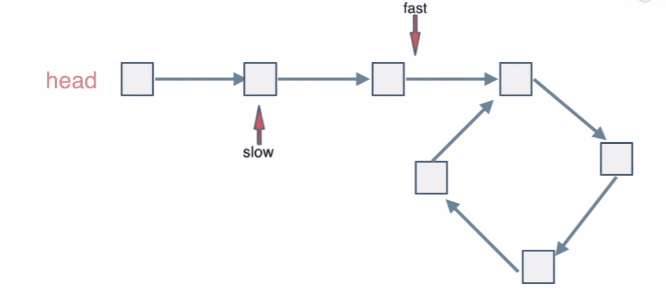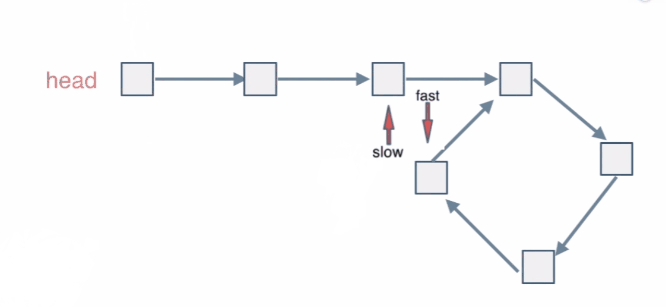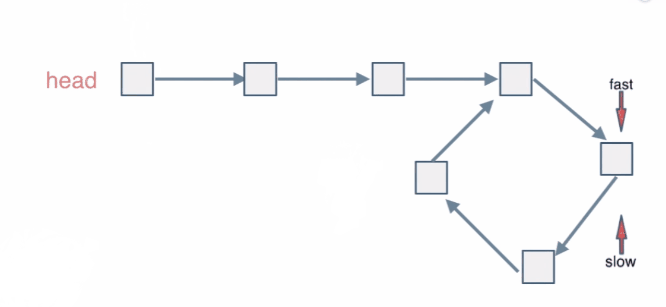
class Solution {
public:
    bool hasCycle(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return false;
        }
        ListNode* slow = head;//定义慢指针
        ListNode* fast = head->next;//定义快指针
        while (slow != fast) {//相遇一直走
            if (fast == nullptr || fast->next == nullptr) {//如果无环，fast会走完链表，为空，返货false
                return false;
            }
            slow = slow->next;//慢指针一次走1步
            fast = fast->next->next;//快指针一次走2步
        }
        return true;
    }
};

时间上遍历一遍链表，所以时间复杂度是O(n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。

小结

快慢指针在解决链表的某些问题的时候，有着很好的效果。可以把题目抽象成生活案例，想想如何解决，一般就能找出解法了。

灵活运用

例题一： 链表中倒数第k个节点

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有6个节点，从头节点开始，它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。

示例 ：

给定一个链表: 1->2->3->4->5, 和 k = 2.

返回链表 4->5.

朴素地做法：

1. 用一个指针遍历一遍链表，求出链表长度：n。
2. 用一个指针从链表头开始往后走n - k 步，即可找到链表倒数第 k个节点。

//cpp
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        if(!head) return NULL;
        int len = 1;//记录链表长度.
        ListNode *p = head;
        while(p->next)
        {
            len++;
            p = p->next;
        }
        p = head;
        while(len - k)
        {
            p = p->next;
            len --;
        }
        return p;
    }
};

时间上遍历两遍链表，所以时间复杂度是O(2n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。

双指针法：

前指针 f( former首字母)、后指针l(latter首字母) ，双指针都指向头节点 head 。
构建双指针距离： 前指针先向前走k步，结束后，双指针f和l 间相距 k步。
双指针共同移动： 指针f和l每轮都向前走一步，直至 f走过链表尾节点时跳出。跳出后，l与尾节点距离为k-1，即 l指向倒数第 k 个节点。

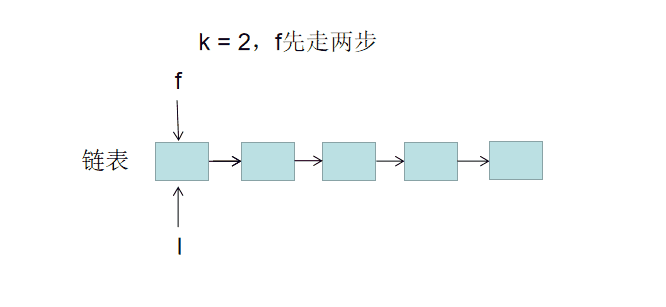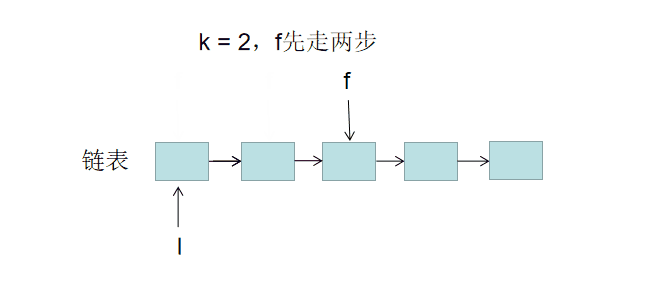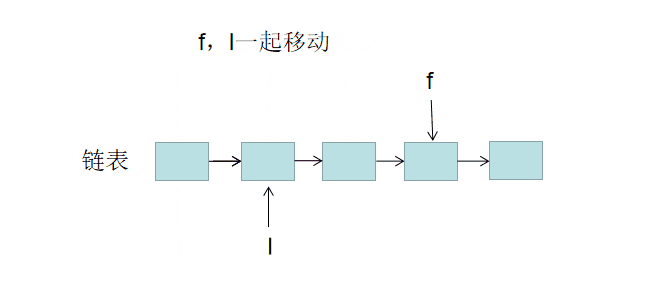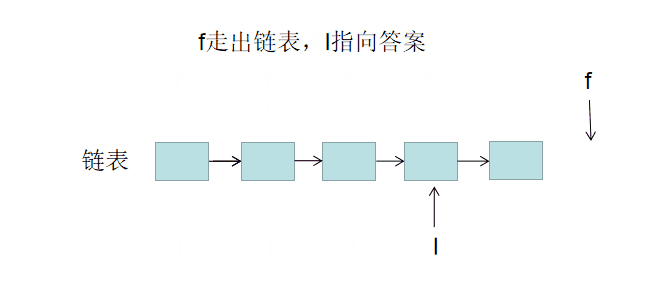
//cpp
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        if(!head || k <= 0) return NULL;    //特殊情况判定
        ListNode *f = head, *l = head;
        while(k--)  
        {
            if(!f)  return NULL;    
            f = f->next;//将p移动到第k+1个节点,默认k小于链表长度
        }
        while(f)//离开循环时f=null，为第n+1个节点,l此时在1+(n+1)-(k+1)的位置上，正好是目标节点
        {
            f = f->next;
            l = l->next;
        }
        return l;
    }
};

时间上遍历一遍链表，所以时间复杂度是O(n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。

例题二：反转字符串中的元音字母

编写一个函数，以字符串作为输入，反转该字符串中的元音字母。

示例 ：

输入："hello"
输出："holle"

双指针法：

定义指针i,j, 初始化时指针i = 0, j = s.length() - 1;
从指针i开始从左到右遍历以找到第一个元音字符，从指针j开始从右到左遍历以找到第一个元音字符;
交换指针i与指针j锁指向的元音字符即可;
指针i和指针j在遍历过程中要注意数组越界情况。

//cpp
class Solution {
    // 判断一个字符是否是元音字母
    public:
        bool isVowel(char c) {
            return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u'
                    || c == 'A' || c == 'E' || c == 'I' || c == 'O' || c == 'U' ;
        }
    public:
        string reverseVowels(string s) {
            int i = 0,j = s.size() - 1;
            while(i < j){
                if(!isVowel(s[i])){//让i指向元音
                    i++;
                    continue;
                }
                if(!isVowel(s[j])){//让j指向元音
                    j--;
                    continue;
                }
                swap(s[i++],s[j--]);//交换
            }
            return s;
        }
};

时间上遍历一遍链表，所以时间复杂度是O(n)；没有开辟与链表相关的空间，所以空间复杂度是O(1)。