https://blog.csdn.net/winter2121/article/details/72848482

一、定义

给定由n个整数（可能为负）组成的序列a1、a2、a3…,an,以及一个正整数m，要求确定序列的m个不相交子段，使这m个子段的总和最大！

特别注意：
有些题目可能不存在负数答案，给出的序列全是负数，那么不管m是多少，答案是0。此时选择的子段是0个，不足m个，但符合题意。。。
也可能有些题目要求，必须选够m个子段。
区别在dp数组的初始化。前者要求dp初始为0，后者要求第0行为0，其余为负无穷

二、解题思路：
动态规划，借助矩阵可以直观的看到计算过程。
定义二维数组dp,dp[i][j]，表示前j项所构成i子段的最大和，且必须包含第j项，即以第j项结尾。
然后是一个递推过程。
求dp[i][j],有两种情况：
1，dp[i][j]=dp[i][j-1]+a[j] 即把第j项融合到第j-1项的字段中，子段没变。
2，dp[i][j]=dp[i-1][t]+a[j] (i-1<=t<j)，把第j项作为单独的一个子段，然后找下一个i-1子段时，最大的和，然后加上a[j]。
然后比较上面两种情况，取大的。
下面看图，红色数字为输入的序列：

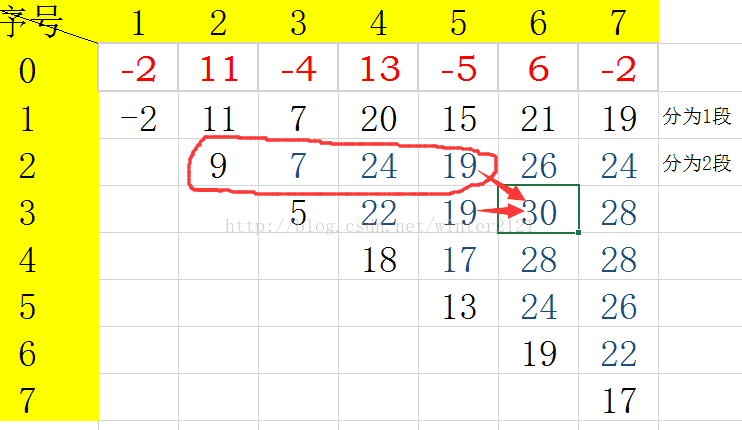
如图，要求dp[3][6]，只需要比较它左边的那个数和上面那一行圈起来的之中最大的数，在加上a[j]即为dp[3][6]的值。

优化一下：

我们可以发现对于每个dp[i][j] 的递推,我们只需要dp [ i ] [ j-1 ]  and dp[ i-1 ] [ k ] 那么我们可以利用滚动数组把空间复杂度降为 O(n);
接着我们继续看,对于每个 dp [ i ] [ j ] 的递推的时候,我们求了一遍  dp [ i ][ j ] = max{dp[ i-1 ] [ k ],dp[ i ][ j-1 ] } ( i-1<=k<= j-1 )
而在递推 dp [ i ] [ j+1 ] 的时候我们只需要比较 dp [ i ][ j ] 和 dp [ i-1 ] [ j+1 ],而不需要在循环求一次dp [ i ][ j+1 ] = max{dp[ i-1 ] [ k ],dp[ i ][ j ] }  ( i-1<=k<= j )
那么我们可以用降为 DP[ j ] 前面 j 个数字当前的最大子序列和 即是DP[j]=max{dp[ i ] [ k ]} ( i<=k<=j )
这个时候我们就可以把时间复杂度降到O(m*n);

例题：
N个整数组成的序列a[1],a[2],a[3],…,a[n]，将这N个数划分为互不相交的M个子段，并且这M个子段的和是最大的。如果M >= N个数中正数的个数，那么输出所有正数的和。
例如：-2 11 -4 13 -5 6 -2，分为2段，11 -4 13一段，6一段，和为26。

Input
第1行：2个数N和M，中间用空格分隔。N为整数的个数，M为划分为多少段。（2 <= N , M <= 5000)
第2 - N+1行：N个整数 (-10^9 <= a[i] <= 10^9)

Output
输出这个最大和

Input 示例
7 2
-2
11
-4
13
-5
6
-2

Output 示例
26

`

import java.util.*;
public class Main {
    public static void main(String[] args){
        Scanner in=new Scanner(System.in);
        int n=in.nextInt();
        int m=in.nextInt();
        int[] arr=new int[n+1];
        for(int i=1;i<=n;i++){
            arr[i]=in.nextInt();
        }
        int[] dp=new int[n+1];
        Arrays.fill(dp, 0);
        System.out.println(helper(dp,arr,n,m));
    }
    public static int helper(int[] dp,int[] arr,int n,int m){
        for(int i=1;i<=m;i++){
            int step=0;
            for(int k=1;k<=i;k++){
                step+=arr[k];
            }
            dp[n]=step;
            for(int j=i+1;j<=n;j++){
                step=Math.max(step,dp[j-1])+arr[j];
                dp[j-1]=dp[n];
                dp[n]=Math.max(step,dp[n]); //如果为最多m段的最大子序列和,那么我们可以建立一个max变量,在这里记录每个阶段dp[n],找到最大的dp[n];
            }
        }
        return dp[n];
    }
}

`

当数据量过大时上一个程序会超时：

`

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int M = sc.nextInt();
        int sum = 0;
        List<Integer> list = new ArrayList<>();
        list.add(0,0);
        int count = 0;
        for(int i= 0;i<N;i++){
            int num = sc.nextInt();
            if(count>0){
                if(num>=0){
                    count+=num;
                }else{
                    list.add(count);
                    count = num;
                }
            }else if(count<0){
                if(num>=0){
                    list.add(count);
                    count = num;
                }else{
                    count+=num;
                }
            }else{
                count+=num;
            }
        }
        if(count>0){
            list.add(count);
        }
        //System.out.println(list.size());
        if (M >= list.size()) {
            for (int i = 1; i <=N; i++) {
                if (list.get(i) > 0) {
                    sum += list.get(i);
                }
            }
            System.out.println(sum);
        } else {
            int[][] dp = new int[2][N + 1];
            Arrays.fill(dp[0], 0);
            Arrays.fill(dp[1], 0);
            int res = Integer.MIN_VALUE;
            for (int i = 1, k = 1; i <= M; i++, k ^= 1) { //k为两行之间的切换
                dp[k][i - 1] = Integer.MIN_VALUE;
                int maxPre = Integer.MIN_VALUE;//记录上一行的最大值
                for (int j = i; j < list.size(); j++) {//沿着第M行的最后一个元素，往左上方画一条线，线右上方的元素是没有必要计算的，故j的上限为i+N-M;
                    maxPre = Math.max(maxPre, dp[k ^ 1][j - 1]);//随时更新上一行的最大值
                    dp[k][j] = Math.max(dp[k][j - 1], maxPre) + list.get(j);
                    res = Math.max(res, dp[k][j]);
                }
            }
            System.out.println(res);
        }
    }
}

`