基础知识
整除
对于正整数 $n$,$m$,如果存在整数 $q$ 使得 $n = qm$,则称 $m$ 整除 $n$,记做 $m \mid n$。
称 $m$ 是 $n$ 的约数,$n$ 是 $m$ 的倍数。
最大公约数
对于正整数 $a$,$b$,若正整数 $d$ 满足 $d \mid a$ 且 $d \mid b$,则称 $d$ 是 $a$ 和 $b$ 的公约数。
$a$ 和 $b$ 最大的公约数称为 $a$,$b$ 的最大公约数,记做 $gcd(a, b)$ 或者 $(a, b)$。
$d$ 是 $a$,$b$ 的公约数等价于 $d \mid gcd(a, b)$。
互质
若正整数 $a$,$b$ 满足 $gcd(a, b) = 1$,则称 $a$ 与 $b$ 互质。
有时也记做 $a \bot b$。
取整函数
对于实数 $x$,记 $\left\lfloor x \right\rfloor$ 为不超过 $x$ 的最大整数。
$\left\lfloor x \right\rfloor$ 也是满足如下关系的唯一 函数:
$$\left\lfloor x \right\rfloor \leqslant x < \left\lfloor x \right\rfloor + 1$$
对于正整数 $n$,$1$ 到 $n$ 中 $d$ 的倍数有 $\left\lfloor \frac{n}{d} \right\rfloor$ 个。
我们时常要考虑形如 $\left\lfloor \frac{n}{d} \right\rfloor$ 的数。
为行文方便,后文可能会将这些数称为特殊点。(比如杜教筛)
性质
-
对于任意的 $x$ 与正整数 $a$,$b$,我们均有:
$$\left\lfloor \frac{\lfloor \frac{x}{a} \rfloor}{b} \right\rfloor = \lfloor \frac{x}{ab} \rfloor$$ -
对于整数 $n$,考虑当 $1 \leqslant d \leqslant n$ 时,$\lfloor \frac{n}{d} \rfloor$ 的不同的取值个数。
若 $d \leqslant \sqrt{n}$,则能得到的 $\lfloor \frac{n}{d} \rfloor$ 只有不超过 $\sqrt{n}$ 种。
若 $d > \sqrt{n}$,则 $\lfloor \frac{n}{d} \rfloor \leqslant \frac{n}{d} \leqslant \sqrt{n}$,又因为 $\lfloor \frac{n}{d} \rfloor$ 是正整数,故此时可能的取值也不超过 $\sqrt{n}$ 种。
综上,$\lfloor \frac{n}{d} \rfloor$ 可能的取值不超过 $2\sqrt{n}$ 种。(又称数论分块)
例题1
求
$$\sum_{d=1}^n \lfloor\frac{n}{d}\rfloor$$
$n \leqslant 10^{12}$。
对于 $\lfloor \frac{n}{d} \rfloor$ 的每个取值,对应的 $d$ 的范围是一个区间。枚举 $\lfloor\frac{n}{d}\rfloor$ 的取值即可。
附代码:
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using ll = long long;
int main() {
ll n;
cin >> n;
ll ans = 0;
for (ll i = 1; i <= n; ++i) { // i为d的左端点,j为d的右端点
ll t = n / i, j = n / t;
ans += (j - i + 1) * t;
i = j;
}
cout << ans << '\n';
return 0;
}
调和数
调和数定义为 $H_n = \sum_{k=1}^n \frac{1}{k}$。
关于调和数有如下结论:
$$H_n = \ln n + \gamma + o(1)$$
这可以推出一个常见的时间复杂度:
$$\sum_{d=1}^n \lfloor \frac{n}{d} \rfloor = \Theta (n\log n)$$
素数
如果一个数 $p$ 的约数只有 $1$ 和 $p$ 自身,则称 $p$ 为素数。
算数基本定理
任意一个正整数 $n$ 都可以表示成素数的乘积的形式:
$$n = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_s^{\alpha_s}$$
其中$p_1, \cdots, p_s$ 是不同素数。且不计次序的情况下,这一表达是唯一的。
求素数
求不超过 $n$ 的所有素数可以用 $O(n)$ 的 $Euler$ 筛法。
其思想是枚举每个数的最小素因子。
素数计数函数
令素数计数函数 $\pi(n)$ 表示不超过 $n$ 的素数个数。我们有如下的素数定理:
$$\pi(n) \sim \frac{n}{\ln n}$$
推论:
- $n$ 附近的素数密度近似是 $\frac{1}{\ln n}$
- 第 $n$ 个素数 $p_n \sim n\log n$
素数计数
显然可以利用 $Euler$ 筛算出 $n$ 以内的所有素数,进而得到 $\pi(n)$。
存在更快的做法。
用一种类似积性函数求和的筛法可以达到 $O(\frac{n^{\frac{3}{4}}}{\log n})$ 的复杂度。
先进的做法似乎可以达到 $O(\frac{n^{\frac{2}{3}}}{\log n})$。
数论函数
定义域为正整数、值域是复数的子集的函数称为数论函数。
但竞赛中研究的数论函数的值一般也是整数。
积性函数
- 设 $f$ 是数论函数,若对任意互质的正整数 $a, b$,都有 $f(ab) = f(a)f(b)$,则称 $f$ 是积性函数。
-
若对任意的正整数 $a, b$,都有 $f(ab) = f(a)f(b)$,则称 $f$ 是完全积性的。
-
若 $f$ 是积性函数,且 $n = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_s^{\alpha_s}$ 是 $n$ 的标准分解, 则有
$$f(n) = f(p_1^{\alpha_1})f(p_2^{\alpha_2}) \cdots f(p_s^{\alpha_s})$$
因此研究积性函数 $f$ 可以转化为研究 $f(p^\alpha)$,即 $f$ 在素数和素数的幂上的取值。
积性函数求值
- 设 $f$ 是积性函数,为求 $f(n)$ 可以先对 $n$ 分解素因子,然后计算所有的 $f(p^{\alpha})$ 乘起来。
- 如果要对 $1$ 到 $n$ 之间的所有数求出 $f$,注意到 $Euler$ 筛法的过程中可以求出每个数的最小素因子和最小素因子的幂次,利用此就能在线性时间内计算出所需的 $f$ 的值。
单位函数
单位函数 $\varepsilon(n)$ 定义为:
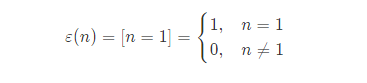
其中 [condition] 表示 condition 为真时取值为 $1$,否则为 $0$ 的函数。
单位函数是完全积性函数。
除数函数
除数函数 $\sigma_k(n)$ 用来表示 $n$ 的因子的 $k$ 次方之和:
$$\sigma_k\left( n \right) = \sum\limits_{\left. d \right|n} {{d^k}} $$
约数个数 $\sigma_0 (n)$ 常记为 $d(n)$,约数和 $\sigma_1 (n)$ 常记为 $\sigma(n)$。
除数函数都是积性涵数。
欧拉函数
$Euler$ 函数 $\varphi(n)$ 表示不超过 $n$ 且与 $n$ 互素的正整数的个数。
由 $n$ 的标准分解并结合容斥原理,我们可以得到 $n$ 的显式表达式 :
$$ \varphi \left( n \right) = n \cdot \prod\limits_{i = 1}^n {\left( {1 - \frac{1}{{{p_i}}}} \right)} $$
其中 $ n = p_1^{{\alpha _1}}p_2^{{\alpha _2}} \cdots p_s^{{\alpha _s}} $ 是 $n$ 的标准分解。
由此易见 $Euler$ 函数是积性函数。
Euler 函数的性质
对于任意 $n$,$Euler$ 函数有如下性质:
$$ n = \sum\limits_{\left. d \right|n} {\varphi \left( d \right)} $$
要证明这个等式,我们将 $1$ 到 $n$ 中的所有整数按与 $n$ 的最大公约数分类。
若 $gcd(n, i) = d$,那么 $gcd(\frac{n}{d}, \frac{i}{d}) = 1$。而又 $\frac{i}{d}$ 是不超过 $\frac{n}{d}$ 的整数,故这样的 $i$ 有 $\varphi(\frac{n}{d})$ 个。
考虑所有 $d \mid n$,我们也就考虑到了所有 $1$ 到 $n$ 之间的 $n$ 个整数,因此有
$$ n=\sum\limits_{\left. d \right|n} {\varphi \left( {\frac{n}{d}} \right)} = \sum\limits_{\left. d \right|n} {\varphi \left( d \right)} $$
Dirichlet 卷积
设 $f, g$ 是数论函数,考虑数论函数 $h$ 满足
$$h\left( n \right) = \sum\limits_{\left. d \right|n} {f\left( d \right)g\left( {\frac{n}{d}} \right)} $$
则称 $h$ 为 $f$ 和 $g$ 的 $Dirichlet$ 卷积,记做 $h = f * g$。
Dirichlet 卷积的性质
- 单位函数 $\varepsilon$ 是 $Dirichlet$ 卷积的单位元,即对于任意函数 $f$,有 $\varepsilon * f = f * \varepsilon = f$。
$Dirichlet$ 卷积满足交换律和结合律。 - 如果 $f, g$ 都是积性函数,那么 $f * g$ 也是积性函数。
许多关系都可以用狄利克雷卷积来表示。
下面用 $1$ 来表示取值为 $1$ 的常函数,定义幂函数 $I{d_k}\left( n \right) = {n^k},Id = I{d_1}$。
除数函数的定义可以写为:${\sigma _k} = 1*I{d_k}$
欧拉函数的性质可以写为:$Id = \varphi *1$
计算Dirichlet卷积
设 $f, g$ 是数论函数,计算 $f$ 和 $g$ 的 $Dirichlet$ 卷积在 $n$ 处的值需要枚举 $n$ 的所有约数。
如果要计算 $f$ 和 $g$ 的 $Dirichlet$ 卷积的前 $n$ 项,可以枚举 $1$ 到 $n$ 中每个数的倍数,根据调和数的相关结论,这样做的复杂度是 $O(n\log n)$。
Mobius 函数
$\color{blue}{Mobius}$ 函数 $\color{red}{\mu(n)}$ 定义为:
$$
\mu(n) = \begin{cases}
1, & n = 1; \\\
(-1)^s, & n = p_1p_2 \cdots p_s; \\\
0, & otherwise.
\end{cases}
$$
其中 $p_1, p_2, \cdots, p_s$ 是不同素数.
可以看出,$\mu(n)$ 恰在 $n$ 无平方因子时非零.
易见 $\color{red}{\mu}$ 是积性函数.
Mobius 函数的性质
$\color{blue}{Mobius}$ 函数具有如下最重要的性质:
$$\displaystyle \sum_{d \mid n} \mu(d) = \varepsilon(n)$$
使用 $\color{blue}{Dirichlet}$ 卷积来表示,即
$$\mu * 1 = \varepsilon$$
证明:
$n = 1$ 时显然成立。
若 $n > 1$,设 $n$ 有 $s$ 个不同的素因子,由于 $\mu(d) \neq 0$ 当且仅当 $d$ 无平方因子,故 $d$ 中每个素因子的指数只能为 $0$ 或 $1$。故有
$$ \displaystyle \sum_{d \mid n} \mu(d) = \sum_{k = 0}^s (-1)^k \binom{s}{k} = (1 - 1)^s = 0 $$
这就证明了 结论。
Mobius 变换
设 $f$ 是数论函数,定义函数 $g$ 满足
$$ g(n) = \sum_{d \mid n} f(d) \tag{1} $$
则称 $g$ 是 $f$ 的 $\color{blue}{Mobius}$ 变换,$f$ 是 $g$ 的 $\color{blue}{Mobius}$ 逆变换。
用 $\color{purple}{Dirichlet}$ 卷积表示即为 $g = f * 1$。
Mobius 反演
$\color{blue}{Mobius}$ 反演定理指出,$(1)$ 的充要条件为:
$$ f(n) = \sum_{d \mid n} g(n) \mu(\frac{n}{d}) \tag{2} $$
证明可以使用 $\color{purple}{\rm Dirichlet}$ 卷积:
$$ g = f * 1 \Leftrightarrow f = f * \varepsilon = f * 1 * \mu = g * \mu $$
应用
利用 $\color{purple}{\rm Dirichlet}$ 卷积可以解决一系列求和问题。常见做法是使用一个 $\color{purple}{\rm Dirichlet}$ 卷积替换求和式中的一部分,然后调换求和顺序,最终降低时间复杂度。
经常利用的卷积有 $\mu * 1 = \varepsilon$ 和 $Id = \varphi * 1$。
无平方因子数
求 $n$ 以内无平方因子数的个数。亦即,求
$$ \sum_{k = 1}^n \mu^2(k) $$
我们考虑一个素数 $p$,那么 $p^2$ 的倍数都有平方因子,个数是 $\lfloor \frac{n}{p^2} \rfloor$,应该从答案中去掉。
但是这样多去掉了一些数。比如对于不同的素数 $p_1, p_2, p_1^2p_2^2$ 的倍数就被去掉了两次,个数是 $\lfloor \frac{n}{p_1^2 p_2^2} \rfloor$,应该加回来。
显然这是容斥原理。
如果 $d$ 是 $s$ 个不同素数的乘积,那么其对答案的贡献是 $(-1)^s \lfloor \frac{n}{d^2} \rfloor$。
如果 $d$ 不是不同素数的乘积,即 $d$ 有平方因子,那么 $d$ 对答案没有贡献。
容斥的系数恰好是 $\color{blue}{\rm Mobius}$ 函数。
因此答案就是
$$ \sum_{k=1}^n \mu^2(k) = \sum_{d = 1}^{\sqrt{n}} \mu(d) \lfloor \frac{n}{d^2} \rfloor $$
事实上,$\color{blue}{\rm Mobius}$ 反演本身就可以看成是对整除关系的容斥。
莫比乌斯反演是在有序偏序集上的容斥,容斥是莫比乌斯反演在有序偏序集上的实例。
数论函数求和
杜教筛
有一种利用 $\color{purple}{\rm Dirichlet}$ 卷积来构造递推式,从而对一些数论函数进行求和的方法。
民间称呼$\color{green}{杜教筛}$。
我们用两个例子来了解一下这个方法。
Euler 函数的前缀和
令
$$ \phi(n) = \sum_{i = 1}^n \varphi(i) $$
我们考虑如何高速的求出 $\phi(n)$。
考虑到 $\rm Id = \varphi * 1$,我们有:
$$ \begin{aligned} \frac{1}{2}n(n + 1) &= \sum_{k = 1}^n k = \sum_{k = 1}^n \sum_{d \mid k} \varphi(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{1 \leqslant k \leqslant n \atop d \mid k} \varphi(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor} \varphi(k) = \sum_{d = 1}^n \phi(\lfloor \frac{n}{d} \rfloor) \end{aligned} $$
我们可以得到:
$$ \phi(n) = \frac{1}{2}n(n + 1) - \sum_{d = 2}^n \phi(\lfloor \frac{n}{d} \rfloor) $$
因此,如果对于 $2 \leqslant d \leqslant n$ 已经计算出了 $\phi(\lfloor \frac{n}{d} \rfloor)$,即特殊点处的函数值,由于特殊点不超过 $2\sqrt{n}$ 个,利用之前见过的分段的方法,我们可以在 $O(\sqrt{n})$ 的时间内计算出 $\phi(n)$。
而计算 $\phi(\lfloor \frac{n}{d} \rfloor)$ 是子问题,可以递归解决。
递归过程中会不会需要计算更多的函数值?
由特殊点的性质,可以发现所有要计算的就是所有特殊点处的函数值。
使用记忆化搜索,这样每个函数值只会被计算一遍。
时间复杂度分析
算法的时间复杂度就是计算所有特殊点处的函数值的时间复杂度。
回忆特殊点的结构,时间复杂度 $T(n)$ 可以估计为
$$ T(n) = \sum_{i = 1}^{\sqrt{n}}O(\sqrt{i}) + \sum_{i = 1}^{\sqrt{n}}O\left(\sqrt{\lfloor \frac{n}{i} \rfloor}\right) $$
显然式中第一项渐进意义上小于第二项。
而对于式中第二项我们可以利用积分估计:
$$ \sum_{i = 1}^{\sqrt{n}}O\left(\sqrt{\lfloor \frac{n}{i} \rfloor}\right) = O\left(\int_1^{\sqrt{n}} \sqrt{\frac{n}{x}}{\rm d} x\right) = O(n^{\frac{1}{2}} \cdot n^{\frac{1}{4}}) = O(n^{\frac{3}{4}}) $$
于是算法的时间复杂度为 $O(n^{\frac{3}{4}})$。
注意到我们还可以使用 $\rm Euler$ 筛求出 $\varphi$ 的值,进而求出前缀和。
假设我们使用 $\rm Euler$ 筛预先求出了 $\varphi$ 的前 $S$ 项,那么递归部分的时间复杂度变为:
$$ \sum_{i = 1}^{\frac{n}{S}} O\left(\left\lfloor \frac{n}{i} \right\rfloor\right) = O\left(\int_1^{\frac{n}{S}} \sqrt{\frac{n}{x}} {\rm d} x \right) = O\left(n^{\frac{1}{2}} \cdot \sqrt{\frac{n}{S}}\right) = O\left(\frac{n}{S^{\frac{1}{2}}}\right) $$
结合 $\rm Euler$ 筛的时间复杂度 $O(S)$,总的时间复杂度为 $O(S + \frac{n}{S^{\frac{1}{2}}})$。
如果取 $S = n^{\frac{2}{3}}$,那么总的时间复杂度为 $O(n^{\frac{2}{3}})$。
#include <cstdio>
typedef long long ll;
const ll XN = 1000000000, XR = 1000031;
bool ip[XR];
int p[XR / 10], c = 0;
ll phi[XR], sphi0[XR];
ll sphi[XN / XR + 100];
ll n = 1000000000;
// 预处理2/3
void sieve() {
ip[0] = ip[1] = 1;
phi[1] = 1;
for (int i = 2; i < XR; ++i) {
if (!ip[i]) p[c++] = i, phi[i] = i - 1;
for (int j = 0; j < c and i * p[j] < XR; ++j) {
ip[i * p[j]] = 1;
if (i % p[j]) phi[i * p[j]] = phi[i] * (p[j] - 1);
else {
phi[i * p[j]] = phi[i] * p[j];
break;
}
}
}
for (int i = 1; i < XR; ++i) sphi0[i] = sphi0[i - 1] + phi[i];
}
ll calc(ll k) {
if (k < XR) return sphi0[k];
else {
auto &z = sphi[n / k];
if (!z) {
z = k * (k + 1) / 2;
for (ll i = 2; i <= k; ++i) {
ll t = k / i, j = k / t;
z -= (j - i + 1) * calc(t);
i = j;
}
}
return z;
}
}
int main() {
sieve();
printf("%lld\n", calc(n));
return 0;
}
Mobius 函数的前缀和
令
$$M\left( n \right) = \sum\limits_{k = 1}^n {\mu \left( k \right)} $$
计算的过程与 $\varphi$ 是类似的。不过这次需要使用 $\mu * 1 = \varepsilon$。
$$ \begin{aligned} 1 &= \sum_{k = 1}^n \varepsilon(k) = \sum_{k = 1}^n \sum_{d \mid k} \mu(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{1 \leqslant k \leqslant n \atop d \mid k} \mu(\frac{k}{d}) = \sum_{d = 1}^n \sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor} \mu(k) = \sum_{d = 1}^n M(\lfloor \frac{n}{d} \rfloor) \end{aligned} $$
于是可以得到
$$ M(n) = 1 - \sum_{d = 2}^n M\left(\left\lfloor\frac{n}{d}\right\rfloor\right) $$
用同样的方法递推即可。
一般化
在求 $\varphi$ 和 $\mu$ 的前缀和的过程中,我们都利用了一个 $\color{purple}{\rm Dirichlet}$ 卷积。
这就让我们考虑数论函数 $f, g$ 的前缀和与它们的 $\color{purple}{\rm Dirichlet}$ 卷积 $f*g$ 的前缀和之间的关系。
用 $F$ 表示 $f$ 的前缀和,我们有
$$ \begin{aligned} \sum_{k = 1}^n (f * g)(k) &= \sum_{k = 1}^n\sum_{d \mid k} f(\frac{k}{d})g(d) \\\ &= \sum_{d = 1}^n\sum_{1 \leqslant k \leqslant n \atop d \mid k} g(d)f(\frac{k}{d}) = \sum_{d = 1}^n g(d)\sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor}f(k) \\\ &= \sum_{d = 1}^n g(d)F(\lfloor \frac{n}{d} \rfloor) \end{aligned} $$
在上两例中,$f*g$ 和 $g$ 的前缀和都可以 $O(1)$ 得出,因此 $f$ 可以用杜教筛计算。
其实并不需要如此强的性质。
可以看到,在杜教筛的过程中,我们实际上求出了所有特殊点处的前缀和。
注意到 $g$ 的前缀和是对使得 $\lfloor \frac{n}{d} \rfloor$ 相同 $d$ 分段的时候用到的,因此只需要用到 $g$ 在段落端点处的前缀和。
可以发现,段落的端点恰好是所有的特殊点。
因此,$f, g$ 以及 $f*g$ 这三个函数中,只要有两个可以用不弱于杜教筛的方法求值,就可以杜教筛第三个。
约数个数求和
求
$$\sum_{k = 1}^n \sigma_0 (k)$$
杜教筛?
$$\sum_{k = 1}^n \sigma_0 (k) = \sum_{k = 1}^n \sum_{d \mid k} 1 = \sum_{d = 1}^n \lfloor \frac{n}{d} \rfloor$$

