曾经，有一个人叫暴力枚举。有一天，他遇见了区间最值。然后，他死了。

曾经，有一个人叫暴力查询。有一天，他遇见了区间信息统计。然后，他也死了。

为了减少伤亡，于是，ST 算法和线段树横空出世！

ST 算法

ST 算法，是倍增思想经典的体现，专门用来求解 RMQ (区间最值问题)
ST 算法在经过 O(NlogN) 时间的预处理后，能以 O(1) 的时间复杂度在线回答区间最值问题

而 ST 算法的主要思想其实就一条：用两个 2 的整数次幂长度的区间，刚好覆盖所求区间。

具体实现：

1.预处理出以每个点为开始，长度为 2 ^ j ,j ∈ [0 , log(n) / log(2) + 1] 的区间最值

2.查询时，对于给定区间 [l , r] 和区间长度 len ，

我们用以 l 开头，长度刚好大于 len/2且为 2 的整数次幂的区间

用以 r 结尾，长度刚好大于 len/2且为 2 的整数次幂的区间，

两者一定刚好覆盖整个区间 [l , r] ，所以所求为两区间预处理答案中的最值。

代码：

const int N=100000+10;

int n,q,k;
int a[N];
int maxn[N][20],minn[N][20];

//maxn[i][j]表示的是以 i 为起点，长度为 2 ^ j 区间内的最大值   <==>   [i,i + 2 ^ j -1]
//minn 类同

void st_prework()
{
    for(int i=1;i<=n;i++) maxn[i][0]=a[i],minn[i][0]=a[i];
    int k=log(n)/log(2)+1;
    for(int j=1;j<k;j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            maxn[i][j]=max(maxn[i][j-1],maxn[i+(1<<(j-1))][j-1]);
    for(int j=1;j<k;j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
}

int ST_query(int l,int r)
{
    int k=log(r-l+1)/log(2);
    //2 ^ k >= len / 2,所以 max(l , r)=max(max(l , l + 2 ^ k - 1),max(r - 2 ^ k + 1 , r)) 最小类同 
    //最大最小都是单调的，只要区间覆盖即可 
    //return max(maxn[l][k],maxn[r-(l<<k)+1][k])-min(minn[l][k],minn[r-(l<<k)+1][k]);
    return max(maxn[l][k],maxn[r-(1<<k)+1][k])-min(minn[l][k],minn[r-(1<<k)+1][k]);
}

另一可求解区间的数据结构是线段树

线段树

什么是线段树呢？

如图：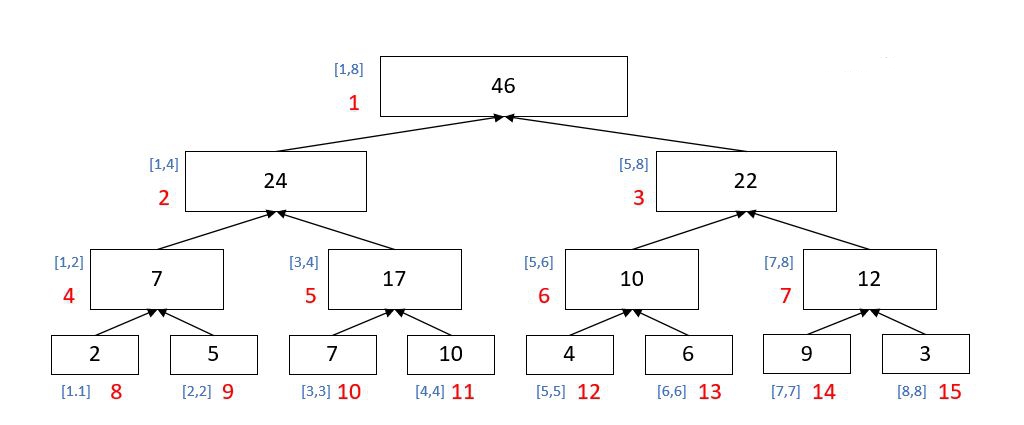

线段树就是一棵记录了区间信息的二叉树。

它以整个区间为根节点，不断二分并把二分产生的新区间作为新节点加入到树中

这样，无论是怎样的区间 [l , r] ，我们都可以用几个树上的点把它表示出来，即将几段相邻的区间合并。

这样，我们可以很方便地记录并修改区间信息。

相对于 ST 算法，线段树显然更加通用，如最值问题，显然也可以用线段树求解。

关于线段树的实现:

我们以 AcWing 243 为例

题面：

给定一个长度为N的数列A，以及M条指令，每条指令可能是以下两种之一：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问 数列中第 l~r 个数的和。

对于每个询问，输出一个整数表示答案。

分析：

这就是区间信息的统计与修改，是线段树的模板。

1.建树

线段树是一棵二叉树，所以很明显父节点等于二子节点权值的和。

那么只要不断递归左右子节点，再在回溯时跟新就行了。

代码实现：

const int N=100000+10;

int a[N];
struct TREE
{
    int l,r;
    //区间范围
    ll dat,tag;
    //dat 是记录的信息，tag 是懒标记
}t[N*4];

void build(int rt,int l,int r)
{
    t[rt].l=l,t[rt].r=r;

    if(l==r)
    {
        t[rt].dat=a[l];
        //单点区间已经不能再分
        return ;
    }

    int mid=(l+r)>>1;

    build(rt*2,l,mid);
    build(rt*2+1,mid+1,r);
    //分别递归左子树和右子树

    t[rt].dat=t[rt*2].dat+t[rt*2+1].dat;
    //回溯时跟新
}

//build(1,1,n);

2.关于懒标记

怎么说呢，懒标记是真的懒

在进行区间修改时，对区间内的每一个小区间也要递归修改。

这是非常耗时的。真的懒

于是我们决定能不修改小区间就不修改小区间(因为对于每个大区间，小区间都继承了它的修改信息)

并把修改信息累计在大区间，等到需要回答问题时，一起递归累计。

是不是非常方便？是真的懒

所以，所谓懒标记，就是了累计的修改信息，时刻准备传递给下一层区间。

代码实现：

//
void spread(int rt)
{
    if(t[rt].tag)
    {
        int ls=rt*2,rs=rt*2+1,lazy=t[rt].tag;
        //  左子树  右子树

        t[ls].dat+=lazy*(t[ls].r-t[ls].l+1),t[ls].tag+=lazy;
        t[rs].dat+=lazy*(t[rs].r-t[rs].l+1),t[rs].tag+=lazy;
        //修改小区间信息并更新懒标记

        t[rt].tag=0;
        //大区间的信息已经传给下一层了
    }
}

3.关于区间修改

之前我们已经说了，任何区间都能由几个树上的节点，即几段连续的区间合并成

那么我们需要做的，就是找到那几个点，修改信息并更新懒标记。(之后询问时再更新小区间)

代码实现

void change(int rt,int l,int r,int val)
{
    if(l<=t[rt].l&&r>=t[rt].r)
    {
        t[rt].dat+=(ll)val*(t[rt].r-t[rt].l+1);
        t[rt].tag+=val;
        //如果一个节点所表示的区间被修改区间覆盖，那它就是连续区间的一段
        //它所包涵的小区间都不用修改，只要修改懒标记就行了
        return ;
        //因为不用修改，我们直接返回
    }

    spread(rt);
    //为了保证懒标记只在最新的区间上

    int mid=(t[rt].l+t[rt].r)>>1;

    if(l<=mid) change(rt*2,l,r,val);
    if(r>=mid+1) change(rt*2+1,l,r,val);

    t[rt].dat=t[rt*2].dat+t[rt*2+1].dat;
    //递归回溯就不用我说了吧。。
}

4.关于查询

查询与修改本质上是一样的，也是找一段连续的区间然后加起来，不要忘记懒标记的更新就行了

代码实现

ll query(int rt,int l,int r)
{
    if(l<=t[rt].l&&r>=t[rt].r) return t[rt].dat;
    //如果覆盖的话，直接返回这段区间

    spread(rt);

    int mid=(t[rt].l+t[rt].r)>>1;
    long long ans=0;

    if(l<=mid) ans+=query(rt*2,l,r);
    if(r>=mid+1) ans+=query(rt*2+1,l,r);

    return ans;
    //感觉该说的都说了~~我被懒标记感染了。。~~
}

后记

其实 ST 和线段树很多人都会，而且有很多人写，但是前几天知道某些人不会，啧啧，所以我写一写。。