更好的阅读体验
一篇今天刚出炉的还挂在arxiv上的很有意思的基于对抗样本攻击的神经网络架构搜索(NAS)
这里主要介绍它的思路
首先总结文章的主要思想:通过搜索一个解释网络A“更好的解释目标任务”,解释的准则是通过对抗攻击样本学一个像素位置权重$\delta x$对样本加权后扔给听众网络$f$,搜索的联合目标是让听众网络$f$和解释器网络$A$的验证损失最小
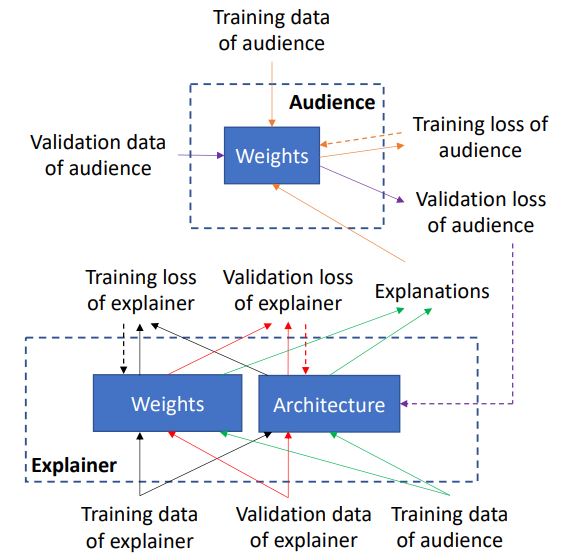
在框架中,有一个解释器模型和一个听众模型,它们都学习执行相同的目标任务。框架的主要目标是帮助解释器很好地学习目标任务。 实现此目标的方法是让解释器对目标任务中的预测结果进行有意义的解释。
$learning{~}by{~}self-explanation (LeaSE)$的直觉是:为了正确解释预测结果,模型需要学习很好地理解目标任务。 解释者具有可学习的网络结构$A$和一组可学习的网络权重$E$。听众具有预定义的神经网络结构(由人类专家设计)和一组可学习的网络权重$W$。学习分为四个阶段。
- 在第一阶段,解释器在固定的架构下,在其训练数据集$D(tr)_e$上训练其网络权重$E$
$$ E^{*}(A)=\min_{E} L\left(E, A, D_{e}^{(\mathrm{tr})}\right) $$
架构$A$用于定义训练损失。 但是,此阶段尚未更新$A$。如果通过最小化训练损失来学习$A$,则在$A$很大且很复杂的情况下,如果它可以完全拟合训练数据,而在看不见的数据上推广得很差,那么将产生一个简单的解决方案。 注意,最佳训练权重$E^{∗}(A)$是$A$的函数,因为$E^{∗}(A)$是$L(E,A,D(tr)_{e})$和$L(E,A,D(tr)_{e}$的函数是$A$的函数。
- 在第二阶段,解释器使用训练后的模型$E^{*}(A)$对输入的听众训练示例$D(tr)_{a}$进行预测,并解释预测结果。
具体来说,给定输入数据示例$x$(在不失一般性的前提下,我们假设它是一幅图像)和预测标签$y$,解释者的目的是找出$x$中大部分与$y$相关的图像子集块$P$,并使用$P$作为$y$的解释。 利用对抗性攻击方法来实现这一目标。
$$ \Delta^{∗}\left(E^{∗}(A)\right)=\max_{\Delta} \sum_{i=1}^{N} \ell\left(f\left(x_{i}+\delta_{i} ; E^{∗}(A)\right), f\left(x_{i} ; E^{∗}(A)\right)\right) $$
其中$∆ = {δ_{i}} N_{i} = 1$且$δ_{i}$是添加到图像$x_{i}$的摄动。 $f(x_{i} +δ_{i}; E^{∗}(A))$和$f(x_{i}; E^{∗}(A))$是解释者网络$f(·; E^{∗}(A))$对$x_{i} +δ_{i}$和$x_{i}$的预测结果。 不失一般性,我们假设任务是图像分类(具有$K$个类)。 则$f(x_{i} +δ_{i}; E ^{∗}(A))$和$f(x_{i}; E^{∗}(A))$均为$K$维向量,其中包含关于$K$类的预测概率。 $l(·,·)$是$l(a,b)= \sum_{K}^{k = 1} b_{i} log (a_{i})$的交叉熵损失
在这个优化问题中,解释器目的是找出每个图像的扰动,以使扰动图像上的预测结果与原始图像上的预测结果不相同。 所学习的最佳扰动作为解释,值较大的扰动表明相应的像素在决策中更为重要。
即主要思路:给图像加入随机扰动,找到导致损失函数最大的那个扰动,则这个最大的扰动中各个位置的扰动大小就对应了各个位置对任务的影响
- 在第三阶段,给定解释器的解释$Δ^{∗}(E ^{∗}(A))$,听众可以利用它们来学习目标任务。 由于扰动指示输入像素的重要性,因此听众使用它们来重新对各个像素赋权:$x\bigodot δ$,其中$\bigodot $表示逐元素乘法。 更重要的像素将获得更多权重。 然后,听众网络在这些加权后的图像上训练其网络权重:
$$ W^{*}\left(\Delta^{∗}\left(E^{∗}(A)\right)\right)=\min_{W} \sum_{i=1}^{N} \ell\left(f\left(\delta_{i}^{∗}\left(E^{∗}(A)\right) \odot x_{i} ; W\right), t_{i}\right) $$
其中$f(δ_{i}^{∗} (E^{∗}(A))x_{i}; W)$是听众网络$f(·; W)$在加权图像$δ_{i}^{∗}(E ^{∗}(A))x_{i}$上的预测结果,$t_{i}$是 类标签。 注意$W^{∗}(∆^{∗}(E^{∗}(A)))$是$∆^{∗}(E ^{∗}(A))$的函数,因为$W^{∗}(∆^{∗}(E^{∗}(A)))$是$Eq3$中目标的函数 ,并且目标是$∆^{∗}(E ^{∗}(A))$的函数。
- 在第四阶段,解释器在其验证集$D_{e}^{val}$上验证其网络权重$E^{∗}(A)$,听众在其验证集$D_{a}^{val}$上验证其网络权重$W^{∗}(∆^{∗}(E^{∗}(A)))$一个。解释器A通过最小化自己的验证损失和听众的验证损失来优化其架构A
即搜一个能让A的验证损失和听众网络的验证损失最小的A
$$ \min _{A} L\left(E^{∗}(A), D_{e}^{(\mathrm{val})}\right)+\gamma L\left(W^{∗}\left(\Delta^{∗}\left(E^{∗}(A)\right)\right), D_{a}^{(\mathrm{val})}\right) $$
总结
-
在第一阶段学习的当前A的参数:$E^{∗}(A)$用于定义第二阶段的目标函数;
-
第二阶段固定A通过对抗样本攻击学习的位置的重要性权重:$∆^{∗}(E^{∗}(A))$用于定义第三阶段的目标函数;
-
在第一阶段的解释器网络参数$E^{∗}(A)$和第三阶段学习的观众网络参数$W^{∗}(∆^{∗}(E^{∗}(A)))$用于定义第四阶段的目标;
-
第四阶段中更新$A$后依次更改了第一阶段中的目标函数,随后对$E^{∗}(A),∆^{∗}(E^{∗}(A))$和$W^{∗}(∆ ^{∗}(E^{∗}(A)))$进行更改。

