Kmp算法是什么？
判定字符串A是否是字符串B的字串，并求出字符串A在字符串B中各次出现的位置
这个算法有什么用？
常用的百度搜索引擎，关键字搜索，是不是得找出用户搜索的关键字在各个网页中的出现位置啊，当然了，还有更重要的用途，，算法考试是吧，

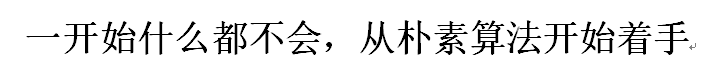
从A的第一个下标开始，发现前4个m都匹配上了，就是B的第5个字符调皮，搞得这一次没有匹配成功，

然后从第二个下标开始继续比较，
欸，重点来了，，我们人眼可见的从下标2开始前四个字符已经匹配成功了，而机器仍然要从最左边的m开始进行4次比较，
或者说，不应该责怪计算机没有长眼睛，，他应该改进的是前四个字符在第一次匹配过程中已经比较过了，而它第二次还要再次比较这四个字符，


留下什么？ 或者换一种问法，后续的比较需要什么？
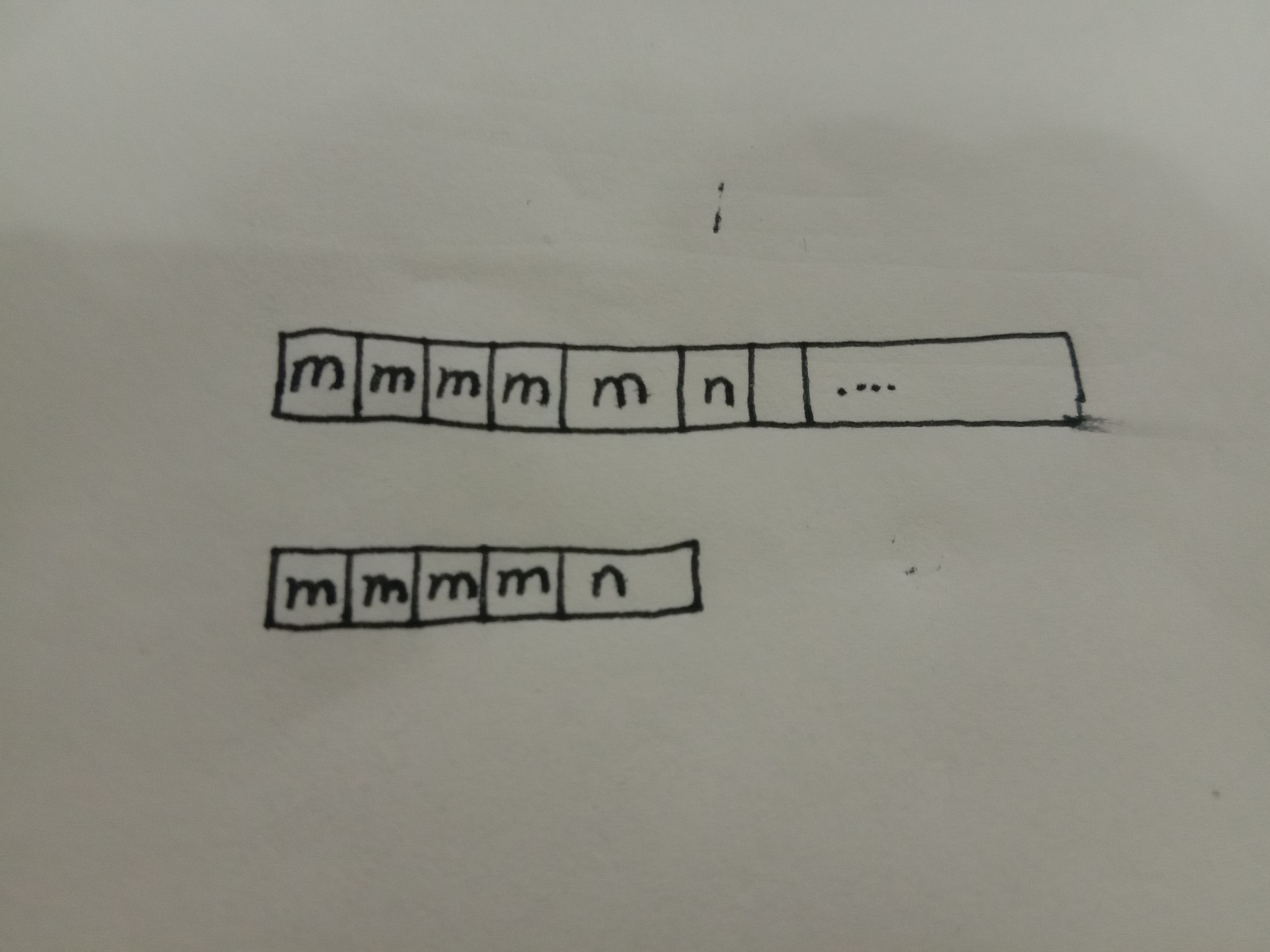
接下来我们来看一种情况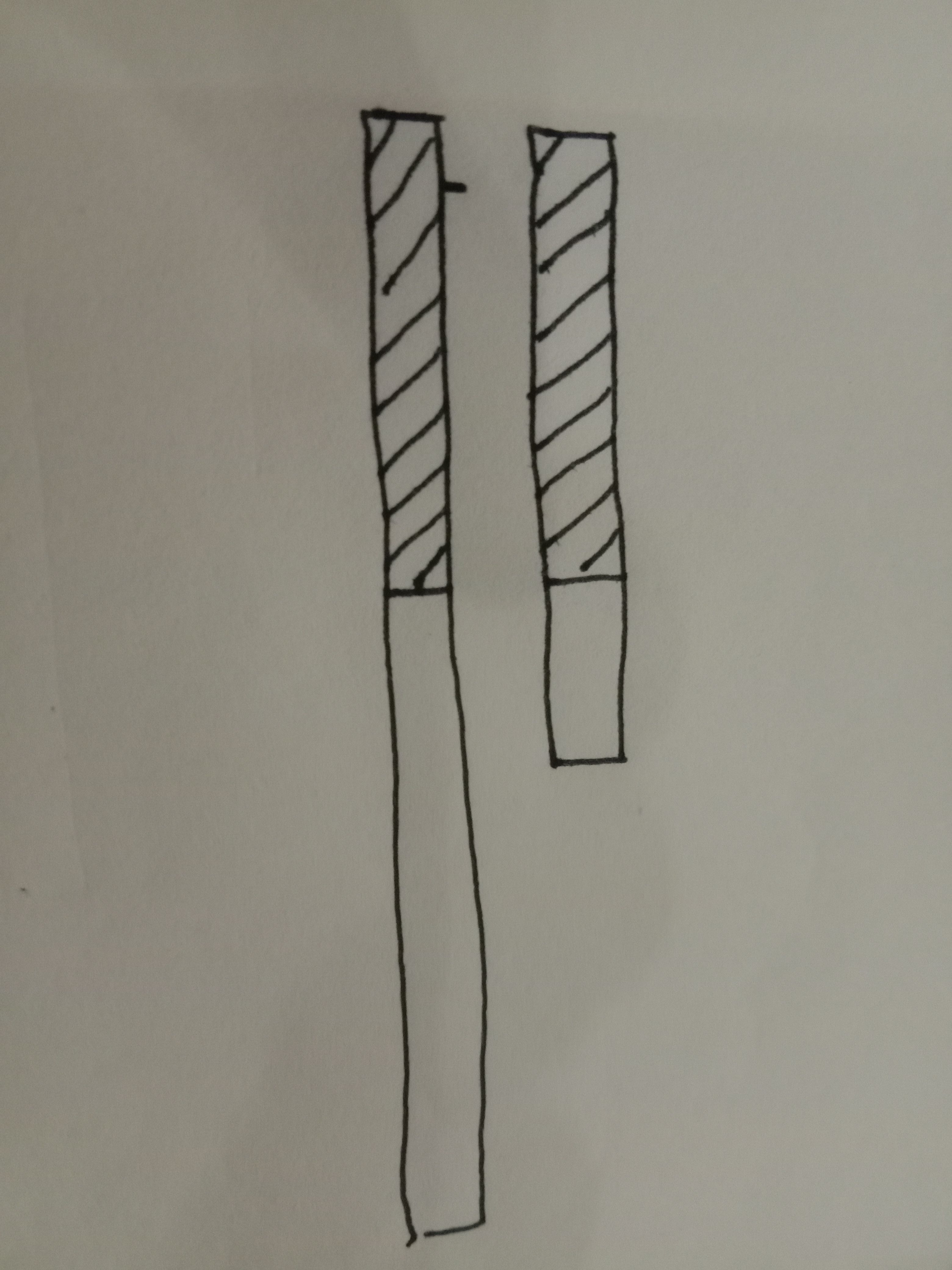
阴影部分表示已经匹配的字符，两段字符串阴影部分后的第一个字符不匹配，
在下一次比较的过程中，我们会从b的阴影部分第二的字符与字符串A开始比较，
上一次比较给我们留下的遗产是 两段阴影部分相同，
有这个条件，黑体字部分可以转化，
在不超过阴影部分的条件下
b的阴影部分第二的字符 等于 a的阴影部分第二的字符
这次比较相当于 a的从第二个字符开始 与 a的从第一个字符开始 进行比较

这个比较是A的自身和自身的比较吧，可以在手里拿到A串后就提前处理，之后的问题如果可以转化成A的自身和自身的比较，我们就能直接O（1）出结果，从而节约了时间，

这里总结这个小发现（和正文分隔）

预处理A的每个点作为起点 与A串的第一个点 开始同时向右划线 ，每次经过的字符都相等的最大长度，
用数组记录下来
数组下标为i的值 表示 A串中 以i这个位置为起点的和以A串第一个字符为起点的
同时往右划线， 能划线的最大长度 （划线以字符不同为结束标志）

下面对从每个点开始和从A串的起点开始的最长匹配长度的结果进行讨论
（也就是带上我们上面发现的那个数组，再去走这个比较的过程）~改进了工具，再次挑战~

这次匹配长度的起点和终点都有一个竖线，
我们关注从第二个字符开始的匹配串的终点
对于A串内每一个起点 我们手里有 1.起点 2.有从这个起点的最长匹配长度（上面提到的那个数组）
有了左端点，还有了长度，那么就能得到右端点

也就是 以这个起点为开始的匹配终点

下面对这个匹配终点，与上一次匹配成功的最大长度在B串中的位置进行比较（我们把匹配成功的部分画上阴影，那么这个就是阴影最后一个位置）

1. 如果这个终点截止在上一次匹配串的终点（阴影部分末端）之前：
   说明这一次匹配比上一次匹配还不成功 匹配的长度比上一次短嘛 （走完A串才算胜利）

我们就能立马知道，以这个点为起点的串是不可能与A完全匹配的

从这一个点得出的结论： 那些匹配终点（通过左端点和长度算出来的右端点）在上一次匹配串的终点（阴影末端）之前的起点都不做考虑 都创业未半 而中道崩殂
而那些换个起点 匹配长度超过 阴影部分最后一个字符的 还留有一丝走完A串长度的可能
于是有了第二种讨论

1. 匹配终点（通过左端点和长度算出来的右端点）截止在阴影部分最后一个字符之后
   这里提一点
   对于 算出来截止在阴影部分内的串的能否走完A的长度这个问题 因为 两端阴影部分完全相同 所以两串的新起点匹配可以转化成A串的提前预处理匹配
   然而对于 算出来截止在阴影部分之后的串能否走完A的长度这个问题 因为阴影后面的匹配情况未知（有可能B的那部分和A的那部分不同对吧）
   就不能转换成A串的提前预处理了

如前面所说 阴影部分之后的点充满未知 虽然好像知道个两段阴影部分之后的第一个点不同 不过那是对阴影的起点的串的匹配来说的 对之后无贡献

至此，小总结：

对于阴影部分内的起点 开头的串
我们能直接算出匹配结果的右端点，
如果这个右端点截止在阴影末端之前 那么这个点不可能完全匹配A串
如果这个右端点截止在阴影末端之后 那么它还有希望完全匹配A串

—我们下面要做的就是把这些还有希望完全匹配A串的点全部都找出来—

要把他们都找出来，其实就是把一类具有共同特征的东西聚到一起，（这句话重点在有共同特征）

那我们就去找这个共同特征啊

这些串共同截止在阴影末端
一个是A的起点开始 一个是阴影部分途中的点作为起点（这个点用C称呼） 长度都是阴影末端下标-C的下标+1
还记得 前面说过的 那个动作吗 一个从a的起点 一个从c点 以同样的速度 向右划横线 能划线的前提是当前字符相同

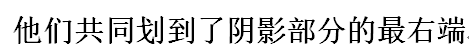
这些串是阴影部分内起点还要有可能走完A全程长度的起点的特征
我的内心从疑惑到沉重到窃喜只用了3秒
我直接预处理都不要了，直接你给我上一次成功匹配的长度，我就立马给你 那些有可能走完A串长度的 起点！
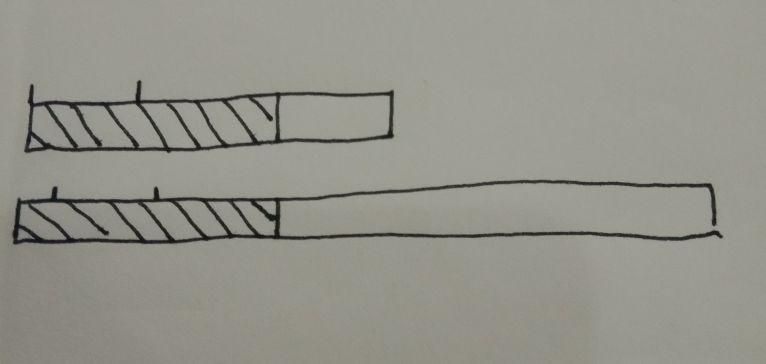
大家集中目光看那个阴影部分的A串

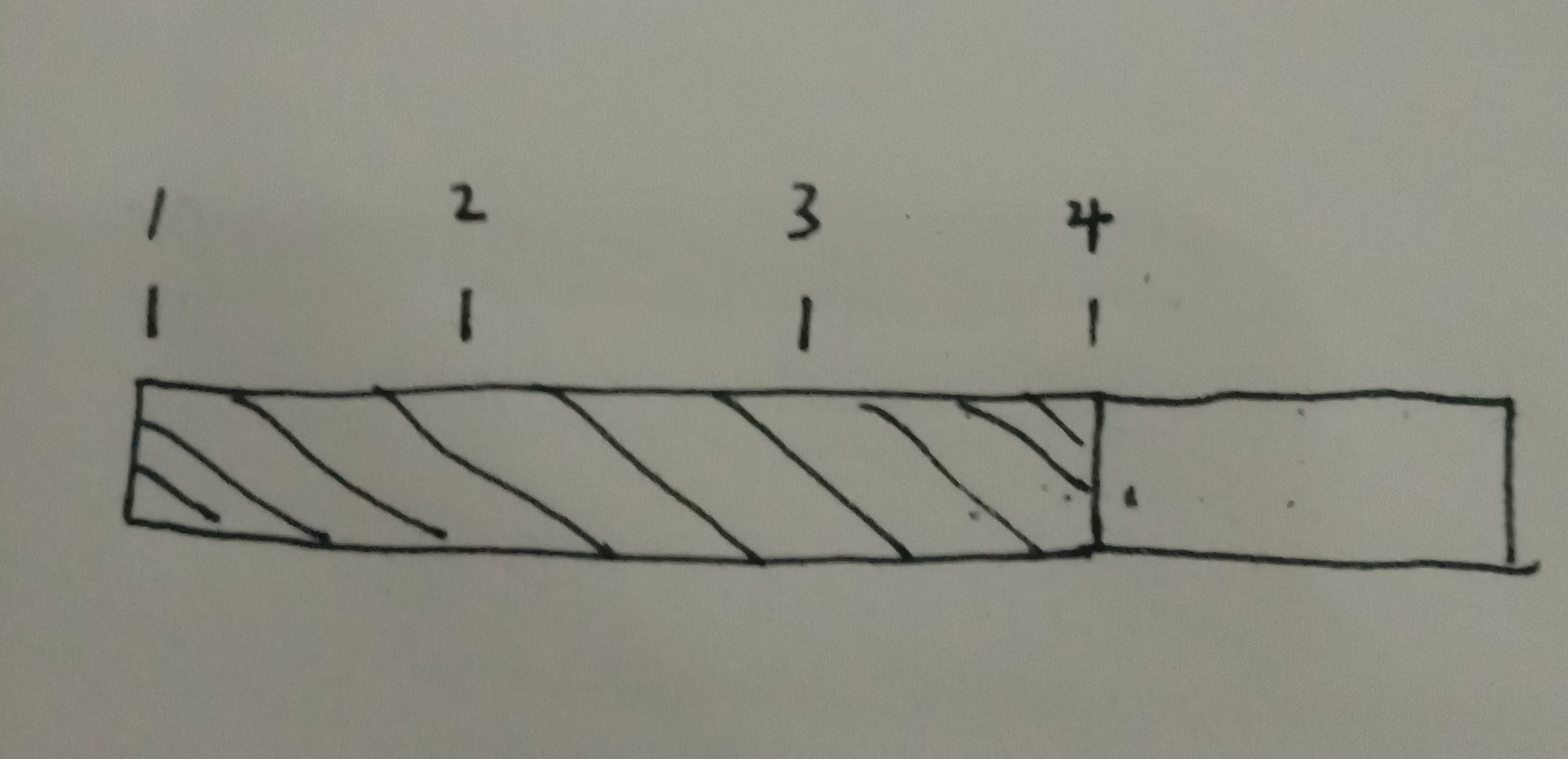
1是A串起点 3是有希望的匹配串的起点 4 为阴影部分终点
我把串1-2称为前缀 串3-4 称为后缀 串1-2 和串3-4如果相等 这个整体叫它 “前缀-后缀-等”
满足这个关系的点 3 就是该长度下 的有成功希望的点
暂时没听懂那我换个解释方法
对于A串的一个前缀串S1
这个S1串内 S1串的一个前缀 和S1串的一个后缀 （当然这俩串长度要相同） 这两个串还相等 （每个位置上对应字符都相同） 满足这些条件的后缀串的起点就是阴影部分内有可能走完A全长的点（有希望的点）

如果一个点和阴影末端的点 形成的串 A串的同样长度前缀串 两个串相同 那么 这就是个有梦想（希望）的点
这些点给他们从阴影部分往后继续枚举 才是有可能成功的
那么问题来了，


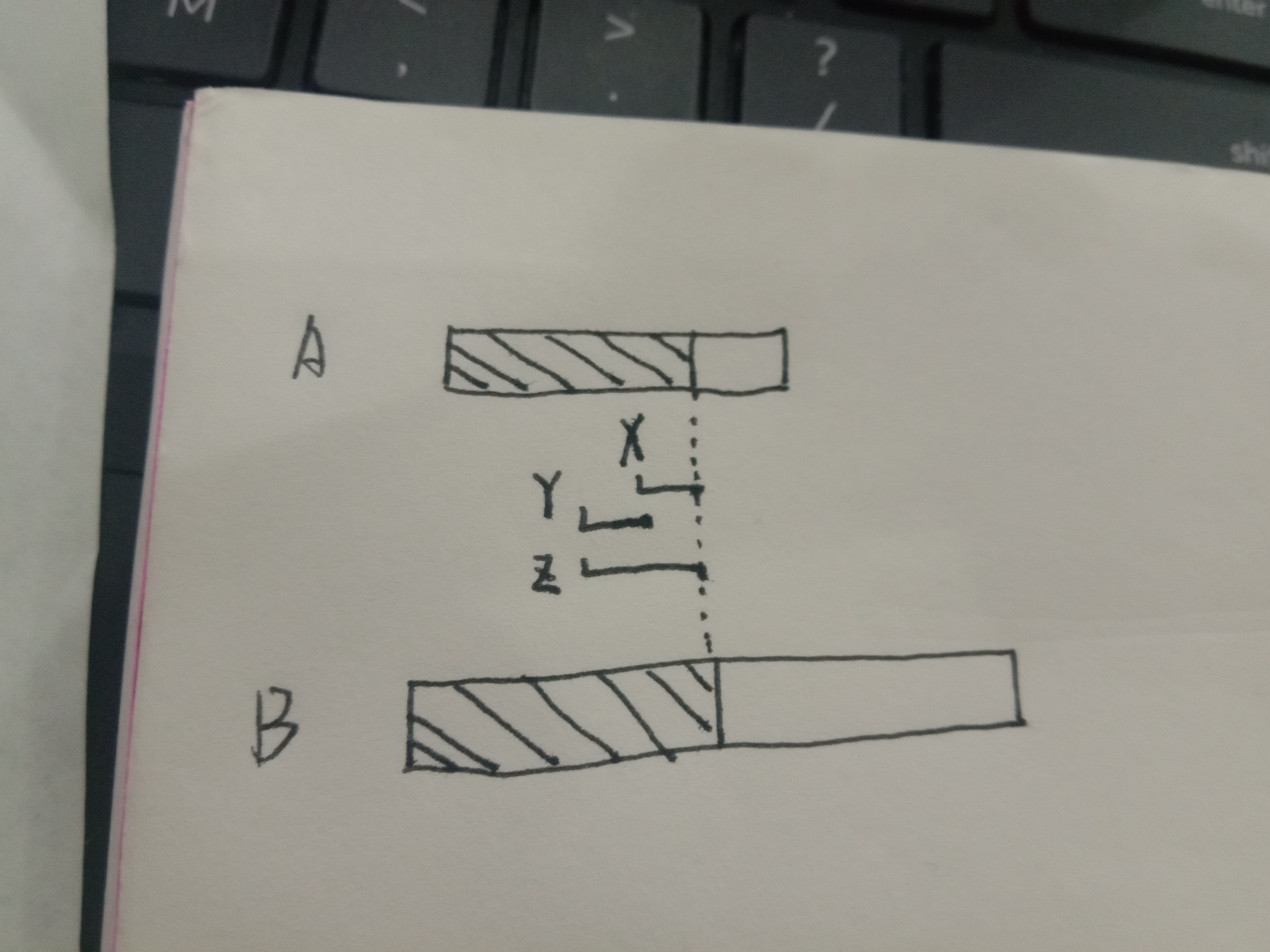
这里X和Z是“有希望的串” 他们的端点x和z是有希望的点
Y是X和Z能推导出来存在的，
Y 和 X 对于Z 构成 “前缀-后缀-等 ”
证明：
x为有希望的串 ，x可作为A串的前缀，Z也是有梦想的串 Z可作为A的前缀 而且Z比X长 ，那么X可作为Z的前缀 Z的和X等长前缀这里叫做Y
回到问题
他俩谁有用？

思想：不知道干什么时，就分类讨论
X和Z都给他们延伸 匹配的机会
这里X和Z对阴影末端后一个字符匹配成功的要求是不同的吧，因为对于原A串的位置不同嘛，
1.下面的分类依据是 长串 短串各自是否匹配成功，
首先得到 长串匹配完要求成功的次数少，这里假设第一种情况长串Z能全部匹配成功，短串X也能匹配成功
也就是说长串Z往后是一整个A串 短串X之后也是一整个A串
阴影之后的对比元素全是B的，距离阴影端点等距的对比元素下标是一样的，

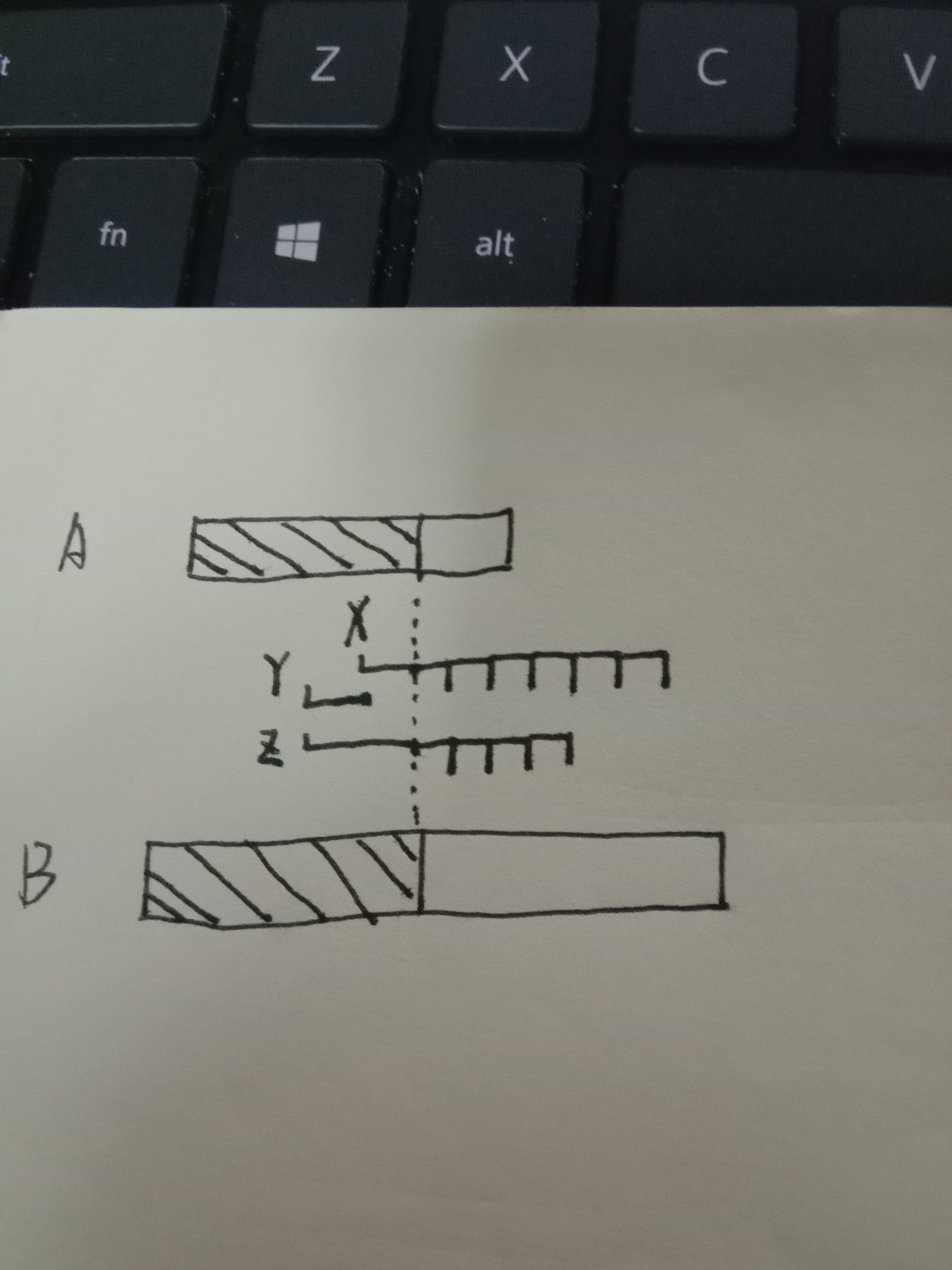
图中像梳子一样的部分是b阴影部分右端点之后的元素
我们可以先匹配长串，长串匹配完了呢，，朴素做法是在当前Z的起点的下一个端点继续匹配，这里我们知道是能优化的吧
找 Z串的“前缀-后缀-等”
而Z串的“前缀后缀等”不难发现就是X串，
那么长串短串都能匹配成功的情况我们给出以下做法
先向后匹配长串，长串匹配成功后，长串的有希望的点就会覆盖短串，短串也能匹配成功的情况就不会遗漏了，
其它情况
1.长串不能匹配成功，短串可以匹配成功
这种情况是不存在的，长串匹配完需要的成功元素比短串少，
2长串匹配成功，短串匹配不成功，
那还是先匹配长串

而匹配长串的过程中又会增加阴影的面积对吧，
这个阴影面积其实能看出来就是朴素比较的长度，每次选取有希望的长串向后匹配的过程中哪怕没有匹配完，但是阴影面积有增加，只要有了上面说的那个工具
B串内每个元素只扫描一遍就完成了整个匹配过程
，这个工具其实就是next数组吧，y总基础课有kmp模板 ，本篇博客重点在于了解kmp算法是怎么来的，