内容一定会更的
今天吧y总的算基的DFS的内容搞定,然后去牛客把那道D题搞定,再从cf上找一道题

一、基本思想

为了求得问题的解，先选择某一种可能情况向前探索；在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索；如此反复进行，直至得到解或证明无解

DFS:优先考虑深度，换句话说就是一条路走到黑，直到无路可走的情况下，才会选择回头，回头也并不是一下回到解放前,是返回到前一步,然后重新选择一条路,如果又到头了继续回头走一步,递归下去.**

联想:肌肉记忆

基本算法1:*
来源:算法基础课题目:排列数字

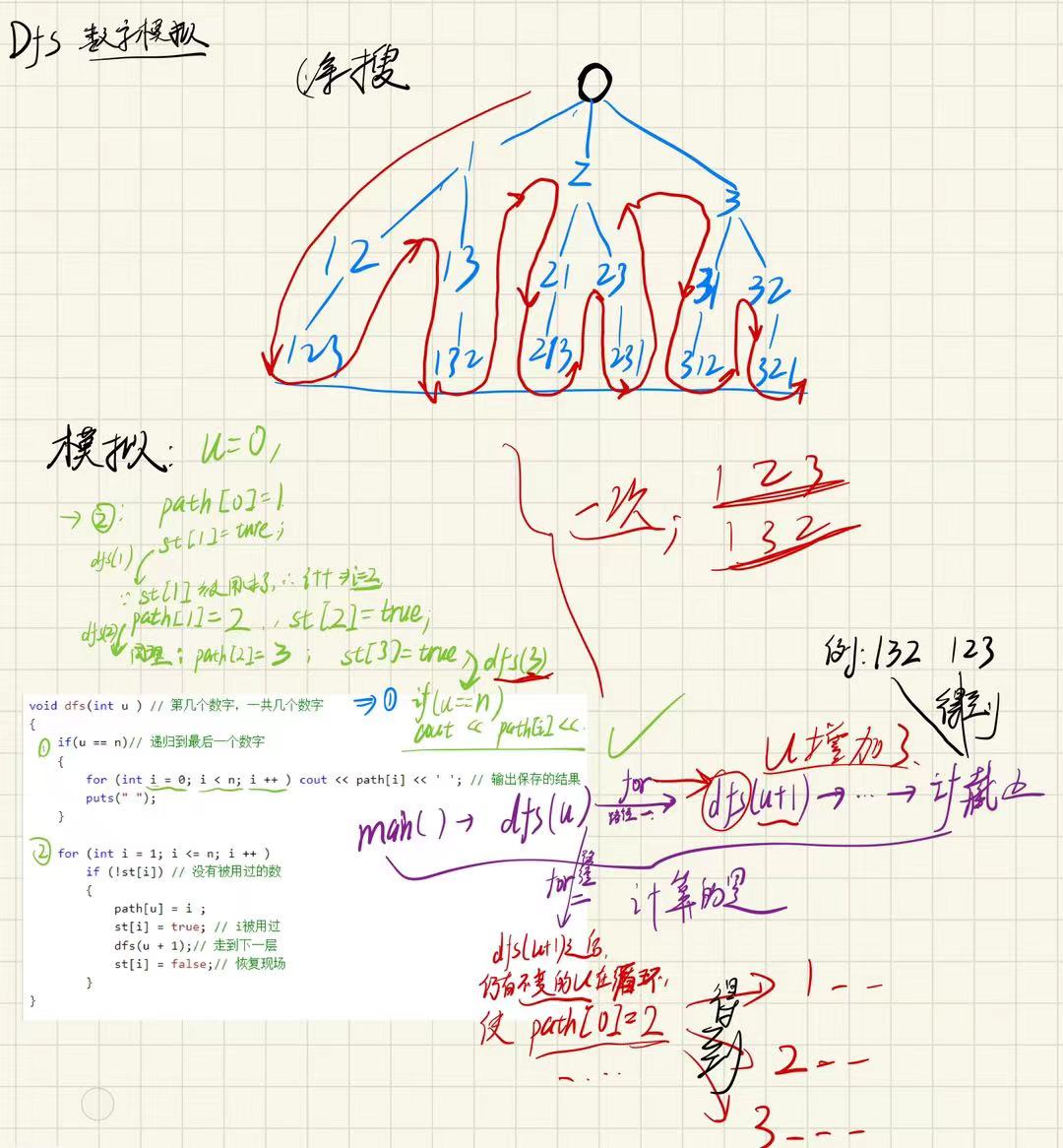
_ 自己模拟一遍,就知道每一步的意义何在 _

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 10;

int n,path[N];
bool st[N];

void dfs(int u)
{
    if(u == n)
    {
        for(int i = 0; i < n ; i++) cout << path[i] << " ";
        puts(" ");
    }

    for(int i = 1 ; i <= n ; i++)
        if(!st[i])
        {
            path[u] = i; 
            st[i] = true;
            dfs(u+1);
            st[i] = false;//为下一次for循环做准备.
        }
}

int main()
{
    cin >> n;

    dfs(0);

    return 0;
}

基本算法2: n皇后问题

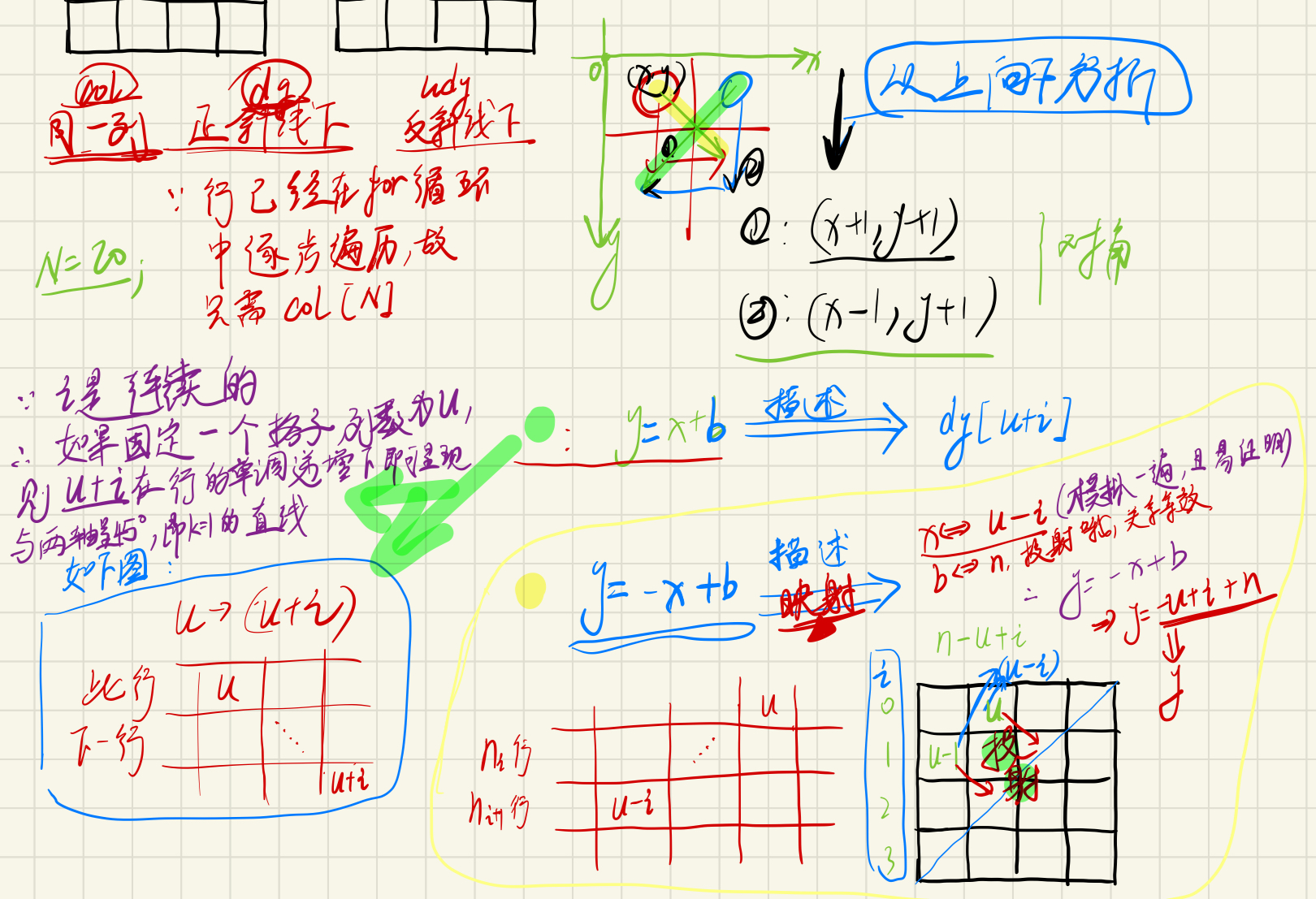
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 20;

int n;
char g[N][N];
bool col[N],dg[N*2],udg[N*2];

void dfs(int u)
{
    if(u == n)
    {
        for(int i = 0 ; i < n ; i++) puts(g[i]);
        puts("");
        return;
    }

    for(int i = 0 ; i < n ; i++)
        if(!col[i] && !dg[u+i] && !udg[n-u+i])
        {
            g[u][i] = 'Q';
            col[i] = dg[u+i] = udg[n-u+i] = true;
            dfs(u+1);
            col[i] = dg[u+i] = udg[n-u+i] = false;
            g[u][i] = '.';
        }
}

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i++)
        for(int j = 0 ; j < n ; j++)
            g[i][j] = '.';

    dfs(0);

    return 0;
}

算法练习题一:

题目链接 >>> https://ac.nowcoder.com/acm/problem/269999
思路:使用深度优先搜索找到每一个可以到(n-1,m-1)的情况,再从中找最小的;
但其实我们可以发现,走过的路径,再走一遍没有任何意义
因为一个for(int i = 0 ; i < 4 ; i++)的dx[i],dy[i]可以将这个点的所有可以移动的情况弄清楚;从一开始就没有漏掉的点,那么这种算法重复到最后,也一定没有漏掉的.再加上st函数来确保自己不走之前走过的点,那么对于d[n-1][m-1]就属于先到先得了,而最小的情况一定是第一个赶到的.

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int,int>PII;
queue<PII> q;

const int N =  1010;

char w[N][N];
int d[N][N];
bool st[N][N];
int dx[4] = {-1,1,0,0},dy[4] =  {0,0,-1,1};
int n,m;

void dfs(int u,int l)
{
    q.push({u,l});
    while(!q.empty())
    {
        auto p = q.front();
        q.pop();
        for(int i = 0 ; i < 4 ; i++)
        {
            int x = p.first + dx[i],y = p.second + dy[i];
            if(w[x][y] != w[p.first][p.second] && !st[x][y] && x >= 0 && x < n && y >= 0 && y < m)
            {
                st[x][y] = true;
                d[x][y] =   d[p.first][p.second]  + 1;
                q.push({x,y});
            }
        }
    }
    if(d[n-1][m-1] == 0) cout << -1 << endl;
    else cout << d[n-1][m-1] << endl;
}

int main()
{
    cin >> n >> m;

    for(int i = 0 ; i < n ; i++)
        for(int j = 0  ; j< m ;  j++)
            cin  >>  w[i][j];

    dfs(0,0);

    return 0;
}

算法练习题二:
出自newcoder >>> https://ac.nowcoder.com/acm/contest/76652/B
这道题呢,操作之前数组的元素的内容已经发生了变化,就相当于:字符类型数组[1,2,3,4],每个元素都是string类型,操作之后变成了[1,12,123,1234]这样.放到二维上同理,既是DP,也是dfs深度搜索.

#include <algorithm>
#include <iostream>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 2000;

char w[N][N];
string s[N];

int main()
{
    int n,m;
    cin >> n >> m;

    for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j++)
            cin >> w[i][j];

    s[1] = w[1][1];
    for(int i = 2 ; i <= m ; i++)
        s[i] = s[i-1] + w[1][i];//行

    for(int i = 2 ; i <= n ; i++)
    {
        s[1] += w[i][1];//列
        for(int j = 2; j <= m ; j++)
            s[j] = min(s[j],s[j-1]) + w[i][j];
    }
    cout << s[m];

    return 0;
}

算法练习题三 : 2018年蓝桥省赛考的DFS题目,考的很简单.
这道题的题意略微难以理解,但理解清楚了问题就不大.
这道题要遍历每一种可能,找每种满足的情况的max值,而满足的情况就是形成闭环.
样例模拟 >>> 2->4 ,4->5,5->3,3->2;这就形成了闭环
题目链接 >>> https://www.lanqiao.cn/problems/182/learning/?page=1&first_category_id=1&second_category_id=3&difficulty=20&tags=DFS

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int N = 100010;
int a[N];
int main()
{
    // 请在此输入您的代码 
    int n; cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    //>>>样例模拟
    // 序号崇拜:3 4 2 5 3 8 4 6 9
    // 样例序号:1 2 3 4 5 6 7 8 9
    int cnt, ans;
    for (int i = 1; i <= n; i++)
    {
        cnt = 1;
        if (a[i] == i) continue;
        else
        {
            int j = i;
            while (a[j] != i)
            {
                j = a[j], cnt++;//构不成闭合回路就是0,从哪来,回到哪.
                //cout << cnt << endl;
                if (cnt > n) {cnt = 1; break;}
            }
        }
        ans = max(cnt, ans);
    }
    cout << ans << endl;
    return 0;
}

算法练习题四:往届蓝桥真题:地宫取宝
题目链接 >>> https://www.lanqiao.cn/problems/216/learning/?page=1&first_category_id=1&tags=DFS
这道题呢,首先要清楚题目表达的真正意思,理解完题目,应该知道你连续拿起的宝物的价值一定是严格单调递增的.
这道题仅仅是两行两列的样例的递归就有点复杂,那么可以去看看链接中蓝桥官网的大佬的作答,如果还是不懂,就考虑用编译器调试一遍,就懂了~

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
int n, m, k;
int p = 1e9 + 7;
int a[55][55];//价值排布
int dp[55][55][15][15];//前两个元素是,访问到的元素;后两个元素,一个是价值数,一个是次数
int dx[] = {1,0};
int dy[] = {0,1};
int dfs(int x,int y,int mx,int cnt)
{
    if(x == n && y == m) return cnt == k;//两种结果,如果cnt == k ,则会返回1,表示结果+1;如果cnt != k,返回0,结果不变.
    if(dp[x][y][mx][cnt] != -1) return dp[x][y][mx][cnt];//dp的记忆化搜索,它的结果的意义与dfs要返回的值相同.
    int res = 0;
    for(int i = 0 ; i < 2 ; i ++)
    {
        int nx = x + dx[i];
        int ny = y + dy[i];
        if(nx < 1 || ny < 1 || nx > n || ny > m) continue;
        if(a[nx][ny] > mx && cnt < k) res = (res + dfs(nx,ny,a[nx][ny],cnt+1))%p;//拿
        res = (res + dfs(nx,ny,mx,cnt))%p;//走到了,但是不买你的账
    }
    return dp[x][y][mx][cnt] = res;//既返回最终答案,也将答案对dp数组赋值.
}
signed main()
{
    memset(dp,-1,sizeof dp);//记忆化访问的东西,最终结果,也就是次数,要对dp数组进行赋值,如果次数是0就重合了
    cin >> n >> m >> k;
    for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j++){ 
            cin >> a[i][j];
            a[i][j]++;
        }
    cout << (dfs(1,1,0,0) + dfs(1,1,a[1][1],1))%p << endl;
    return 0; 
}

算法练习题四: 二进制小数的积
来自cf的一道题,有点简单. >>> https://codeforces.com/contest/1950/problem/D

#include <algorithm>
#include <iostream>
#include <cmath>
#include <bitset>
#include <cstring>
using namespace std;
int n;
void dfs(int x)
{
    if(x <= n)
    {//x的遍历可能不过就几种而已
        while(n % x == 0 && x!=1)
            n/=x;
        dfs(x*10);dfs(x*10 + 1);
    }
    else return;
}
int main()
{
    int t; cin >> t;
    while(t--)
    {
        cin >> n;
        dfs(1);
        if(n == 1) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
    return 0;
}