最小生成树
现在有一个问题就是我们在玩一个游戏,就是要去画图,图上有n个点,我们要用n-1或n条边去连接他们,但是我们连接所用的笔画线是有不同损耗的!我们要如何去找到这个最小代价的画法?我们当然会选择最小代价对路径去连接它,这个要用最小生成树!
首先我们来了解一下什么是最小生成树:
最小生成树是一副连通加权无向图中一棵权值最小的生成树。画一个图:
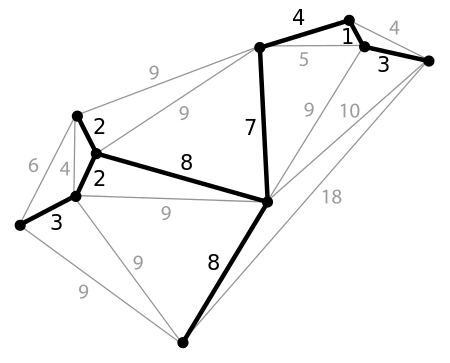
一个平面图和它的最小生成树。在该图中,边的长度正比于权值A。
我们可以看到这个图的最小生成树有两个归并方向,一个是边+权,另一个是点+权!所以我们去求最小生成树就有两种方法—Kruskal(边)和Prim算法(点)
下面我们来看一下这两个算法!
Prim–点
此算法可以称为“加点法”,每次遍历选择代价最小的边对应的点,加入到最小生成树数组中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。是不是感觉他与Dijkstra算法思路有相似之处?
图的所有顶点集合为g;初始令集合u={A},v=g−u;在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组st,用来维护集合v中每个顶点与集合u中最小代价边信息:
简单来说就是我们线初始化一个dist数组,然后我们去遍历他!找到一个集合外最近的点t,然后再用t去更新其他点到集合的距离,然后改变他的状态!
看着太过于麻烦!所以我们来看图:
我们来举一个例子:
1.看下面的连接图:
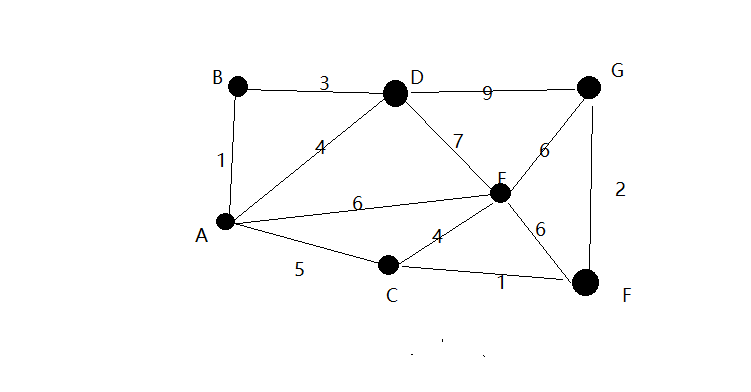
2.我们选A为起始点,A到B,D,C,E的距离最小为A–>B=1,所以我们连接B点.
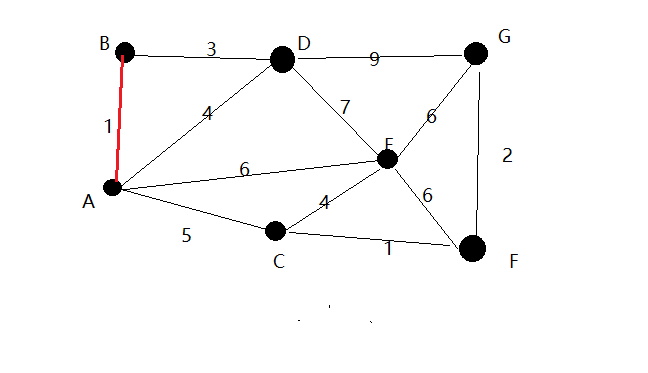
3.下面我们来搜索距离A,B权重最小的点,我们可以找到B–>D=3最小,所以我们连接D点:
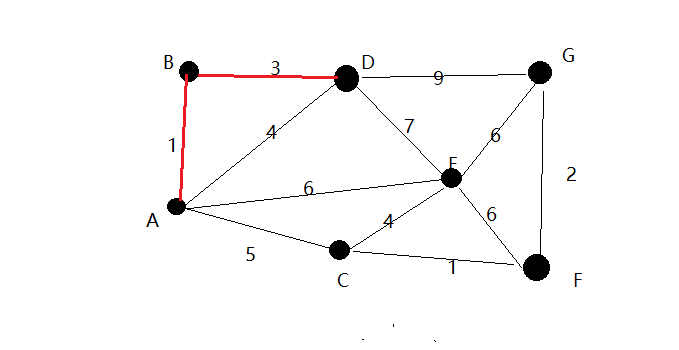
4.遍历寻找距离A,B,D权重的点,我们可以找到A–>C=5最短,连接C点!
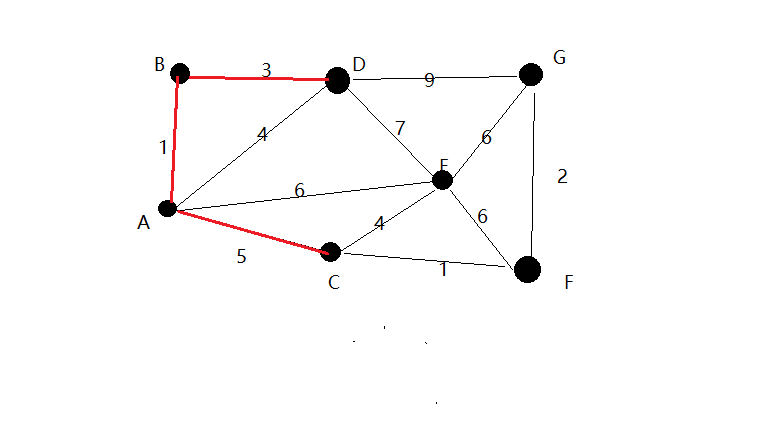
5.算法继续重复上面的步骤。距离C为1的顶点F被话红线连接表示。
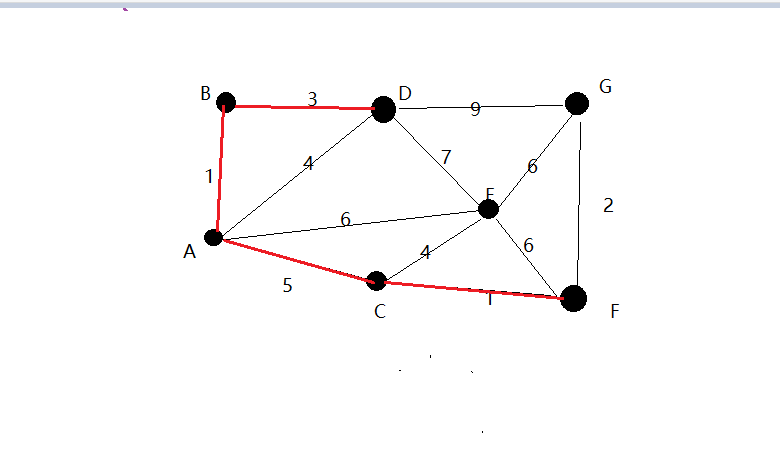
6.在当前情况下,可以在E与G间进行选择。G距F为2最近,因此将顶点G与相应边FG画线表示。
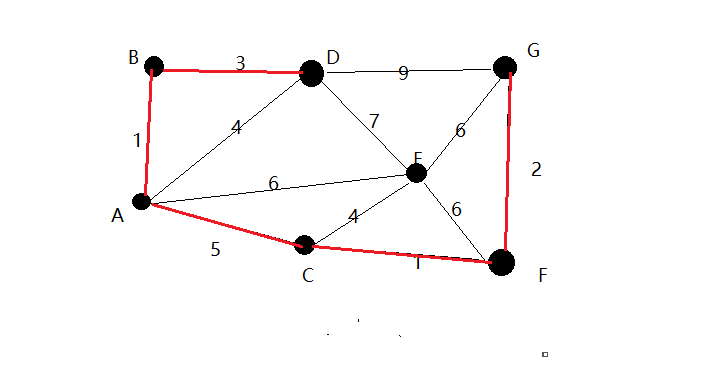
7.当前看E距离谁最近连接!
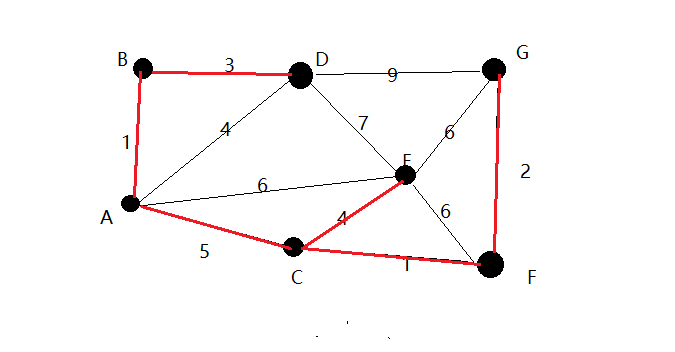
8.现在,所有顶点均已被选取,图中即为连通图的最小生成树。在此例中,最小生成树的权值之和为16。
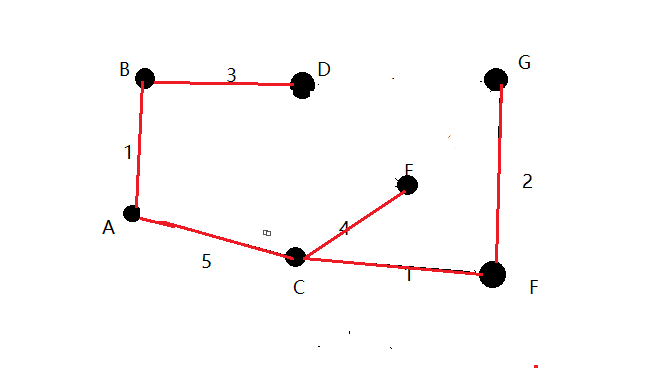
这个就是prim算法的图解
例题
对于图论问题,我建议去理解别人是如何创建图的!其余的都是一个过程模拟!
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=510,INF=0x3f3f3f3f;
int n,m;
int g[N][N];
//读入连接图
int dist[N];
//存储距离用的数组
bool st[N];
//访问状态
int prim(){
//初始化,方便取最小值
memset(dist,0x3f,sizeof dist);
//代价和
int res=0;
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++)//寻找最小边
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
//如果不存在
if(i&&dist[t]==INF) return INF;
//如果是最小边
if(i)res+=dist[t];
//存储到数组中
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],g[t][j]);
//标记已经访问
st[t]=true;
}
return res;
}
int main(){
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--){
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);//无向图有可能有自环与重边的问题
}
int t =prim();
if(t==INF)cout<<"impossible"<<endl;
else cout<<t<<endl;
return 0;
}
当然我们因为有推入推出的操作,所以我们可以用堆优化!由于优化版不太常用,所以我们这里不做过多的介绍!有兴趣的童鞋可以去看一下dijkstra的优化!
Kruskal——边
此算法可以称为“加边法”,初始最小生成树边数为0,每遍历一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。对于图我们不一定要用邻近表来存储或其他的数据结构,用结构体就好了!!
1. 把图中的所有边按权重从小到大排序(STL快乐);
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大枚举边,所选的边连接的两个顶点ui,vi如果不连通,则将它们成为最小生成树集合的一条边(并查集的思想),并将这两颗树合并作为一颗树。)
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
我们来看一个实例:
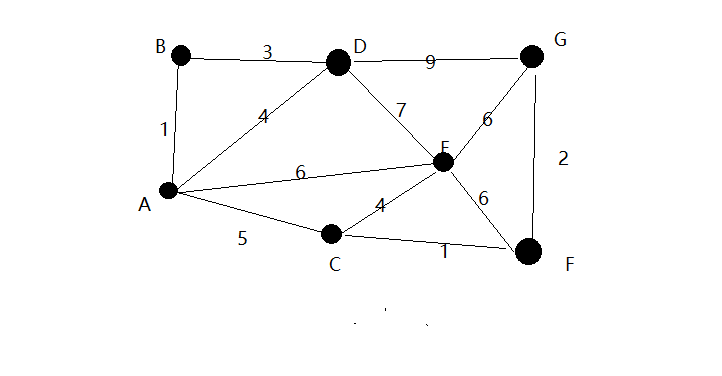
1.首先第一步,我们有一张读入图g,有若干点和边
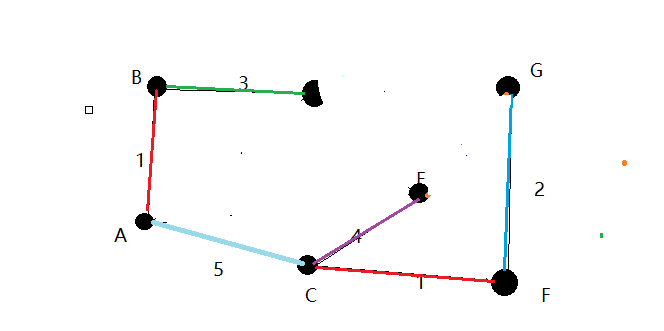
2.将所有的边的长度排序,用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。对自己最好情况的排序,对局部最优的资源进行选择,排序完成后,我们率先选择了边AB,CF。这样我们的图就变成了下图
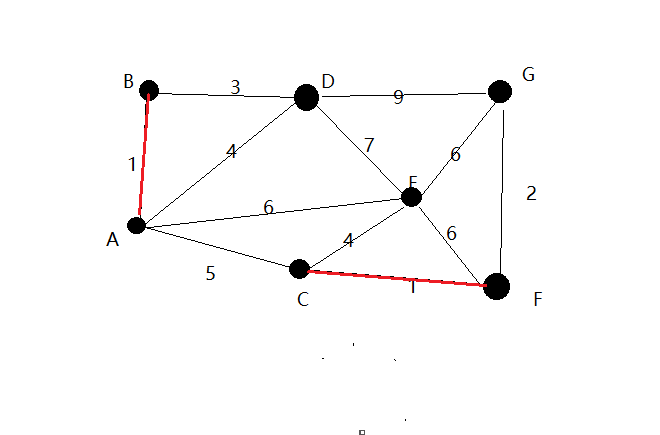
3.在剩下的边中寻找。我们找到了GF。这里边的权重也是2
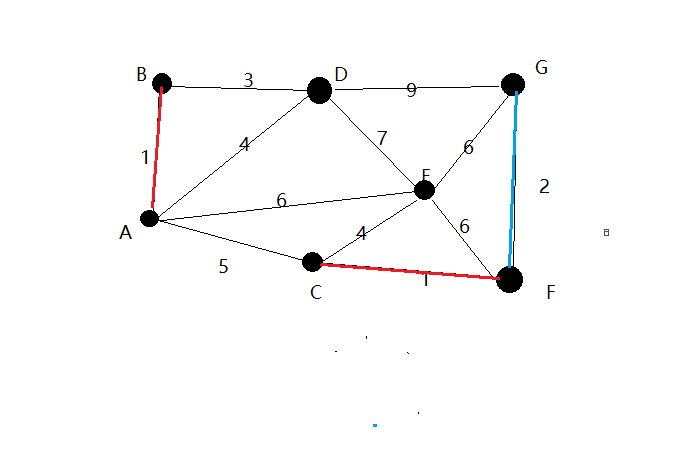
4.继续遍历!
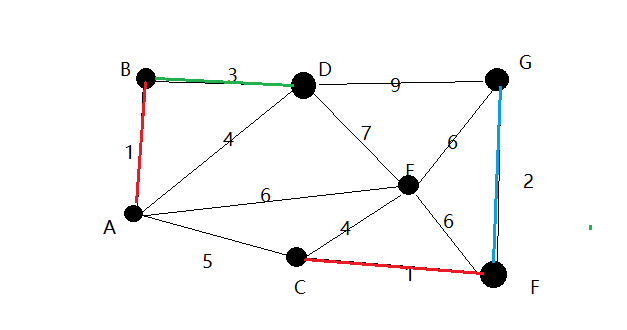
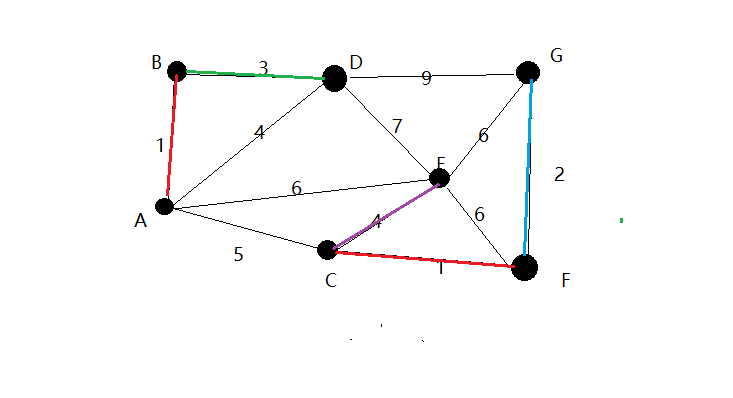
5.在这种情况下!由于有环,所以我们要连接CE边!
6.依次类推我们找到了5,即AC。
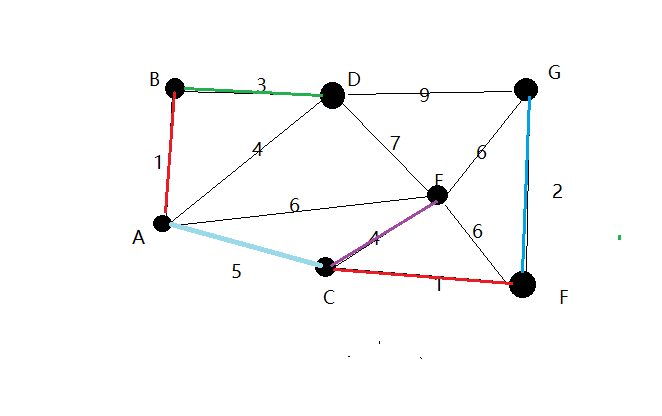
7.现在,所有点均已被边连接,图中即为连通图的最小生成树。在此例中,最小生成树的权值之和为16。
例题
例题链接
代码:
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010,M=200010,INF=0x3f3f3f3f;
int n,m;
int p[N];
struct Edge{
int a,b,w;
bool operator<(const Edge &W)const
{
return w<W.w;
}
}edges[M];
int find(int x){
if(p[x]!=x)p[x]=find(p[x]);
return p[x];
}
int kruskal(){
sort(edges,edges+m);
//初始化
for(int i=1;i<=n;i++)p[i]=i;
int res=0,cnt=0;
//cnt边数,res代表权重和
for(int i=0;i<m;i++){
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
a=find(a),b=find(b);
//如果不连通
if(a!=b){
p[a]=b;//合并
res+=w;
cnt++;
}
}
//不连通
if(cnt<n-1)return INF;
return res;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++)
{
int a,b,w;
cin>>a>>b>>w;
edges[i]={a,b,w};
}
int t=kruskal();
if(t==INF)cout<<"impossible"<<endl;
else cout<<t<<endl;
return 0;
}
体现并查集模板的代码:
(如果你不熟悉,或者没有学过并查集那么我这里有新手指南和熟悉强化秘法)
—> 并查集
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+10, M = 2e5+10, INF = 0x3f3f3f3f;
int n, m;
int p[N];//祖宗节点
struct Edge {
int u, v, w;
bool operator < (const Edge & T) const {
return w < T.w;
}
}edges[M];
int find(int x) {
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal() {
sort(edges, edges+m);
for(int i = 1; i <= n; i++) p[i] = i; //初始化并查集
int res = 0, cnt = 0;
//res 最小生成树中的权重之和
//cnt 当前加了多少条边
for(int i = 0; i < m; i++) {
auto t = edges[i];
t.u = find(t.u), t.v = find(t.v);
if(t.u != t.v) {
p[t.u] = t.v;
res += t.w;
cnt++;
}
}
if(cnt < n - 1) return INF;
return res;
}
int main() {
cin >> n >> m;
int u, v, w;
for(int i = 0; i < m; i++) {
cin >> u >> v >> w;
edges[i] = {u, v, w};
}
int x = kruskal();
if(x > INF/2) puts("impossible");
else cout << x << endl;
}
小结
其实,求最小生成树有两个要点,一个是权值最小,还有一个就是这个图必须是树。而Prim和Kruskal的不同之处在于两者选择的变量不同,Prim选择的是始终保持权值最小,然后逐个加点构建一棵树。而Kruskal则是始终保证是一棵树(虽然构建过程中不一定是真正的树,但并查集判环可以这样理解:是为了保证结果是一颗树),然后逐条加边,使权值最小。这个就是最小生成树的理解,由于时间复杂度yxc老师模板上有,我这里不做过多的分析!当然如果你对dijkstra与并查集熟悉(熟悉是指:可以解决相关题目,不是你知道它是什么,它能干什么!)!由于最近夏令营时间原因所以图文解释不好,有任何问题请私聊我!最后模板是用来理解的,记住它是一个过程,不去背它又是一个过程!理解比不上动手!!好了!这就是最小生成树的基础知识,谢谢你的阅读!希望你有所收获!
yxc老师的模板 链接
朴素版prim算法
时间复杂度是 O(n2+m)O(n2+m), nn 表示点数,mm 表示边数
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal算法
时间复杂度是 O(mlogm)O(mlogm), nn 表示点数,mm 表示边数
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
作者:yxc
链接:https://www.acwing.com/blog/content/405/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。


我看有的是题是 N - 1次,有的是N次,弄得很迷
因为连接n个点,需要n-1条边
循环 n 次是不是为了确定每个点是不是可以存在于树中?
对
好的,thank you
客气 ,yls那个视频讲的很好,建议二刷
hhh,我不知道是哪个,qwq,能发个链接吗?hh
想问一下,prim算法中最外层循环为啥是 N 次,不是 N - 1次呢?
超棒!图论都是跟着你写的总结学的😂
hhhh 马上就写图论三了
棒!
棒棒哒!
谢谢 hhhh
很棒!
谢谢 hh