今天一整天都是水过去的哇哇,搞了个十分简单的二叉树重构,嗯嗯嗯,正在准备初赛的朋友们应该会复习到这个,不过不难不难啊,憋慌哟。
话说回来,距离noip,还剩…不说了,说多了都是泪。
学习笔记献上,请放心食用。/微笑/微笑/微笑
嗷嗷嗷嗷最后不到两个月冲刺了!!!
我们的问题是:
- 给出一棵二叉树的先序遍历与中序遍历,如何构建出这棵二叉树呢?

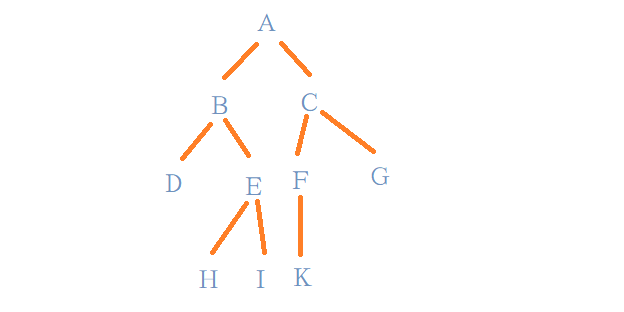
我们知道,二叉树的先序遍历遍历的第一个点一定是根节点,所以根节点一定是$A$。

在中序遍历中,根节点一定是在最中间的,所以中序遍历中A左边的节点都在$A$的左子树上,右边的节点都在$A$的右子树上。
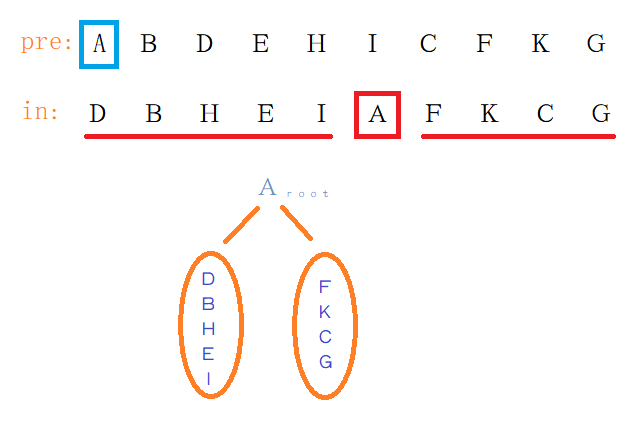
那么我们就衍生出了一个子问题:
若有一棵二叉树,先序遍历为:$B D E H I$,中序遍历为:$D B H E I$,构建出的是什么样的二叉树。而这课构建出来的二叉树就是$A$节点的左子树。
显然,$A$节点左子树的根节点是$B$节点,而$B$节点的左节点是$D$,右子树包括节点$H、E 、I$,且我们知道右子树的先序遍历与中序遍历。
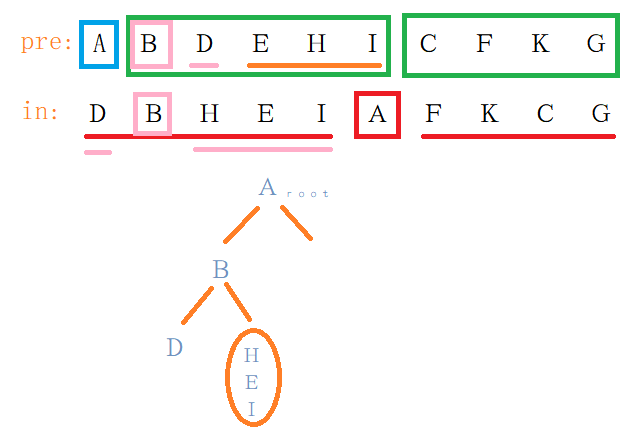
接着我们构建$B$节点的右子树,明显可见根节点为$E$,$E$的左节点为$H$,右节点为$I$。
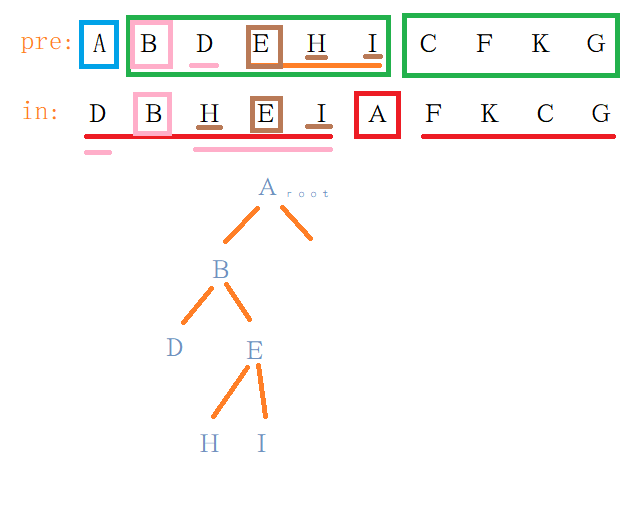
同样的,我们可以构建出$A$节点的右子树为:
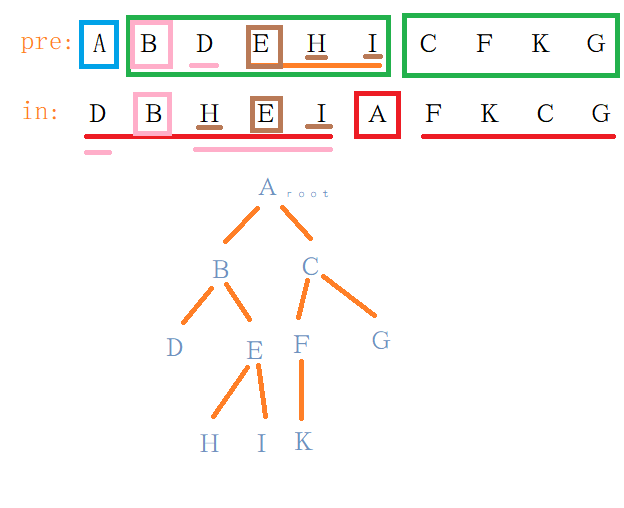
所以最后构建出来的二叉树就是:


写的很好,很清晰,不过还有一种类似的题目是,给前序和后序,判断所有的可能解。