历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

【学习笔记】超简单的快速傅里叶变换（FFT）（含全套证明）

作者：

繁凡さん , 2021-01-02 08:54:35 , 所有人可见 , 阅读 7730

13

20

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

来了来了，总算来了，y总的进阶课总算是来到了数学专题，我等FFT等了好久了，等得我都已经学会了y总才讲到hhh

点我看多项式全家桶(●^◡^●)

~~学习笔记（用ipad记录的笔记）~~

超级简单的快速傅里叶变换！只要基础够扎实，顺着推一遍没有什么难以理解的，我学的整个过程没有一点卡壳，真的很爽，整整写了三个多小时，写了满满6页的笔记。主要是内容太多了。又花了几个小时的时间整理整个过程，梳理出这篇博客，一万字有余。

我的数学博客一般都会包含全套证明，没有证明我会很难受的hhh。

一、概念概述

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

离散傅里叶变换（Discrete Fourier Transform，缩写为 DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其 DTFT 的频域采样。

FFT 是一种高效实现 DFT 的算法，称为快速傅立叶变换（Fast Fourier Transform，FFT）。它对傅里叶变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。快速数论变换 (NTT) 是快速傅里叶变换（FFT）在数论基础上的实现。

在 1965 年，Cooley 和 Tukey 发表了快速傅里叶变换算法。事实上 FFT 早在这之前就被发现过了，但是在当时现代计算机并未问世，人们没有意识到 FFT 的重要性。一些调查者认为 FFT 是由 Runge 和 König 在 1924 年发现的。但事实上高斯早在 1805 年就发明了这个算法，但一直没有发表。

~~上述内容摘自百度hhh~~

就是想让大家了解一下我们将要学的东西到底有多🐂🍺(●’◡’●)。然后进入我们今天的正题：

二、前置知识

首先是一些基础概念：

1. 多项式

学习笔记

2. 复数

在这里插入图片描述

复数乘法：

两个复数 $z_1 = a_1 + b_1i,~z_2 = a_2 + b_2 i$ 相乘的结果为

$$z_0~=~z_1 \times z_2~=~(a_1 + b_1i) \times (a_2 + b_2i) = a_1a_2 + a_1b_2i + a_2b_1i + b_1b_2i^2$$
又因为 $i^2 = -1$

所以

$z_0~=~(a_1a_2 - b_1b_2) + (a_1b_2 + a_2b_1) i$

在复平面上，$z_1,~z_2,~z_0$ 所对应的幅角 $\theta_1,~\theta_2,~\theta_0$

有如下关系：

$\theta_0 = \theta_1 + \theta_2$

他们的模有如下关系$|z_0| = |z_1| \times |z_2|$

考虑 $z = a + b_iz$ 和它的共轭复数 $\overline z = a - bi$有

$$z \times \overline z~=~(a + bi) \times (a - bi) = a^2 + b^2$$
因此两个互为共轭复数的数之积一定是一个实数。

复数除法：

对于两个复数 $z_1 = a_1 + b_1i,~z_2 = a_2 + b_2 i$，他们相除的结果为

$$z_0 = \frac{z_1}{z_2}$$

考虑分数上下同时乘 $\overline{z_2}$ ，有

$$z_0~=~\frac{z_1 \overline {z_2}}{a_2^2 + b_2^2}$$

分母是一个实数，可以直接将分子的实部虚部除以分母。

复数指数幂：

有欧拉公式

$$e^{i\theta} = \cos \theta + i \sin \theta$$
其中 $e$ 是自然对数的底数

当取 $\theta = \pi$ 时，有

$$e^{i\pi} = \cos \pi + i \sin \pi$$
又因为 $$\cos \pi = 1,~sin \pi = 0$$

所以

$$e^{i\pi} = -1$$

也就是

$$e^{i\pi}+1=0$$

欧拉公式，上帝公式！

3. 复数的单位根 / 单位向量

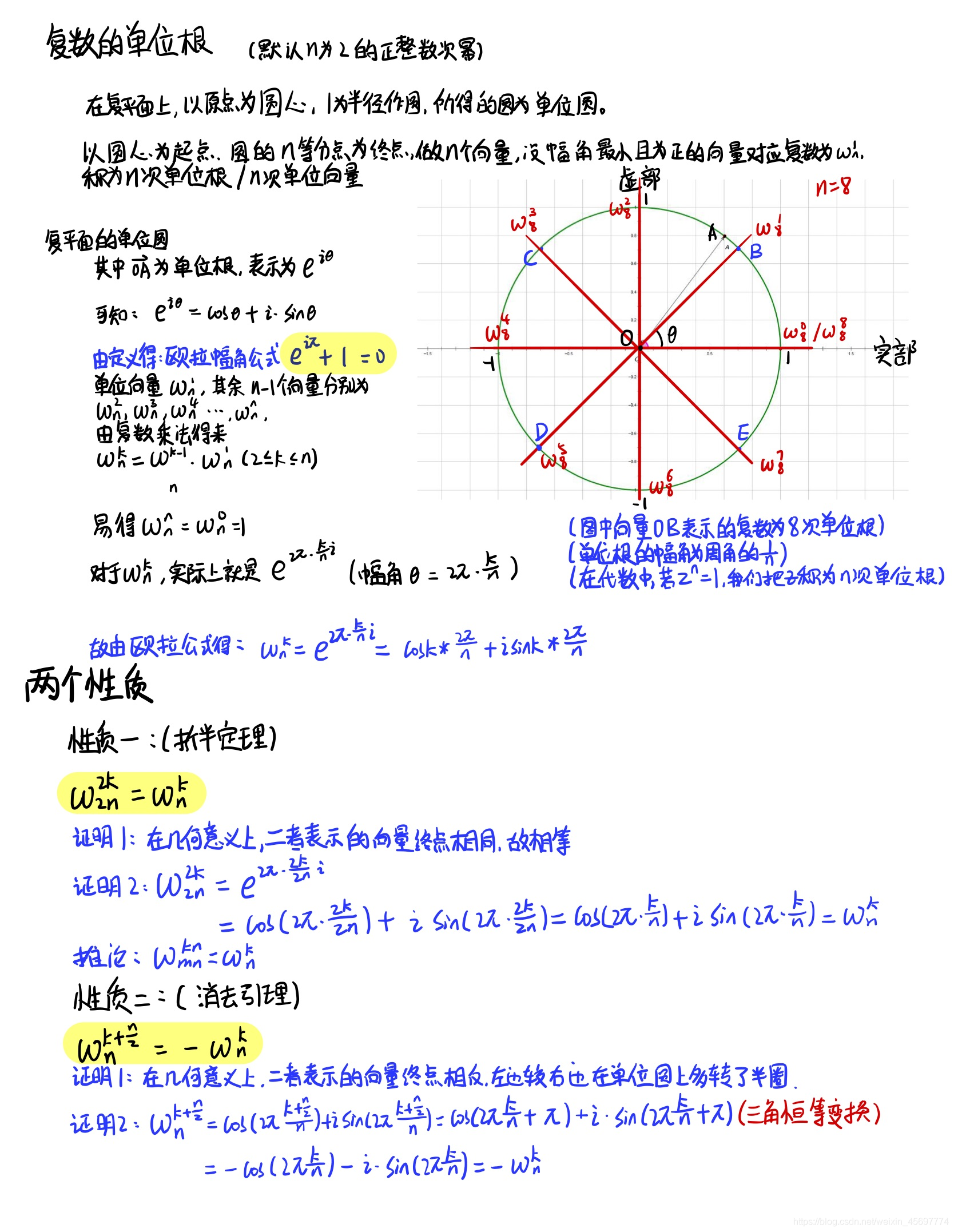
在这里插入图片描述

三、FFT 算法概述

考虑对两个多项式做乘法，如果运用系数表示法，显然需要 $O(n^2)$ 的时间复杂度，而如果已知两个多项式的点值表示法，则只需要 $O(n)$ 的时间复杂度。因为只需要将对应的点值纵坐标相乘就可以了。

但是我们将一个多项式从系数表示法改为点值表示法（称为求值）需要 $O(n^2)$的复杂度（因为每个横坐标都需要 $O(n)$ 的时间去计算），而将一个点值表示法改为系数表示法（称为插值）则需要 $O(n^3)$ 的复杂度来做高斯消元。但是只要我们将这两步都优化至低于 $O(n^2)$的复杂度，就可以得到一个比直接用系数表示法乘更优的做法。

而求出一个 $n$ 次多项式在每个 $n$ 次单位根下的点值的过程，被称为离散傅里叶变换$\tt (Discrete\ Fourier\ Transform\ ,\ DFT)$，而将这些点值重新插值成系数表示法的过程，叫做离散傅里叶逆变换$\tt (Inverse\ Discrete\ Fourier \ Transform\ ,\ IDFT)$。

下面均设将要进行变换的多项式为 $(n - 1)$次多项式 $A(x) = \sum_{i = 0}^{n - 1} a_i \times x^i$ 。其中 $n$ 是 $2$ 的整数幂。如果不是的话，则向 $A(x)$ 的更高次数位 $n$ 补充 $a_n = 0$ ，令其成为 $n$ 次多项式，一直进行直到其次数$+1$的值是 $2$ 的整数幂，取 $n$ 等于其次数，$m = \frac{n}{2}$ 。

四、离散傅里叶变换（DFT）

在这里插入图片描述

考虑求出一个长度为 n 数列 $\{d_i\}$，这个数列的第 k 项为 $A(x)$在 $n$ 次单位根的 $k$ 次幂处的点值。

因此有

$$d_k~=~\sum_{i = 0}^{n - 1} a_i \times \omega_{n}^i$$

注意上式中的 i 为$\Sigma$ 循环的循环变量，而不是 -1 的二次方根。

这个过程是 $O(n^2)$ 的，我们考虑使用 快速傅里叶变换$\tt (Fast \ Fourier \ Transform\ ,\ FFT)$ 来优化这个过程。

五、快速傅里叶变换（FFT）

在这里插入图片描述

六、离散傅里叶逆变换（IDTF）

至此，我们已经有了 $O(n \log n)$的算法来计算两个系数表示法的多项式相乘后的点值表示。接下来我们只需要用 $O(n \log n)$ 的时间复杂度完成插值的过程，就可以得到一个完整的 $O(n \log n)$ 的系数型多项式乘法算法了。

我们目前已知一个 $(n - 1)$ 次多项式 $A(x)~=~\sum_{i = 0}^{n - 1} a_i x^i$ 进行了离散傅里叶变换后的点值 $\{d_i\}$，即

$$d_k~=~\sum_{i = 0}^{n - 1} a_i \times \omega_n^{ik}$$

现在试图还原系数数列 $\{a_i\}$。

结论：

$$a_k~=~\frac{1}{n} \sum_{i = 0}^{n - 1} d_i \omega_n^{-ki}$$

下面是证明
在这里插入图片描述

上述变换是 DFT 的逆变换，称为 IDFT。我们可以通过这个式子求出这个多项式的系数表示法。

七、快速傅里叶逆变换（IFFT）

下面最后的问题就是如何用较低的复杂度计算 $B(x)~=~\sum_{i = 0}^{n - 1} b_i \times x^iB$

在 $w_n^{-ki}$ ，其中 $0 \leq k < n$ 处的点值。

而 $w_n^{-k}$ 可以看做 $n$ 次本原单位根每次逆时针旋转本原单位根幅角的弧度，因此$\omega_n^{-k}$ 和 $\omega_n^k$是一一对应的。具体的，$w_n^{-k} = w_n^{k + n}$ 。因此我们只需要使用 FFT 的方法，求出 $B(x)B$ 在 $\omega_n$ 各个幂次下的值，然后数组反过来，即令 $a_k~=~\frac{1}{n} \sum_{i = 0}^n B(w_n^{n - k})$ 即可。

这一步快速计算插值的过程叫做快速傅里叶逆变换$\tt (Inverse\ Fast\ Fourier\ Transform\ ,\ IFFT)$。

至此，我们得到了一个时间复杂度为 $O(n \log n)$ 的多项式乘法计算方法。

八、FFT算法整体流程

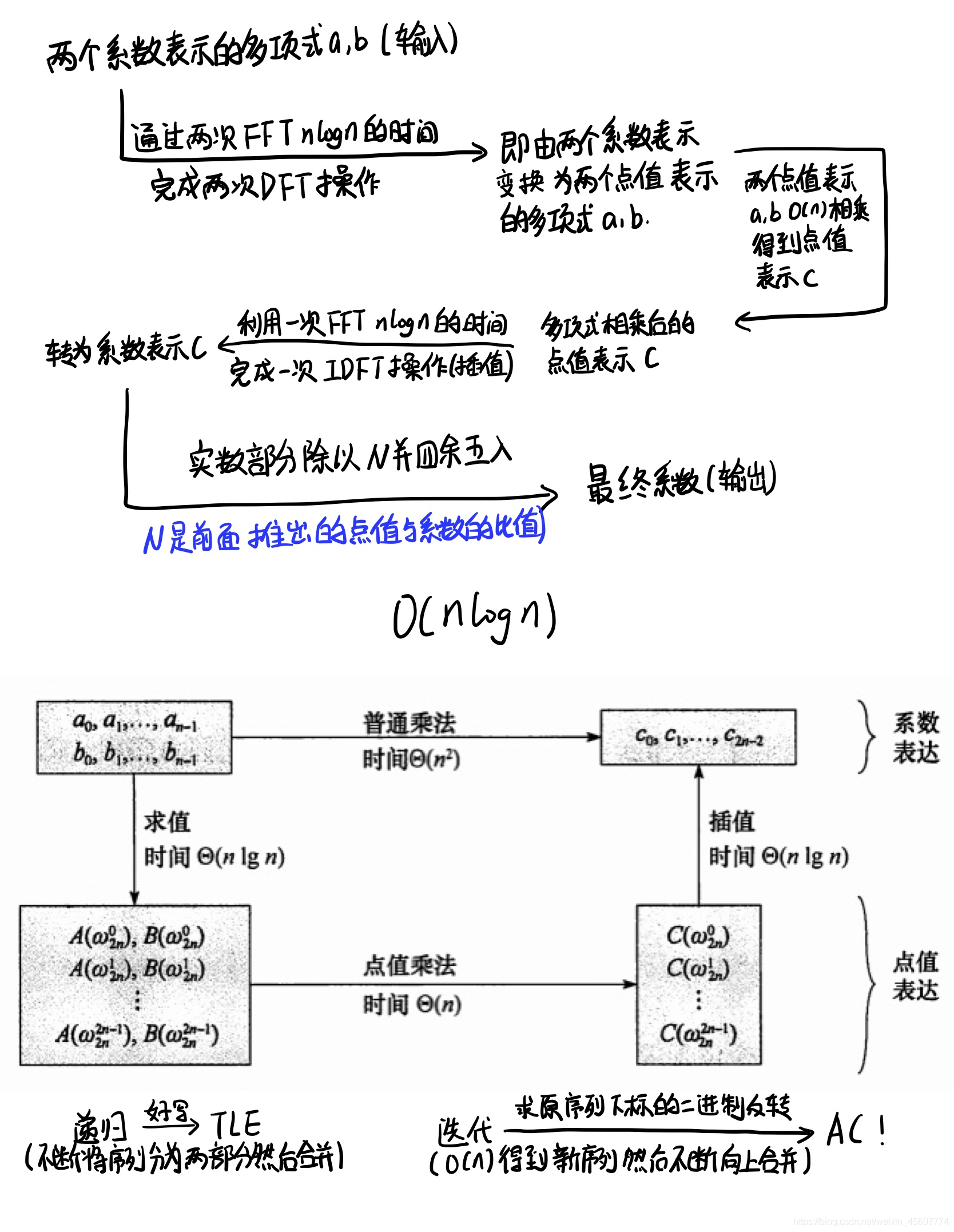
在这里插入图片描述

九、代码实现

1. 递归版

我们把上述的思路实现用递归可以很形象地实现FFT函数。

这里要注意一下，尽管C++自带有复数库，但是建议手写一下，代码不长，手写常数小。

struct Complex
{
    double x, y;
    Complex (double x = 0, double y = 0) : x(x), y(y) { }
}A[N], B[N];
Complex operator * (Complex J, Complex Q) {
    //模长相乘，幅度相加
    return Complex(J.x * Q.x - J.y * Q.y, J.x * Q.y + J.y * Q.x);
}
Complex operator - (Complex J, Complex Q) {
    return Complex(J.x - Q.x, J.y - Q.y);
}
Complex operator + (Complex J, Complex Q) {
    return Complex(J.x + Q.x, J.y + Q.y);
}

void FFT(int limit, Complex *a, int type) {
    if (limit == 1) return ; //只有一个常数项
    Complex a1[limit >> 1], a2[limit >> 1];
    for (int i = 0; i <= limit; i += 2) //根据下标的奇偶性分类
        a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
    FFT(limit >> 1, a1, type);
    FFT(limit >> 1, a2, type);
    Complex Wn = Complex(cos(2.0 * Pi / limit) , type * sin(2.0 * Pi / limit)), w = Complex(1, 0);
    //Wn为单位根，w表示幂
    for (int i = 0; i < (limit >> 1); i++, w = w * Wn) { //这里的w相当于公式中的k
        a[i] = a1[i] + w * a2[i];//左边加
        a[i + (limit >> 1)] = a1[i] - w * a2[i];//右边减
    }
}

int main() {
    int N = read(), M = read();
    for (int i = 0; i <= N; i++) a[i].x = read();
    for (int i = 0; i <= M; i++) b[i].x = read();
    int limit = 1; while (limit <= N + M) limit <<= 1;
    FFT(limit, a, 1);
    FFT(limit, b, 1);
    //后面的1表示要进行的变换是什么类型
    //1表示从系数变为点值
    //-1表示从点值变为系数
    //至于为什么这样是对的，可以参考一下c向量的推导过程，
    for (int i = 0; i <= limit; i++)
        a[i] = a[i] * b[i];
    FFT(limit, a, -1);
    for (int i = 0; i <= N + M; i++) printf("%d ", (int)(a[i].x / limit + 0.5)); //按照我们推倒的公式，这里还要除以n
    return 0;
}

但是这样写常数太大了，还需要一个很大的数组存，实测会T飞

2. 迭代版（蝴蝶变换）

所以我们引入一种迭代版，利用蝴蝶变换巧妙地实现FFT，使其真正成为$O(nlogn)$的高效算法。
在这里插入图片描述

然后下面就是FFT的迭代模板：

P3803 【模板】多项式乘法（FFT）

在这里插入图片描述

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

const int N = 5000007;

const double PI = acos(-1);

int n, m;
int res, ans[N];
int limit = 1;//
int L;//二进制的位数
int R[N];

inline int read()
{
    register int x = 0, f = 1;
    register char ch = getchar();
    while(ch < '0' || ch > '9') {if(ch == '-')f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar();}
    return x * f;
}

struct Complex
{
    double x, y;
    Complex (double x = 0, double y = 0) : x(x), y(y) { }
}a[N], b[N];

Complex operator * (Complex J, Complex Q) {
    //模长相乘，幅度相加
    return Complex(J.x * Q.x - J.y * Q.y, J.x * Q.y + J.y * Q.x);
}
Complex operator - (Complex J, Complex Q) {
    return Complex(J.x - Q.x, J.y - Q.y);
}
Complex operator + (Complex J, Complex Q) {
    return Complex(J.x + Q.x, J.y + Q.y);
}

void FFT(Complex * A, int type)
{
    for(int i = 0; i < limit; ++ i)
        if(i < R[i])
            swap(A[i], A[R[i]]);
        //i小于R[i]时才交换，防止同一个元素交换两次，回到它原来的位置。

    //从底层往上合并
    for(int mid = 1; mid < limit; mid <<= 1) {
        //待合并区间长度的一半，最开始是两个长度为1的序列合并,mid = 1;
        Complex wn(cos(PI / mid), type * sin(PI / mid));//单位根w_n^1;

        for(int len = mid << 1, pos = 0; pos < limit; pos += len) {
            //len是区间的长度，pos是当前的位置,也就是合并到了哪一位
            Complex w(1, 0);//幂,一直乘，得到平方，三次方...

            for(int k = 0; k < mid; ++ k, w = w * wn) {
                //只扫左半部分，蝴蝶变换得到右半部分的答案,w 为 w_n^k
                Complex x = A[pos + k];//左半部分
                Complex y = w * A[pos + mid + k];//右半部分
                A[pos + k] = x + y;//左边加
                A[pos + mid + k] = x - y;//右边减
            }
        }
    }
    if(type == 1) return ;
    for(int i = 0; i <= limit; ++ i)
        a[i].x /= limit;
        //最后要除以limit也就是补成了2的整数幂的那个N，将点值转换为系数
        //（前面推过了点值与系数之间相除是N）
}

int main()
{
    n = read(), m = read();
    //读入多项式的每一项，保存在复数的实部
    for(int i = 0; i <= n; ++ i)
        a[i].x = read();
    for(int i = 0; i <= m; ++ i)
        b[i].x = read();
    while(limit <= n + m)
        limit <<= 1, L ++ ;
    //也可以写成：limit = 1 << int(log2(n + m) + 1); 
    // 补成2的整次幂，也就是N
    for(int i = 0; i < limit; ++ i)
        R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
    FFT(a, 1);//FFT 把a的系数表示转化为点值表示
    FFT(b, 1);//FFT 把b的系数表示转化为点值表示
    //计算两个系数表示法的多项式相乘后的点值表示
    for(int i = 0; i <= limit; ++ i)
        a[i] = a[i] * b[i];
    //对应项相乘，O(n)得到点值表示的多项式的解C，利用逆变换完成插值得到答案C的点值表示
    FFT(a, -1);

    for(int i = 0; i <= n + m; ++ i)
        //这里的 x 和 y 是 double 的 hhh
        printf("%d ", (int)(a[i].x + 0.5));//注意要+0.5，否则精度会有问题
}

3. “三步变两步”优化

设$a$和 $b$ 是实多项式，$F = a+bi$ ，则 $F^2 = a^2-b^2+2abi$ ，注意到我们要求的$ab$正是$F$ 虚部的一半。这样只需要两次FFT就可以求出结果。

所以我们可以把$b(x)$放到$a(x)$的虚部上去，求出$a(x)^2$
，然后把$a(x)$的虚部取出来除 $2$ 就是答案了

void FFT(Complex * A, int type)//FFT板子
{
    for(int i = 0; i < limit; ++ i)
        if(i < R[i])
            swap(A[i], A[R[i]]);

    for(int mid = 1; mid < limit; mid <<= 1) {
        Complex wn(cos(PI / mid), type * sin(PI / mid));

        for(int len = mid << 1, pos = 0; pos < limit; pos += len) {
            Complex w(1, 0);

            for(int k = 0; k < mid; ++ k, w = w * wn) {
                Complex x = A[pos + k];
                Complex y = w * A[pos + mid + k];
                A[pos + k] = x + y;
                A[pos + mid + k] = x - y;
            }
        }
    }
    if(type == 1) return ;
    for(int i = 0; i <= limit; ++ i)
        a[i].x /= limit, a[i].y /= limit;
}

int main()
{
    n = read(), m = read();
    for(int i = 0; i <= n; ++ i)
        a[i].x = read();
    for(int i = 0; i <= m; ++ i)
        a[i].y = read();//把b(x)放到a(x)的虚部上
    while(limit <= n + m)
        limit <<= 1, L ++ ;
    for(int i = 0; i < limit; ++ i)
        R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
    FFT(a, 1);
    for(int i = 0; i <= limit; ++ i)
        a[i] = a[i] * a[i];//求出a(x)^2
    FFT(a, -1);

    for(int i = 0; i <= n + m; ++ i)
        printf("%d ", (int)(a[i].y / 2 + 0.5)); 
        //虚部取出来除2，注意要+0.5，否则精度会有问题,这里的x和y都是double

}

十、例题

1. P1919 【模板】FFT快速傅里叶变换

题目大意：给你两个整数，a和b，求$a\times b$。其中$1≤a,b≤10^{1000000}$。

对于每一个 n 位的十进制数，我们都可以看做一个 n-1 次多项式 A，满足

$$A(x) =a_0+a_1 \times 10+a_2\times10^2 \cdots +a_{n-1}\times10^{n-1}$$

然后对于这两个非常大的数，我们就可以用FFT快速求解答案了。

不要忘了进位！
不要忘了要保证数位上的单调性！因为我们普通的FFT卷积时，高次项一定由低次项得到，放在这里也一样,所以我们要倒序存储。

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

const int N = 5000007;

const double PI = acos(-1);

int n, m;
int res, ans[N];
int AA, BB;
int Lim = 1;//
int L;//二进制的位数
int R[N];

inline int read()
{
    register int x = 0, f = 1;
    register char ch = getchar();
    while(ch < '0' || ch > '9') {if(ch == '-')f = -1;ch =getchar();}
    while(ch >= '0' && ch <= '9') {x = x * 1- + ch - '0';ch = getchar();}
    return x * f;
}

struct Complex
{
    double x, y;
    Complex (double x = 0, double y = 0) : x(x), y(y) { }
}A[N], B[N];
Complex operator * (Complex J, Complex Q) {
    //模长相乘，幅度相加
    return Complex(J.x * Q.x - J.y * Q.y, J.x * Q.y + J.y * Q.x);
}
Complex operator - (Complex J, Complex Q) {
    return Complex(J.x - Q.x, J.y - Q.y);
}
Complex operator + (Complex J, Complex Q) {
    return Complex(J.x + Q.x, J.y + Q.y);
}

string s1, s2;

inline void FFT(Complex *J, double type)
{
    for(int i = 0; i < Lim; ++ i) {
        if(i < R[i]) swap(J[i], J[R[i]]);
        //i小于R[i]时才交换，防止同一个元素交换两次，回到它原来的位置。
    }
    //从底层往上合并
    for(int mid = 1; mid < Lim; mid <<= 1) {//待合并区间长度的一半，最开始是两个长度为1的序列合并,mid = 1;
        Complex wn(cos(PI / mid), type * sin(PI / mid));//单位根w_n^i;
        for(int len = mid << 1, pos = 0; pos < Lim; pos += len) {
        //for(int pos = 0; pos < Lim; pos += (mid << 1)) {
            //len是区间的长度，pos是当前的位置,也就是合并到了哪一位
            Complex w(1, 0);//幂,一直乘，得到平方，三次方...
            for(int k = 0; k < mid; ++ k, w = w * wn) {
                //只扫左半部分，得到右半部分的答案,w 为 w_n^k
                Complex x = J[pos + k];//左半部分
                Complex y = w * J[pos + mid + k];//右半部分
                J[pos + k] = x + y;//蝴蝶变换
                J[pos + mid + k] = x - y;
            }
        }
    }
}

int cnt_a, cnt_b;

int main()
{
    cin >> s1 >> s2;
    n = s1.length();
    m = s2.length();
    //相当于x=10 的多项式
    //读入的数的每一位看成多项式的一项，保存在复数的实部
    for (int i = n - 1; i >= 0; -- i) A[cnt_a ++ ].x = s1[i] - 48;
    for (int i = m - 1; i >= 0; -- i) B[cnt_b ++ ].x = s2[i] - 48;
    while(Lim < n + m) Lim <<= 1, L ++ ;
    //Lim = 1 << int(log2(n + m) + 1); // 补成2的整次幂，这里补成了2的整次幂，所以最后输出答案的时候要除以Lim
    for (int i = 0; i <= Lim; ++ i) {
        //换成二进制序列
        R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
        // 在原序列中 i 与 i/2 的关系是 ： i可以看做是i/2的二进制上的每一位左移一位得来
        // 那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数
    }
    //FFT 把a的系数表示转化为点值表示
    FFT(A, 1);
    //FFT 把b的系数表示转化为点值表示
    FFT(B, 1);

    for (int i = 0; i <= Lim; ++ i) 
    //对应项相乘，O(n)得到点值表示的多项式的解C，利用逆变换完成插值得到答案C的点值表示
        A[i] = A[i] * B[i];
    //IFFT 把这个点值表示转化为系数表示
    FFT(A, -1);
    int tot = 0;
    //保存答案的每一位（注意进位）
    for (int i = 0; i <= Lim; ++ i) {
        //取实数四舍五入，此时虚数部分应当为0或由于浮点误差接近0
        ans[i] += (int) (A[i].x / Lim + 0.5);
        if(ans[i] >= 10) {
            ans[i + 1] += ans[i] / 10;
            ans[i] %= 10;
            Lim += (i == Lim);//进一位
        }
    }
    //删掉前导零
    while(!ans[Lim] && Lim >= 1) Lim -- ;
    Lim ++ ;
    //输出
    while(-- Lim >= 0) cout << ans[Lim];
    puts("");
    return 0;
}